追捕逃逸型微分對策問題的識別域判別

張 霞， 高 巖， 夏尊銓

（1.大連理工大學 數學科學學院，大連 116024；2.浙江財經學院東方學院 信息分院，海寧 314408；3.上海理工大學 管理學院，上海 200093）

1 問題的提出

微分對策理論是現代控制理論中的一個重要研究課題，也是對策論的一個重要分支.微分對策是指在局中人之間進行對策活動時要用到微分方程（組）來描述對策現象或規律的一種對策，是解決對抗與競爭問題的有力工具.微分對策理論的研究可追溯到20世紀40年代，當時因軍事上的需要，由Isaacs帶領的團隊研究了導彈對抗飛行器策略問題，以此為開端，微分對策的基本概念及理論相繼提出，最早的文獻見于Isaacs的《Differential Games》一書［1］.微分對策理論的進一步發展來自兩個方面：一是最優控制理論；二是對策論.從最優控制到微分對策可看作是從一方控制發展到雙方或多方控制；從對策論到微分對策，又可看作是從靜態的對策理論發展到動態的對策理論.因此，微分對策理論的研究對控制領域和對策論中問題的解決起著重要的作用［2］.而且隨著該理論的不斷發展，現在也被廣泛應用到科學研究、工程技術、交通運輸、航天航空、環境保護、經濟管理和市場競爭等許多方面［3－5］.

根據提法的不同，微分對策問題有多種形式.本文將考慮單目標兩人追捕逃逸型微分對策問題（pursuit－evasion games），它是由Isaacs最早提出并命名的.描述如下：

考慮兩控制變量的微分動力系統

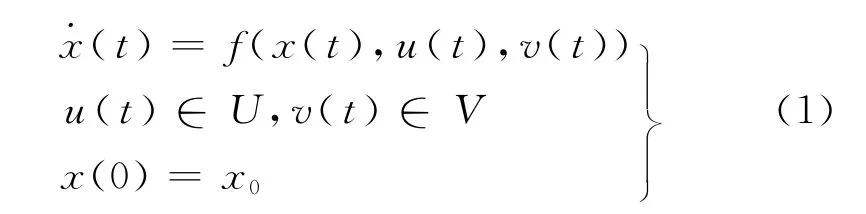
其中，x∈Rn是狀態變量；u∈U，v∈V是控制變量；U，V?Rm，f（x，u，v）為Rm＋n到Rm上的利普希茨函數.設Ω為Rn中開子集，也稱為目標.引入兩個局中人，第一個局中人為Ursula，控制變量為u，要使系統的狀態在有限時間內到達目標Ω；另一個局中人為Victor，控制變量為v，卻力爭使系統狀態永遠避開此目標Ω，這就是單目標兩人追捕逃逸型微分對策問題.

Krasovskii及Subbotin研究了追捕逃逸型微分對策問題的無優先規則的位置策略［2，6］，并證明了選擇定理.即在任何初始點x0，或者Ursula贏，或者Victor贏，二者擇一.然而，在Caratheodory意義下系統（1）無解，為此他們推廣了解的定義，給出了近似微分對策.與位置策略的研究方法不同，文獻［7］使用了無預見性策略（nonanticipative stragies），故局中人都可以通過對方行動的信息來決定自己的行動，這在現實中有很多應用事例.文獻［7］的另一個重要貢獻在于通過幾何方式去研究勝利域（victory domain，指無論對方如何行動，局中人都能贏的初始點的集合），據此可以繼續作勝利域的數值計算［8－9］.隨后又在文獻［10］中給出了具有狀態約束的追捕逃逸型問題，并證明了微分對策值的存在性.近期作者又將這一理論推廣到混雜系統［11］.

就具體應用問題來講，微分對策系統識別域（discriminating domain）的判別很重要，它直接關系到勝利域的表示以及微分對策問題的解.然而，正如對一般的非線性控制系統可生存性判別的充要條件很難具體使用一樣［12］，目前關于微分對策問題的識別域判別還沒有切實可行的判別準則.為此，本文參照文獻［13］的方法，研究了一類重要的控制系統即仿射非線性控制系統下的追捕逃逸型微分對策問題，給出該問題的系統識別域判別的方法，并結合凸可行問題的算法給出該判別問題的投影算法，最后給出這類微分對策問題的選擇定理.

2 識別域的判別方法

首先給出文中用到的幾個定義.

定義1K為Rn的閉子集，x∈K，若dK（x＋p）＝‖p‖，則稱向量p∈Rn為K在x處的近似法向量，所有p的集合記為NPK（x）.

定義2 若任意x∈D，任意p∈NPD（x），則稱D為f的識別域.Rn的閉子集K所包含的f的最大識別域稱為f的識別核，記作Discf（K）.

定義3 若任意x∈D，任意p∈NPD（x），則稱D為f的領導域（leadership domain）.Rn的閉子集K所包含的f的最大的領導域稱為f的領導核，記作Leadf（K）.

下面討論識別域的判別問題.考慮如下仿射非線性系統

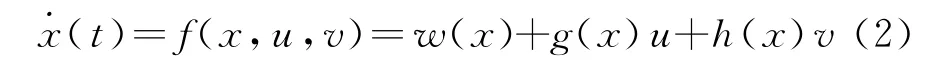
其中，w（x）為Rn到Rn的利普希茨函數，g（x）和h（x）為Rn到Rm＋n的利普希茨函數，u∈U為一度量緊空間.v∈V＝｛v∈Rm｜ai（v）≤0，i＝1，2，…，r｝，ai（v）為Rm上的凸函數.

定義區域

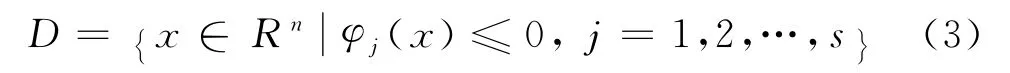
這里給定φj（x）為Rn上的連續可微函數.定義指標集

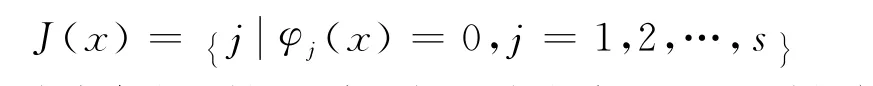
為方便問題的研究，在此給出本文所用到的假設條件及已知命題.

假設1

a.f（x，u，v）｜Rn×U×V→Rn為連續函數.

b.對任意u∈U，v∈V，f（·，u，v）為利普希茨連續.

假設2［14］存在y0∈Rn，使得φj（x）Ty0＜0，j＝1，2，…，s.

假設3［14］cl（γ（x））＝Γ（x）成立，其中

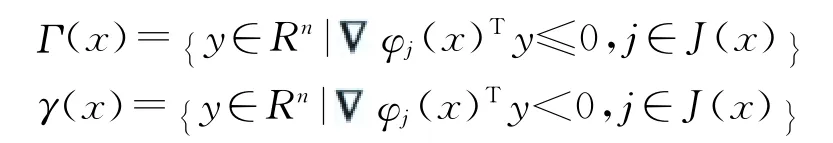
這里cl為閉包.

命題1［14］若假設2及假設3成立，則TD（x）＝Γ（x）.其中

命題2［15］若假設1成立，則D為f的識別域的充要條件是：

任意x∈D，任意u∈U，f（x，u，V）∩TD（x）≠φ其中為空集.

下面給出判別系統（2）的識別域的充分必要條件.

定理1 在假設1～3成立的條件下，區域D為系統（2）中f的識別域當且僅當不等式組

是相容的.其中，v∈Rm為變量.

證明 由命題1知，區域D為f的識別域的充要條件是：

任意x∈D，任意u∈U，f（x，u，V）∩TD（x）≠φ.當x屬于區域D的內部時，TD（x）＝Rn，定理顯然成立.因此只需考慮邊界點的情況，即集合.此時由命題1知，

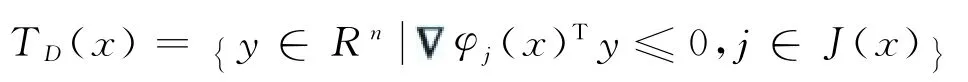
所以f（x，u，V）∩TD（x）≠φ等價于下面的不等式組有解

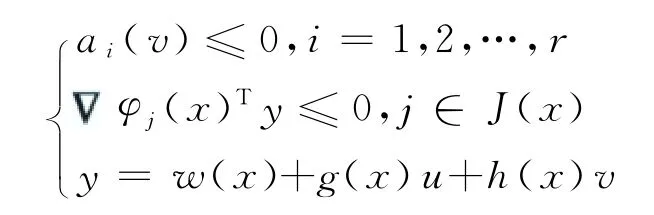
將y＝w（x）＋g（x）u＋h（x）v代入上面的第二個不等式，即得式（4a）和式（4b），證畢.

3 投影算法及選擇定理

下面給出判別系統（2）的識別域的算法.

因為式（4a）是關于變量v的線性不等式組，故可與式（4b）一起組成下面的凸不等式組

其中，v∈Rm為變量，q為式（4a）和式（4b）中全部不等式的個數.

判別該凸不等式組的相容性又可視為凸可行問題，令

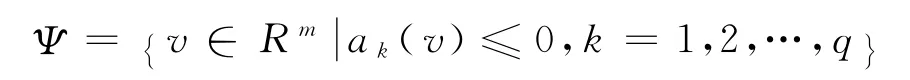
則問題轉化為尋找v∈Ψ.解決此問題的一個強有力的方法是投影算法［16］，下面給出判別識別域的投影算法.

Step 2i＝0，0＜η≤1，取v0∈Rm.

Step3 若點列｛vi｝收斂，則停止，x∈D為f的識別域中的點.否則轉至Step 4.

Step 4 計算σk∈?ak（vi）＝｛σk∈Rn｜z∈Rn，ak（z）≥ak（vi）＋［vi，z－vi］｝，

Θi＝｛y∈Rn｜ak（vi）＋〈σk，y－vi〉≤0，k＝1，2，

Step 5 選擇ωi｜η≤ωi≤2－η，計算vi＋1＝vi＋ωi（yi－vi）.

Step 6i＝i＋1，轉至Step 3.

定理2（收斂性） 在下列條件成立的情況下，算法收斂，即｛vi｝→v∈Ψ.

a.ai（v）≤0，i＝1，2，…，r為凸連續函數；

b.Ψ≠φ；

c.對任意v，?ai（v）是有界的，i＝1，2，…，r.

最后回到兩人追捕逃逸型微分對策問題，給出在仿射非線性系統下的選擇定理.

定理3 設f滿足假設1，令Ο＝Rn＼Ω，則Victor的勝利域為Discf（Ο），Ursula的勝利域為Ο＼Discf（Ο）.

證明 參照文獻［7］的選擇定理可以得到Victor的勝利域為Discf（Ο），Ursula的勝利域為Ο＼Leadf（Ο）.又因為f（x，u，v）＝w（x）＋g（x）u＋h（x）v，故

即Isaacs條件滿足，所以Leadf（Ο）＝Discf（Ο），故結論成立，證畢.

由此可見，在這種特殊情況下，局中兩人的勝利域瓜分了目標集的補集.而且該微分對策問題與無優先規則的位置策略相同，故只要知道系統的初始狀態，就能確定兩人的對策結局.

4 結 論

本文基于非光滑分析及生存理論得出了一類仿射非線性微分對策問題在不等式約束區域上系統識別域的判別方法，該方法可具體實現；并給出了算法，以及兩人追捕逃逸型微分對策問題的選擇定理.雖然微分對策理論的研究及應用有了極大的發展，但在追捕逃逸型微分對策模型的建立和求解以及不確定型微分對策等方面的研究尚不充分，這可作為進一步研究的課題.

［1］Isaacs R.Differential games［M］.New York：Wiley，1965.

［2］Krasovskii N N，Subbotin A I.Game theoretical control problems ［M ］. New York： Spring－Verlag，1988.

［3］Getz W M，Pachter M.Two－target pursuit－evasion differential games in the plane［J］.JOTA，1981，34 （3）：383－403.

［4］Zhu Q Y，Tembine H，Basar T.Hybrid risk－sensitive mean－field stochastic differential games with application to molecular biology［C］／／2011 50th IEEE Conference on Digital Object Identifier.Orlando，2011：4491－4497.

［5］Steffen J，Georges Z.Developments in differential game theory and numerical methods：economic and management applications［J］.Computational Management Science，2007，4（2）：159－181.

［6］Krasovskii N N，Subbotin A I.Universal optimal strategies in positional differential games ［J］.Differential Equat，1984，19（11）：1377－1382.

［7］Cardallaguet P.Differential game with two players and one target［J］.SIAM J Control and Optimization，1996，34（4）：1441－1460.

［8］Quincampoix M，Saint－pierre P.An algorithm for viability kernels in Holderian case：approximation by discrete viability kernels［J］.Journal of Math System，Estim and Control，1995，5（1）：115－118.

［9］Cardallaguet P，Quincampoix M，Saint－pierre P.Some algorithms for differential games with two－players and one target［J］.Mathematical Modeling and Numerical Analysis，1994，28（4）：441－461.

［10］Cardallaguet P，Quincampoix M，Saint－pierre P.Pursuit differential games with state constraints［J］.SIAM J Control and Optimization，2002，39（5）：1615－1632.

［11］Gao Y，Lygeros J， Quincampoix M. On the reachability problem for uncertain hybrid systems［J］.IEEE Transactions on Automatic Control，2007，52（9）：1572－1586.

［12］高巖.一類非線性控制系統可生存性判別［J］.信息與控制，2005，34（4）：510－512.

［13］高巖.仿射非線性控制系統生存性的判別［J］.控制理論與應用，2009，26（6）：654－656.

［14］Demyanov V F， Rubinov A M. Constructive nonsmooth analysis［M］.Berne：Peterlang，1995.

［15］Aubin J P.Viability theory［M］.Boston：Birkh?user，1992.

［16］Garcia－palomares U M.A superlinearly convergence projection algorithm for solving the convex inequality problem［J］.Operations Research Letter，1998，22（2／3）：97－103.