基于Kalman濾波器的衛星鐘差預報精度分析＊

劉建成，楊睿峰，徐 赟，王茂磊，桑懷勝

（北京環球信息應用開發中心，北京100094）

0 引 言

星地時間同步技術對衛星導航系統的導航、授時以及定位精度有著直接的影響。星地無線電雙向時間比對的工作原理是地面和衛星同時進行星地偽碼測距，根據兩組測距信息解算出衛星鐘相對于地面站基準鐘的鐘差。這種方法抵消了兩組測距共同的誤差，所以，鐘差測量精度很高。大多數實時導航用戶采用的是廣播星歷給出的鐘差，其精度將影響導航定位的精度，因此，研究星地無線電雙向時間比對體制下的衛星鐘差預報精度有著重要意義。

常用的鐘差預報方法包括最小二乘方法［1－2］、FIR 濾 波［1，3］、Kalman 濾 波［1，4－7］。 當 鐘 差 狀 態 模型是線性的，且狀態噪聲統計特性和測量噪聲統計特性已知時，Kalman濾波性能最優，Kalman濾波在鐘差預報方面獲得了越來越多的應用。對于Kalman濾波器，估計誤差方差隨著時間的遞推逐漸減小，直至達到穩態，此時估計誤差方差最小，在穩態條件下得到的預報誤差也最小，因此，穩態情況下的鐘差預報精度可作為分析星地時間同步性能的重要依據。

Meditch研究了衛星鐘差狀態噪聲為頻率白噪聲情況下的Kalman濾波器鐘差預報精度，利用Kalman濾波器狀態轉移矩陣得到了最小預報誤差的解析表達式［8］。Beisner研究了衛星鐘狀態噪聲為頻率白噪聲、頻率閃爍噪聲和頻率隨機游走噪聲且不考慮測量噪聲情況下的Wiener預測器的最小鐘差預報誤差，利用Wiener方法直接從頻域得到了比Meditch得到的更具有普適性的解析形式。目前，Kalman濾波器采用的鐘差狀態噪聲逐漸擴展到3階［9－11］，不但包括頻率白噪聲、頻率隨機游走噪聲，還包括頻率漂移隨機游走噪聲。研究鐘差狀態噪聲包括3階白噪聲且測量噪聲為白噪聲情況下的基于Kalman濾波器的衛星鐘差穩態精度。

根據Kalman濾波器達到穩態時的條件建立方程組，然后解該方程組，可以得到穩態解。該方法的優點是概念直觀，但當目標狀態變量增多時解方程組存在很大困難。通過消除Kalman遞歸形式中的增益項可得到預測協方差矩陣的遞歸公式，即Riccati方程，Vaughan解決了離散Riccati方程的非遞歸代數解問題［12］，利用這個結果可直接得到穩態解，繞開了解方程組的問題。在建立衛星鐘差的狀態方程和測量方程的基礎上，利用這種方法得到Kalman濾波器的穩態解，進一步得到預報誤差，建立起穩態情況下的鐘差預報誤差與衛星鐘狀態誤差、測量誤差及采樣時間間隔之間的解析關系，最后做了典型參數情況下的數值分析。

1 衛星鐘差Kalman濾波方程

采用3狀態衛星鐘差模型，包括相位、鐘速和頻率漂移值。考慮3類鐘差噪聲［10］，包括頻率白噪聲、頻率隨機游走噪聲和頻率漂移隨機游走噪聲。

若采樣時間間隔為T，衛星鐘差狀態向量為xk＝ ［a0a1a2］T，其中a0為鐘差，a1為鐘速，a2為頻率漂移量，那么建立多項式狀態方程為［10］

式中狀態轉移矩陣誤差矩陣為

式中q1、q2、q3分別為頻率白噪聲、頻率隨機游走噪聲和頻率漂移隨機游走噪聲的譜密度。

根據星地無線電雙向時間傳遞的原理，鐘差測量方程用xk表示為

從狀態方程和測量方程可以看出，兩者均為線性方程，則最優狀態估計就是卡爾曼濾波，其誤差協方差陣遞推過程為

穩態協方差矩陣?P定義為

式中:σ211為鐘差預測誤差方差；σ212為鐘差、鐘速預測誤差相關系數；σ213為鐘差、頻率漂移量預測誤差相關系數；σ222為鐘速預測誤差方差；σ223為鐘速、頻率漂移量預測誤差相關系數；σ233為頻率漂移量預測誤差方差。

2 衛星鐘差的穩態精度和預報精度

推導基于Kalman濾波器的衛星鐘差穩態精度，得到衛星鐘差預報誤差協方差陣與穩態協方差矩陣和衛星鐘狀態誤差矩陣的關系。

2．1 Kalman濾波器的穩態解

根據文獻［12］提出的離散Riccati方程的非遞歸代數解算法，構造矩陣

式中F、H、R、Q由式（1）和式（3）確定。

由于星鐘的系統模型為三階，所以Kf為6階特征值。若矩陣的特征值為λi（i＝1，2，3），則其對應的特征向量為

穩態解是S1＝λ1＋λ2＋λ3、S2＝λ1λ2＋λ2λ3＋λ3λ1和S3＝λ1λ2λ3的函數。下面說明如何確定S1、S2、S3．

矩陣Kf的特征方程為

由矩陣Kf的性質得到

式中λ1、λ2、λ3均為模大于1的特征值。

把式（11）展開，并與式（10）比較，得到

令S3＝x2，采用文獻［13］的做法，解上式方程組得到

式中的x是式（13）代入式（12）而得到的一元四次方程的解的最大值

從式（14）可以看出，基于Kalman濾波器的衛星鐘差穩態精度取決于參數q1、q2、q3、T、σ2．

2．2 衛星鐘差預報精度

假設Kalman濾波器開始預測工作前已經達

等式右端第一部分反映了Kalman濾波穩態誤差對預報精度的影響，取決于參數q1、q2、q3、T、N、σ2．第二部分反映了衛星鐘的狀態誤差對預報精度的影響，取決于參數q1、q2、q3、T、N．

如果定義間隔為T時的狀態噪聲矩陣函數為Q［T］，由式（2）確定，那么NT 預報誤差協方差陣還可表示為

式中NT衛星鐘差的預報誤差方差為σ211（N）＝P?N（1，1）．

當不考慮頻率隨機游走噪聲和頻率漂移隨機游走噪聲時，即q2＝q3＝0，此時β＝γ＝0，x＝到穩態，則鐘差參數預報初始誤差協方差陣為?P1＝?P．根據Kalman濾波器預測方程，預報誤差協方差陣的遞推關系為

根據此遞推關系，得到衛星鐘差狀態向量的N步預報誤差協方差陣，即衛星鐘差狀態向量的NT預報誤差協方差陣為度，再根據式（17）或（18）得到鐘差預報誤差方差，結果與文獻［8］一致。

3 數值分析

根據上面得出的理論結果，采樣時間間隔、偽碼距離測量誤差均方根對基于Kalman濾波器的鐘差穩態誤差均方根和鐘差預報誤差均方根的影響做了數值分析。數值分析采用的衛星鐘狀態誤差參數為［11］:q1＝1．11×10－22s2／s、q2＝2．22×10－32s2／s3、q3＝6．66×10－45s2／s5．

3．1 鐘差穩態精度與偽距測量精度的關系

分析了采樣時間間隔分別為5s、10s、15s時，基于Kalman濾波器的鐘差穩態誤差均方根隨偽距測量誤差均方根的變化關系，如圖1所示。從圖1可以看出，偽距測量誤差均方根越大，鐘差穩態誤差均方根就越大。采樣時間間隔越大，鐘差穩態誤差均方根就越大。因此，提高鐘差穩態精度的方法包括提高偽距測量精度和提高數據率。

3．2 鐘差預報精度與偽距測量精度的關系

圖1 鐘差穩態精度與偽距測量精度的關系曲線

分析了采樣時間間隔分別為5s、10s、15s時，基于Kalman濾波器的鐘差預報誤差均方根隨偽距測量誤差均方根的變化關系。1h和2h的鐘差預報誤差均方根與偽碼測量誤差均方根的關系曲線分別如圖2（a）和圖2（b）所示。

從圖2可以看出，偽距測量誤差均方根越大，鐘差預報誤差均方根就越大。采樣時間間隔越大，鐘差預報誤差均方根就越大。

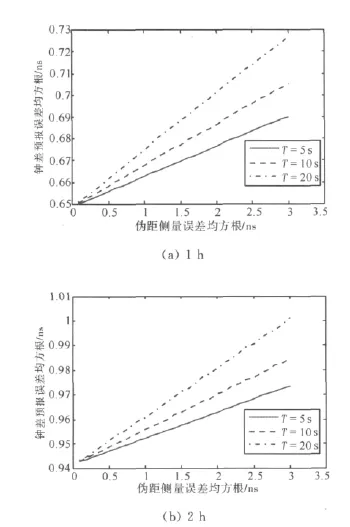
圖2 鐘差預報精度與偽距測量精度的關系曲線

4 結 論

研究了衛星鐘差包括3階白噪聲情況下的基于Kalman濾波器的衛星鐘差穩態精度。在建立衛星鐘差的狀態方程和測量方程的基礎上，利用離散Riccati方程的非遞歸代數解，得到了Kalman濾波器的穩態解，進一步得到了衛星鐘差預報誤差，建立起鐘差預報誤差與衛星鐘狀態誤差、測量誤差及采樣時間間隔之間的解析關系。做了典型參數情況下的數值分析。下一步的工作是分析衛星鐘的閃爍噪聲對基于Kalman濾波器的衛星鐘差預報精度的影響程度。

［1］ 劉 利．相對論時間比對理論與高精度時間同步技術［D］．鄭州:解放軍信息工程大學，2004．

［2］ DAVIS J A，HARRIS P M，et al．Least－squares analysis of two－way Satellite time and frequency Transfer Measurements［C］∥Proceedings of the 33thAnnual Precise Time and Time Interval（PTTI）Applications and Planning Meeting，Long Beach，California，USA，2001（11）:121－132．

［3］ SHMAL I Y，IBARRA－MANZHNO O．An optimal FIR filtering algorithm for a time error model of a precise clock［C］∥Proceedings of the 34thAnnual Precise Time and Time Interval（PTTI）Applications and Planning Meeting，Reston，Virginia，USA，2002（12）:53－68．

［4］ DAVIS J A，STACEY P W，et al．Combining time transfer measurements using a Kalman filter［C］∥Proceedings of the 34thAnnual Precise Time and Time Interval（PTTI）Applications and Planning Meeting，Reston，Virginia，USA，2002（12）:53－68．

［5］ DAVIS J A，GREENGHALL C A，STACEY P W．A Kalman filter clock algorithm for use in the presence of flicker frequency modulation noise［C］∥Proceedings of the 35thAnnual Precise Time and Time Interval（PTTI）Applications and Planning Meeting，Reston，Virginia，USA，2003（12）:53－68．

［6］ 陳小敏，李孝輝．基于自適應Kalman濾波器的原子鐘信號預測方法［J］．吉林大學學報·理學版，2009，47（3）:591－593．

［7］ GALLEANI L，TAVELLA P．Time and the Kalman filter－applications of optimal estimation to atomic timing［J］．IEEE control systems magazine，2010，30（4）:44－65．

［8］ BEUSMER H M．Clock error with a Wiener predic－tor and by numerical Calculation［J］．IEEE Transactions on Instrumentation and measurement，1980，29（2）:105－113．

［9］ HUTSELL S T，REID W G，GRUM J D，et al．Operational use of the Hadamard variance in GPS［C］∥Proceedings of the 28thAnnual Precise Time and Time Interval（PTTI）Applications and Planning Meeting，Reston，Virginia，USA，1996（12）:201－214．

［10］ HUTSELL S T．Relating the Hadamard variance to MCS Kalman filter clock estimation［C］∥Proceedings of the 27thAnnual Precise Time and Time Interval（PTTI）Applications and Planning Meeting，San Diego，California，USA，1995（12）:291－302．

［11］ HUTSELL S T．Fine tuning GPS clock estimation in the MCS［C］∥Proceedings of the 26thAnnual Precise Time and Time Interval（PTTI）Applications and Planning Meeting，Reston，Virginia，USA，1994（12）:63－74．

［12］ VAUGHAN D R．A non－recursive algebraic solution for the discrete riccati equation［J］．IEEE Transactions on Automatic Control，1970，15（1）:597－599．

［13］ RAMACHANDRA K V，MOHAN B R，GEETHA B R．A three－state Kalman tracker using position and rate measurements［J］．IEEE Transactions on Aerospace and Electronic Systems，1993，29（1）:215－222．