基于三角網格模型的剖面輪廓信息提取

張小青，吳坤華，黃 鶴

(1.福建水利電力職業技術學院水利工程系，福建永安366000;2.福建水利電力職業技術學院電氣工程系，福建永安366000;3.北京建筑工程學院測繪與城市空間信息學院，北京100044;4.現代城市測繪國家測繪地理信息局重點實驗室，北京100044)

基于三角網格模型的剖面輪廓信息提取

張小青1，吳坤華2，黃 鶴3，4

(1.福建水利電力職業技術學院水利工程系，福建永安366000;2.福建水利電力職業技術學院電氣工程系，福建永安366000;3.北京建筑工程學院測繪與城市空間信息學院，北京100044;4.現代城市測繪國家測繪地理信息局重點實驗室，北京100044)

為獲得三角網格模型的剖面輪廓信息，提出分層切片和鄰接排序算法。首先將模型中的三角形面片在剖切方向上分組;然后計算每一組三角形和剖切平面的交線，并按鄰接順序將交線按首尾順序連接;最后對每一層非封閉的輪廓線進行封閉處理，并計算剖面面積。試驗結果表明，該算法高效簡單，能夠有效地獲得封閉的剖面輪廓環。

三角網格模型;網格剖切;分層切片;鄰接順序;輪廓信息

一、引 言

三維模型中的三角網格模型具有許多良好的幾何特性，它能夠用多個面片逼近復雜形體的表面，而且容易處理，因此三角網格模型被廣泛應用于計算機圖形學、機械仿真、科學計算可視化等領域［1］。剖面輪廓線是三維模型的一個重要特征，它代表模型在某一位置處的大致輪廓和幾何形狀，并體現三維模型的基本外觀。如在文物三維展示和虛擬修復中，往往需要觀察其各個部位的截面特征，為達到既不損壞文物、又能夠觀察文物的截面形狀和大小的目的，可采用對三維模型進行剖切處理的方法實現文物剖面輪廓信息的提取。

目前常用的剖面輪廓線提取算法主要分兩類［2-4］：一類是先建立網格模型中的頂點、邊和三角面片的鄰接拓撲關系，再計算網格模型與剖切平面的交點，此類算法的優點是交點是有序的，但建立網格模型的完整的相鄰拓撲關系比較費時;另一類算法是根據網格模型中三角形的幾何特征，預先將三角形按特定法則進行排序和分組，并在每組中建立模型的點、邊和三角形面片的鄰接拓撲關系，再用平面對組中的三角形進行剖切處理。后一類算法只需比較每個小組中的三角形和剖切平面的位置關系，而在每個小組中建立網格模型中的頂點、邊和三角形之間的相鄰拓撲關系，減少了三角形面片和切割平面空間位置關系的判斷次數，簡化了網格模型拓撲關系的構建工作。

本文采用OBJ格式的三維模型數據，利用分層切片和鄰接排序算法，獲得了三角網格模型的剖面輪廓信息，并對其處理結果進行了分析。

二、輪廓線生成算法

本文的剖切算法可歸納為讀取模型數據，即先提取模型中的三角形頂點信息，將三角形在剖切方向上分組;然后在每一組中，比較三角形和剖切平面的空間位置關系，如果三角形和剖切平面相交，則將交線添加到交線組合中;最后對交線排序并進行封閉處理，獲得封閉的輪廓線。算法流程如圖1所示。

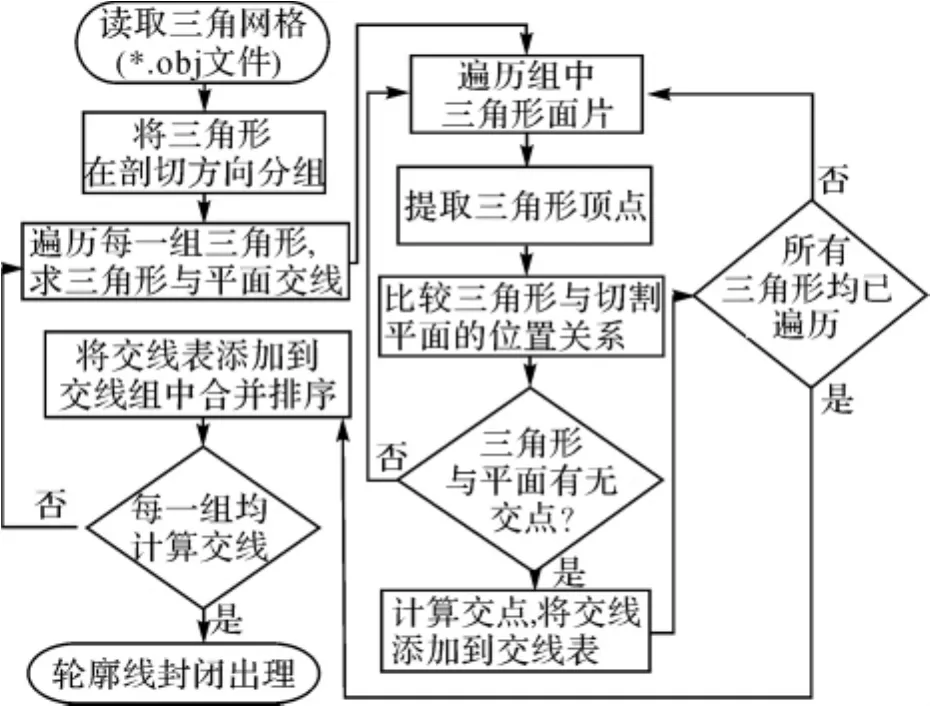
圖1 輪廓線生成算法流程

1.模型中的三角形面片分組

影響剖切算法效率的因素有兩個［2-4］：一個是模型中三角形的數量;另一個是剖切層數。為了提高算法效率，將模型中的三角面片進行預處理，即將模型中的三角形按照一定規則分成多個小組。本文是沿著Z軸方向剖切，即將模型中的三角形面片按其頂點坐標Z值的大小進行排序，求出網格模型中的Z坐標最小值Zmin和最大值Zmax，模型中的每個三角形面片被剖切的順序由該三角形的Z坐標最小值Zmin確定。假設剖切間距為d，Zi表示第i層剖切平面的高度，則第一層剖面的Z坐標為Z1，其值為模型中Z坐標最小值Zmin與剖切間距為d之和，第i層剖面高度的Z坐標為Zi，第i+1層剖面的Z坐標為Zi+1，相鄰剖面之間的計算公式為

Zi+1=Zi+d (1)

模型中三角形分組算法原理為：設Zi-1為第i-1層剖切平面的高度，Zi(i=1，2，…，n)為第i層剖切平面的高度，則存放在第i層剖切輪廓上的三角形面片由如下關系確定：當某個三角形的 Zmin和Zmax滿足公式：Zi-1≤Zmin＜Zi，而且Zmax≥Zi，則該三角形被分在第i個小組。

2.判斷三角形面片與剖切平面的位置關系

由于網格模型是由許多三角形構成的，因此模型與剖切平面的相交問題，可轉化為模型中的三角形與剖切平面的相交問題。圖2表示了網格模型與平面的相交情況，粗的多邊形線段表示相交線，將這3條相交線段順序連接，從而構成剖面輪廓多邊形。

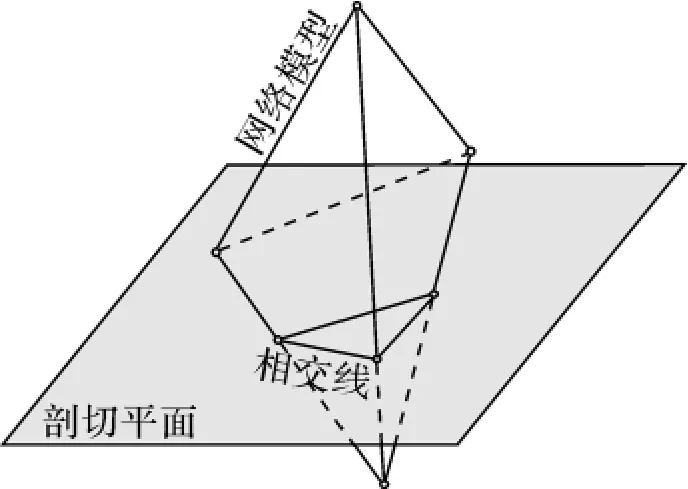
圖2 平面剖切網格模型

模型中的三角形和剖切平面是否有交點，可以通過計算三角形的每個頂點與平面的有符號距離，通過3個頂點的有符號距離，對剖切平面和模型中的三角形的位置關系進行判斷。三角形與剖切平面的空間位置關系，采用以下原則來進行判斷［6］：假設剖切平面方程為ax+by+cz+d=0，模型中的三角形的頂點P(X，Y，Z)到平面的有向距離為D，其值可表示為

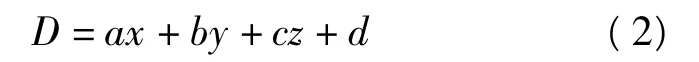
根據D值符號相同或不相同的情況，可確定三角形和平面的空間位置關系，包括5種情況，如圖3所示，除了圖3(a)中的三角形和平面沒有交點，圖3中(b)～(e)均存在交點。

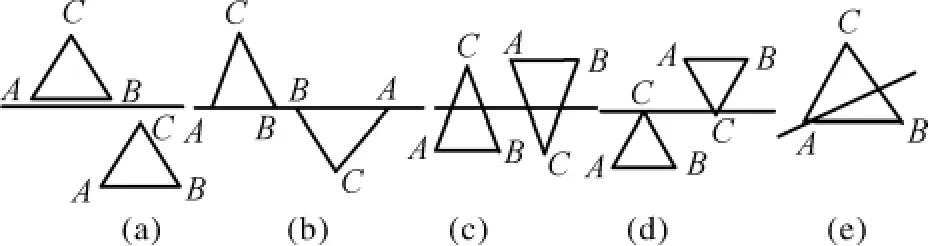
圖3 三角形和平面的相交情況

3.輪廓線封閉處理

獲得交線組合后，再對交線進行排序構建封閉輪廓環，先從交線組合中，任意取出一條交線，并將這條交線添加到一個新交線組合中，每條交線都有頭節點和尾節點。從這條交線的尾節點開始，尋找下一條交線上離這個尾節點距離最近的點，稱滿足要求的交線為相關線。由于這些交線都是同一層剖面上的交線，所以它們具有相同的Z坐標，判斷兩點的距離公式為

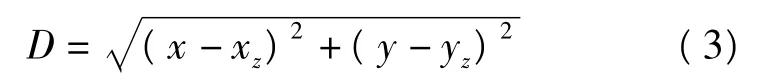
式中，(xz，yz)是取出的第一條交線的尾節點坐標。如果找到的最近點是相關線的頭節點，那么把這條交線添加到上述新交線組合中，并將這條相關線添加到前一條交線的后面;如果找到的最近點是相關線的尾節點，則將這相關線的頭節點和尾節點順序改變，同樣將這條已更改頭節點和尾節點順序的交線添加到上述新交線組合中。繼續上述算法，直至這層剖面的交線都添加到上述新交線組合中。

將交線排完順序后，要檢查每一組交線是否封閉。如果輪廓線不封閉［7］，則要進行封閉處理，在排完序的交線組合中，查找其尾節點是斷開的(即有斷點)某條交線，若找到這樣的交線，稱之為斷開線。首先計算該斷開線的斷點與其他交線(如果有多條斷開線)的斷點之間的距離，并將這些距離值進行比較，找到最小距離的那條斷線，這個最小距離值以D1表示，這條交線稱為相關線;然后計算該斷開線的終點與輪廓線中的起始線的起點之間的距離，令這個距離值為D2。輪廓線中的起始線是這樣的一條交線，即輪廓線是以這條交線的尾節點開始，并以這條交線的頭結點結束。如果距離值D1小于距離值D2，則在斷開線的尾節點和相關線的頭節點之間生成一條線;反之，則在斷開線和輪廓線的起始線之間生成一條線，令生成的那條線為輪廓線的起始線。繼續檢查是否有斷開線，若有，則繼續上述算法。最終得到一條正確封閉的輪廓線，并檢查輪廓線不相互交錯以及不通過原來的線條。

4.剖面面積計算

將每一層剖面輪廓線進行首尾排序之后，形成完整封閉的輪廓環，每一層輪廓環可構成簡單多邊形，對于由頂點A1、A2、…、An構成的簡單多邊形，令頂點Ai的坐標為(xi，yi，zi)(i=0，1，…，n)，由于該剖切方向是沿著Z軸，每一層的輪廓線具有相同的Z坐標，其面積計算公式為［8］

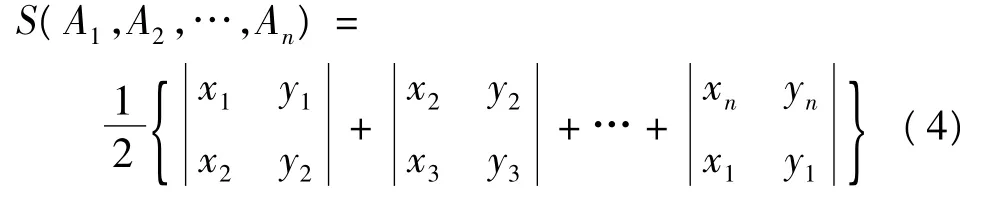
三、試驗結果與分析

本文采用的兔子網格模型如圖4所示，本文算法是在VC#2008環境下，調用OpenGL函數庫編程實現模型的顯示，將網格模型沿坐標軸Z軸方向剖切了11層，獲得每一層剖面輪廓線，進行排序構建首尾相連的輪廓線，并將未封閉的輪廓線進行封閉處理。如圖5所示，提取的是第8層剖面輪廓線，輪廓線中間有斷開，將其進行封閉處理之后，如圖6所示。得到封閉的剖面輪廓線。剖面輪廓線能很好地表達模型的幾何形狀，圖7為第8層剖面面積計算結果。

圖4 兔子網格模型

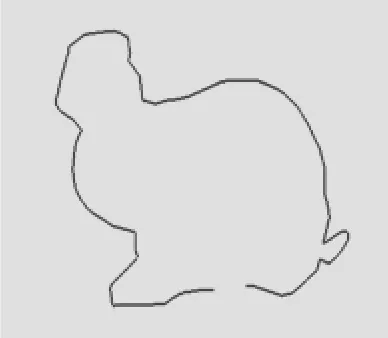
圖5 輪廓線封閉前

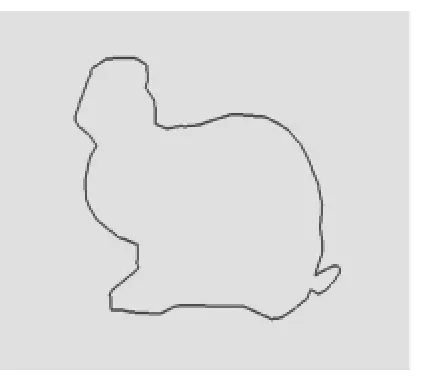
圖6 輪廓線封閉后

圖7 剖面面積計算

四、結束語

本文提出的剖切算法能對一些復雜或有拓撲錯誤的模型有很好的適用性。由于將模型中的三角形在剖切方向上進行了分組，減少了遍歷與剖切平面相交的三角形的次數，能夠很好地提高算法效率。利用交線的首尾節點拓撲關系對交線進行排序，而不需要對模型建立復雜的拓撲鄰接關系，利用最近距離法將輪廓線進行封閉處理，從而得到完整封閉的輪廓線。在計算機圖形學、機械仿真和文物三維展示等領域，往往需要觀察模型的內部或截面構造，這就需要通過剖切算法來提取剖面輪廓特征，輪廓線能夠很好地表現三維模型的剖面特征，因此，剖切算法具有重要的應用價值。

［1］ 張瑞，駱巖林，周明全，等.文物數字化的關鍵技術［J］.北京師范大學學報：自然科學版，2007，43 (2)：150-153.

［2］ 王靜亞，方亮，郝敬賓.STL模型特征面片自適應分層算法［J］.計算機應用研究，2011，28(6)：2361-2364.

［3］ 潘海鵬，周天瑞，朱根松，等.STL模型切片輪廓數據的生成算法研究［J］.中國機械工程，2007，18(17)：2076-2079.

［4］ 謝存禧，李仲陽，成曉陽.STL文件毗鄰關系的建立與切片算法研究［J］.華南理工大學學報：自然科學版，2000，28(3)：33-38.

［5］ 張小青，朱光，侯妙樂，等.基于四面體的不規則表面文物體積計算［J］.測繪通報，2011(10)：50-52.

［6］ VATANI M，RAHIMI A R，BRAZANDEH F，et al.An Enhanced SlicingAlgorithm UsingNearestDistance Analysis for Layer Manufacturing［J］.World Academy of Science， Engineering and Technology， 2009，49：721-726.

［7］ TOPCU O，TASCIOGˇLU Y，üNVER H ?.A Method for Slicing CAD Models in Binary STL Format∥6th International Advanced Technologies Symposium(IATS’11).Elazigˇ，Turkey：［s.n.］，2011.

［8］ 王泉德.任意三角網格模型體積的快速精確計算方法［J］.計算機工程與應用，2009，45(18)：32-34.

Extraction of Section Contour Information Based on Triangular Meshes

ZHANG Xiaoqing，WU Kunhua，HUANG He

0494-0911(2012)09-0026-03

P23

B

2012-04-25

張小青(1980—)，女，江西東鄉人，碩士，助教，主要研究方向為精密工程測量。