復系數奇異Sturm－Liouville方程的極限點判定

景海斌 鄧全才 岳崇山

(1.河北建筑工程學院，河北張家口075000;2.河北北方學院理學院，河北 張家口075000)

0 引言

其中p(t)=p1(t)+ip2(t)≠0，q(t)=q1(t)+iq2(t)是復值函數，w(t)是一個權函數，并在［0，+∞)上幾乎處處大于在［0，+∞)上局部可積，λ∈? 是一個譜參數.為表達方便，記早在1910年H.Weyl就對方程(1)為實系數的情形進行了討論，并給出了方程的一個分類:極限點型和極限圓型.若對任何λ∈?，方程(1)的任一解y∈，則稱方程為極限圓型，否則為極限點型.之后出現了許多關于極限點和極限圓的判別準則(如［1，p1552－1560］).對于復系數情況的討論開始于Sims的研究(見［2］)，之后B.M.Brown等人給出了方程(1)的Sims分類:極限點1型、極限點2型和極限圓型(見［3，定理2.1］).本文將給出方程(1)為極限點1型的判別準則.

1 Sims分類

1.1 預備知識

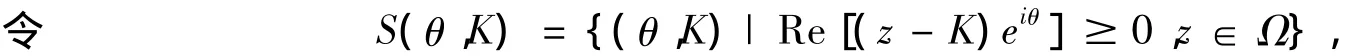
由此可定義半平面

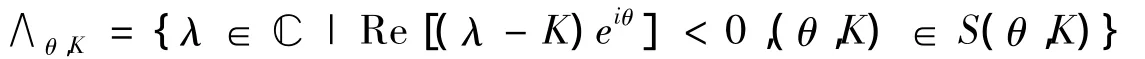
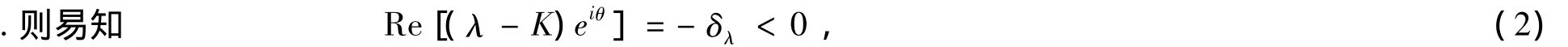
這里 δλ是 λ 到邊界 ? ∧θ，K的距離.易證對(θ，K)∈ (θ，K)，有

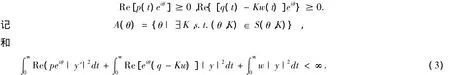
1.2 Sims分類

下面給出復系數奇異 Sturm－Liouville方程(1)的Sims分類(見［3，定理2.1］)，對λ ∈∧θ，K，方程(1)有三種情形可能出現:

1)(1)存在唯一的解滿足(3)，并且它也唯一屬于，此時稱方程(1)在∧θ，K上屬于極限點1型;

2)(1)存在唯一的解滿足(3)，但所有的解屬于，此時稱方程(1)在∧θ，K上屬于極限點2型;

3)(1)的所有解均滿足(3)，從而也都屬于，此時稱方程(1)在∧θ，K上屬于極限圓型.

注1 此分類與半平面∧θ，K有關，但利用常數變異法易證，若對某個λ0∈?，(1)的所有解均屬于，則對任意λ∈?，(1)的所有解均屬于，即極限點1型不依賴于∧θ，K.

2 極限點1的判別準則

為給出本文的主要結果，需用到下面的引理.

引理 設(θ，K)∈S(θ，K)，則對 λ ∈∧θ，K，方程(1)至少有一個非零解y(t，λ)滿足當t≥N時，有|pˉyy＇|＞l，其中N，l為大于零的常數.(見［4］，引理2)

定理1 若存在常數k1，使得p1(q1－k1w)≥0，p1≠0，且，則方程(1)是極限點1型的.

證明 不妨……