隧道圍巖滲透系數反饋分析

蔣 進 ，關勁松

（1.重慶交通大學，重慶 400042；2.遼源市東遼縣公路管理段，吉林 遼源 136200）

0 前言

巖土滲流有關參數的正確取用是滲流計算分析中的重要環節。數值計算或模擬試驗的精度再高，若選用參數不當也將導致計算分析結果的不可靠，而使確定的滲流控制方案不安全或過于浪費。目前計算機的精度已高達小數點后若干位，而參數選用中的誤差卻會高達數量級，這種計算中的精度失調問題實在應該引起注意。然而由于介質的復雜性，無論是實驗室試驗還是現場試驗，不僅需要花費大量的人力、物力和時間，而且往往得不到滿意的結果，造成大量的安全隱患。隨著數值解法和計算機的發展，使利用數學模型反求參數成為可能。

本文將針對這一事實專門闡述如何利用大型通用有限元計算軟件ANSYS的優化設計功能反饋分析滲透系數，使人們能夠根據已有經驗或研究成果對地質勘探資料和建筑材料性能做出比較可靠的估計，或者對取樣利用室內試驗設備測定及野外現場試驗測定取得的參數的準確性做出評價和修正以得到更可靠的有關參數。

1 滲流場與溫度場相似對比

滲流場中存在水頭梯度,水緩慢地從高水頭的地方流向低水頭的地方；同樣溫度場中的熱能在溫度梯度作用下從溫度高的地方向溫度低的地方傳導。 由此看來溫度場和滲流場的傳播過程具有較好的相似性，同時滲流與熱傳導的微分方程形式、控制變量，以及相關參數也具有很好的相似性，因此利用溫度場來模擬滲流場在理論上是具有可行性的。

1.1 控制方程的相似性

對于滲流，假定土體和水體是不可壓縮且介質均勻各項同性，則應用能力守恒定律可推導其控制方程為：

當溫度場中無熱源時，qgen=0,此時兩式各項相似，只是其物理意義有改變，T表示溫度而H表示水頭，k表示熱傳導系數和滲透系數。

1.2 模型的相似性

溫度場模型和滲流場模型相比擬，還應滿足幾何相似和邊界條件一致。

（1）幾何相似。溫度場模型的外部邊界應和所研究滲流區域的外部邊界在幾何上相似。當滲流區域為均質巖層時，則模型也應是均質的；當滲流區域是非均質巖層時,則要求模型中不同導熱介質的分界線應與非均質巖層的分界線亦保持相似，此時應注意滲流的微分控制方程有所改變。

（2）邊界條件一致。即溫度場模型的絕熱邊界與滲流區域的隔水邊界相對應。導熱邊界和透水邊界相對應，導熱邊界上的溫度則和透水邊界上的水頭相對應。

1.3 ANSYS單元理論相似

對于二維四節點矩形有限元單元，同1.2節中的分析，可以推導出其傳導矩陣為：

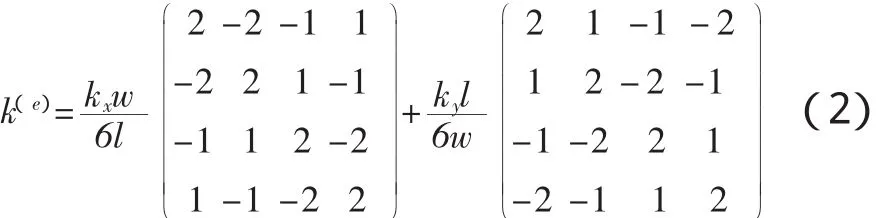
其中 C1=kx，C2=ky，C3=0，k 表示滲透系數。

對比滲流場和溫度場不難發現，其二維四節點矩形有限元單元的傳導矩陣的推到過程和結果都相同，這就更進一步表明，利用ansys溫度場，模擬滲流場是可行的。

2 滲透系數反演的實現方法

2.1 反演在ANSYS中的實現

2.1.1 何謂反演

所謂的反演就是預先根據經驗估計或現有的勘測結果確定各巖層的滲透系數，然后應用ANSYS求解滲透場的水頭分布，最后將求得的水頭值與相應的觀測值進行比較，并根據其差值和地質鉆孔資料來修改各巖層的輪廓和滲透系數，如此迭代，反復求解直至滿足精度要求為止。需特別說明的是，這種反求參數的方法并不能代替地質勘探工作，而僅僅只是水文地質工作的一個補充延續而已。其目的是為了減少人力物力的投入并且得到更準確的參數。

最后求得的自由面上的水頭值與相應的觀測值之間應滿足如下關系[2]：

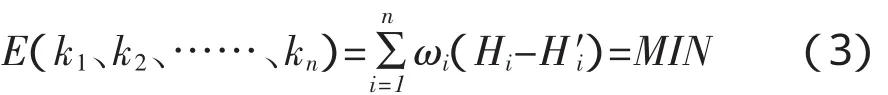
α≤k1≤β

式中，函數E稱為目標函數，ω為權因子，一般精度要求越高，相應的權因子值越大，H和H′，分別為節點水頭的求解值和觀測值，α、β分別為k的上限和下限。根據能量守恒定律可知，當各巖層的滲透系數滿足一定的比例條件時，線性方程組 [K][H]=[f]非唯一解，為消除這個不定解的因素，預先精確地給定某一巖層的滲透系數或由觀測資料給出滲流區域的滲流量。

2.1.2 迭代計算滲流自由面

滲流自由事先是不確定的，確定其位置是滲流計算的主要內容。滲流自由面上的水頭壓力等于大氣壓力，該面上任意一點水頭h等于該點的位置高程。為保證式（3）的解存在唯一解，在滲流自由面上應滿足條件：

對非穩定滲流自由面除應滿足式（4）外，還應滿足第二類邊界條件的流量補給關系，即按下式計算滲流自由面降下時由滲流自由面流入介質內的單寬流量q：

式中，μ為滲流自由面變動范圍內的介質有效孔隙率或給水度；θ為滲流自由面外法向與鉛錘線的夾角。

用有限單元法計算一個物理問題，它要求計算區域的邊界必須是完全確定的。然而隧道圍巖滲流是有自由面的無壓滲流，滲流自由面位置恰恰又是不確定的，滲流自由面位置是工程設計十分關心的問題，故需通過計算求出。滲流自由面需滿足式（4）的條件，這樣一來，滲流自由面位置需在計算中通過迭代來確定。迭代的計算步聚是[2]：

（1）首先根據滲流概念和經驗假定一條滲流自由面，以確定有限單元法的計算區域。

（2）將假定的滲流自由面作為第二類邊界，對于穩定的滲流由式 [K][H]=[f]計算出滲流自由面結點的水頭值h。

（3）比較假定滲流自由面結點的計算水頭值和其位置高程z視其是否滿足式（4）的條件。若不滿足，則用計算水頭值去改變結點的z坐標，形成新的假定滲流自由面，同時還確定了新的有限單元法計算的區域。反復上述計算步驟直至滲流自由面上的結點全部滿足給定的允許精度（|h-z|≤ε）。

在迭代過程中為了不改變網格的劃分和避免單元在壓縮或伸展的過程中出現畸形，可以采用丟棄單元（節點）的方法。即是當滲流自由面結點T的計算水頭值小于或等于其下結點的z坐標時，將T結點丟棄，改S結點為滲流自由面結點，形成新的有限單元法汁算區域，而與T結點有關的單元則不再參加計算。

2.2 ANSYS優化設計

ANSYS優化設計有兩種方法：第一種是通用的函數逼近優化方法[3]。這種方法的本質是采用最小二乘逼近，求取一個函數面來擬合解空間，然后再對函數面求極值。這種方法是一種普適的優化方法，不容易陷入局部極值點，但優化精度不是很高。另一種方法是對第一種方法的改進方法，叫做梯度尋優。如果說第一種方法是C0階、大范圍普適的粗優方法，那么第二種就是C1階、局部尋優的精優方法。一般來說，一個比較復雜的問題需要同時采用兩種優化方法，先用第一種初步求得優解的基本范圍，然后再采用第二種方法對優解的范圍進行更精確的確定。但是第二種方法不僅耗時間，而且還容易陷入局部最小點，因此通常的問題利用C0階函數逼近優化就足夠了。ANSYS中優化設計模塊有三大變量：（1）設計變量DV:即自變量。（2）狀態變量SV：用來體現優化的邊界條件，是設計變量的函數。（3）目標變量OBJ：最終的優化目的。它必須是設計變量的函數，而且只能求其最小值。概括說來ANSYS中實現優化設計的過程就是：在狀態變量SV的邊界條件下，在設計變量的取值范圍內不斷調整DV的取值組合，以使得目標函數OBJ逼近最小值。

3 滲透系數反演的工程實例

3.1 工程概況

為了驗證以上數學模型在ANSYS數值模擬環境中分析的準確性，以及在實際工程中實用性，現以八臺山隧道為實例，在ANSYS中進行結構分析。隧道處于巖體強風化帶、碎屑巖類的構造裂隙發育區、地表巖溶分布區為地下水的補給區，主要接受大氣降水的補給。

3.1.1 原始資料

根據原始資料，選取某斷面四組實測水頭值，其值如表1所列。

表1 實測水頭值統計表

3.1.2 模型參數

模型計算范圍選取埋深60m，隧道底部以下32m，軸線左右各60m，故整個模型為120m×100 m。左邊界水頭為64.8 m，右邊界水頭值為9.4 m（該值為相對值，相對于模型的原點）,采用ansys plane 55單元。該模型由于是反求隧道圍巖的滲透系數，所以沒有模擬襯砌和加固圈，并且由于實際計算中對超過三維的滲透系數進行反分析的理論還不成熟，而且工程當中又有一些滲透系數比較穩定，比較容易確定。例如襯砌的滲透系數，在實驗室中就可以比較準確地測定出來。顯然這類系數就沒有反演的必要性。另外為保證反分析解的唯一性，并且由于干燥狀態下圍巖的滲透系數對滲流量的影響很小，跟設計時的出入不大，所以選取其設計值，不參與優化設計，而作為優化結果的控制條件。具體的參數取值如表2所列，其中干燥狀態下的圍巖滲透系數為一個確定的值，而飽和狀態下的圍巖滲透系數為一個設計優化區域。

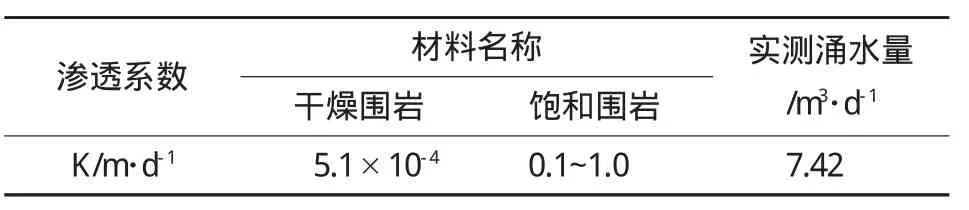
表2 滲透系數一覽表

3.2 優化設計

經過10次優化設計參數搜索最終得到10組優化設計組合，其中帶“*”號的為系統推薦的最優組合，最優設計又包含了33次迭代計算，并得最優組合*SET10*中涌水量為7.402 3m3/d,圍巖飽和滲透系數為0.451 79m/d。將ANSYS反演計算的結果和實際測量的結果對比可以得到以下數據和結論（見表3）。

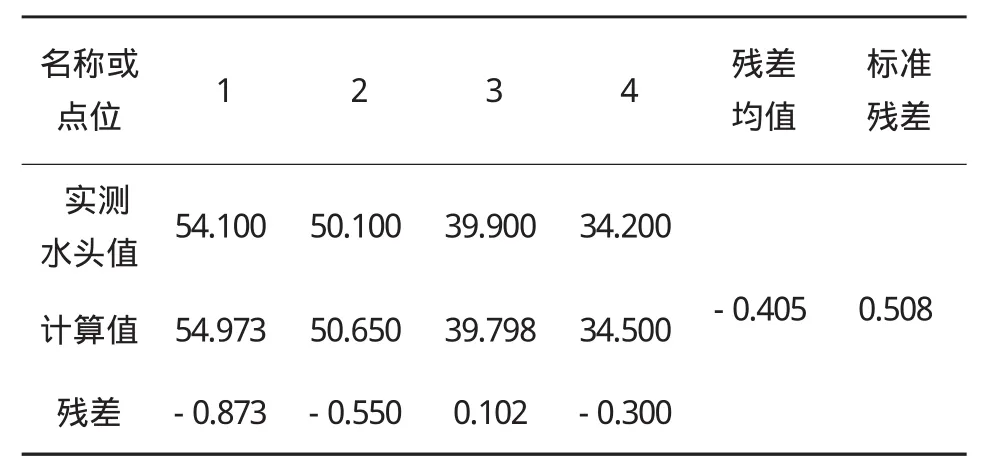
表3 ANSYS反演計算的結果和實測的結果對比表（單位：m）

由表3可以看出，隧道圍巖飽和滲透系數采用優化設計最優解時，計算水頭和實際勘測水頭相對殘差均值為-0.405，最大殘差為-0.873，而標準殘差為0.508，這說明計算水頭值與實測水頭值擬合很好，能夠滿足精度要求。另外狀態變量（涌水量）的計算值為7.406，而實測量為7.42，也表明了所求滲透系數的合理性。

4 結論及問題

通過ANSYS優化設計模塊，成功地反演出隧道圍巖的滲透系數，可以方便地檢驗實際勘測的滲透系數的準確性，在一定程度上減少了野外實驗在人力、物力方面的消耗。對同等地質條件下的工程提供了一個參考思路。雖然沒有對隧道加固圈進行分析，不過同樣提供解決加固圈厚度的有限元計算方法—優化設計，以加固圈厚度為設計變量，分析加固圈厚度與涌水量的關系，利用ANSYS溫度場模塊可以較好地實現對均勻介質滲流場的模擬。不過實際工程問題中，特別是巖體中是沒有均勻介質的，只有對模型做一定的簡化，才可以應用。該例正是因為隧道斷面處風化嚴重、巖層破碎厲害，并且沒有呈有規律方向的裂縫，所以才簡化為均勻介質。滲透系數的反演在一定程度上解決了在野外測定滲透系數的困難。本文在一定程度上說明了，可以利用ANSYS的溫度場求解滲流場的問題，不過由于滲流場介質的復雜性，在應用時還需考慮諸多因素對剛度矩陣的影響。ANSYS優化設計模塊的巧妙應用對實際工程來說，無論在安全上還是在經濟上都是大有益處的。

[1]王崧,劉麗娟，董春敏，等譯.有限元分析—ANSYS理論與應用（第三版）[M].北京：電子工業出版社，2011：296～316.

[2]毛昶熙.滲流計算分析與控制 (第二版)[M].北京：中國水力水電出版社，2003：306～316.