基于層次分析法的電力負荷組合預測

蔣 瓊 羅日成 劉從法 王菲菲 吳 瑩

（長沙理工大學電氣與信息工程學院，長沙 410076）

負荷預測是根據系統的運行特性、增容決策、自然條件與社會影響等諸多因素，在滿足一定精度要求的條件下，確定未來某特定時刻的負荷數據。負荷預測是電力系統經濟調度中的一項重要內容，是能量管理系統（EMS）的一個重要模塊[1]。

負荷預測的方法很多，因此如何選擇一種可靠又準確的方法是研究人員亟待解決的問題。目前國內外研究比較多的是組合預測法[2]。而且近年來組合預測法已經成為負荷預測領域中的一個重要的研究方向。但是利用層次分析法來求解組合預測的各單一負荷預測模型的相對權重的方法還不是很多。負荷的組合預測是對多種預測方法的預測結果進行分析、整合、判斷，最終確定預測的結果[3]。

層次分析法在20世紀90年代才躋身電力行業，其優勢就是將與決策問題有關的定性定量的因素進行綜合分析處理[4]。根據影響預測的因素來確定各方法的權重。將層次分析法的思想與組合預測的模型相結合更能有效的規避單一預測模型的缺點，利用單一預測模型的優點。

1 組合預測[5-7]

組合預測的原理：假設在某一預測問題中，某一預測的實際值為 yt(t=1，2，…，n)，而對該種問題有m種預測方法，其中利用第i種方法對t時段的預測值為fit。設各種預測方法的權重為W=(ω1，ω2，…，ωn，)T，并滿足組合預測的模型可表示為(t = 1,2,???,n )。

其主要思想是選取多個預測模型，按照某個標準(如預測有效度和殘差等)求取最優的組合權系數，將多個模型的預測結果進行擬合。

2 層次分析法（AHP）

層次分析法（Analytic Hierarchy Process，簡稱AHP）[8-9]是對一些較為復雜、較為模糊的問題作出決策的簡易方法，它把復雜問題分解成若干個組成因素，又將這些組成因素按支配關系分組形成遞階層次結構，通過兩兩比較得到各個因素的相對重要性。

層次分析法的一般步驟[6，10-11]：

1）明確方案目標，建立評價模型。該評價模型包括目標層、準則層和方案層，各層有若干因素組成。

2）構造比較矩陣。每一層中所含的各因素可以用上一層的一個因素作為比較準則來相互比較，當以上層某因素作為評價準則時，判斷矩陣A=(αij)n×n中的αij表示該層次中的第i個因素相對第j個因素的重要性，αij的取值一般取正整數1～9及其倒數， αij取值的規則如下表1所示。

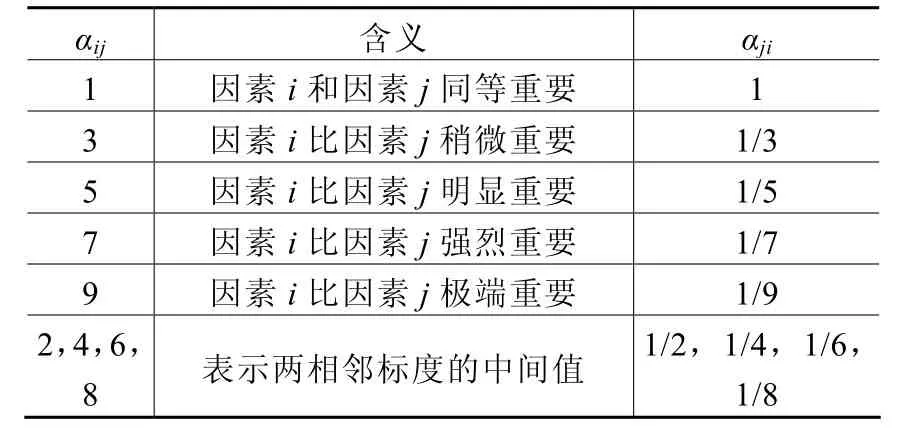
表1 比較矩陣取值[6，12]

3）求比較矩陣 A的最大特征值和最大特征向量ω，將ω歸一化之后ω'即為改層次因素的權重。

4）一致性檢驗。一致性檢驗的步驟：先計算一致性指標CI，CI=(λmax-n)/(n-1)；然后依據n查平均隨機一致性指標 RI；最后計算一致性比例CR=CI/RI，若CR＜0.10時，認為判斷矩陣的一致性是可以接受的，否則應對判斷矩陣作適當修正。

5）綜合各層次的權重，即可得到各方案對目標的權重。

3 電力負荷組合預測的層次模型

根據《國家電力公司電力市場分析預測內容深度要求》和各地區的負荷預測資料的收集，確定現階段影響負荷預測的指標主要有3個方面[13-15]：

1）歷史數據擬合度。每個地區的負荷發展在時間上有一定的規律性和相似性，各個預測模型首先要對歷史數據有較好的擬合程度。

2）經濟發展一致性。隨著改革開放，各地經濟相繼蓬勃發展，為滿足各地域企業對電力不斷增加的需求，電力負荷的供應也必須跟上國家經濟建設的發展速度，促進生產力的發展。經濟發展又可分為為GDP增長水平、第一產業增長水平、第二產業增長水平、第三產業增長水平、居民用電水平和用電方式調整等指標。這些指標均是影響中長期負荷發展的主要經濟因素，在負荷預測中要充分考慮。

3）政策因素。最近幾年，尤其是2011年，許多地區連續出現供電緊張，被迫拉閘限電的情況。除增加電源投資建設外，電價調整、加強政府與企業協調、優化需求側管理等政策因素也是解決這一問題的有效途徑。因此，在負荷預測中，政策因素不容忽略。

由電力負荷預測自身的特點，建立3層分析模型[14]。

目標層：本文中為所求的中長期負荷預測值。

準則層：該層次包括了實現目標所涉及的各級評價準則，本文包括3個元素：歷史數據的擬合度、經濟發展的一致性、政策因素。

方案層：該層提供了實現目標可供選擇的各種措施，決策方案等。本文采用了如下預測模型：包絡模型、指數平滑模型、移動平均模型、線性回歸模型，模型的層次結構圖如圖1所示。

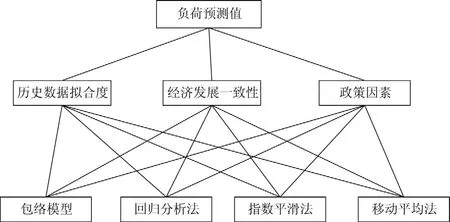
圖1 組合模型權重確定層次結構圖

4 某縣負荷預測算例

在對某縣 2005－2010年的除大用戶用電負荷進行負荷預測時選取了現在常用的幾種負荷預測模型，即包絡模型，指數平滑模型，移動平均模型，線性回歸模型。

1）某縣2005－2010年除大用戶用電負荷的實際數據和利用四種單一預測模型得到的預測值（見表2）

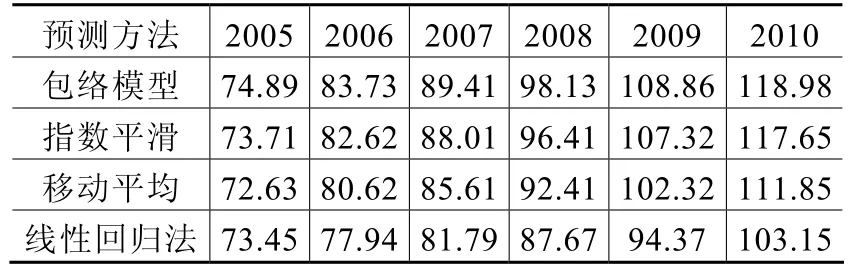
表2 各種預測方法對符合的預測結果 單位:MW

2）根據比較矩陣取值規則表1建立準則層對目標層的比較矩陣（見表3）

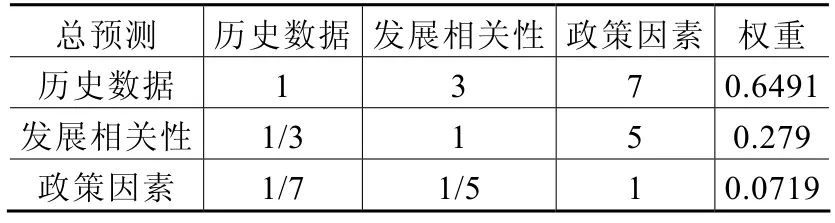
表3 準則層對目標層的比較矩陣和權重

利用Matlab[16]求解此比較矩陣的最大特征根對應的特征向量，歸一化后得出權重為[0.6491,0.279,0.0719]T。并驗證其滿足一致性要求。

3）同理可以建立方案層對準則層的比較矩陣（見表4－表6）

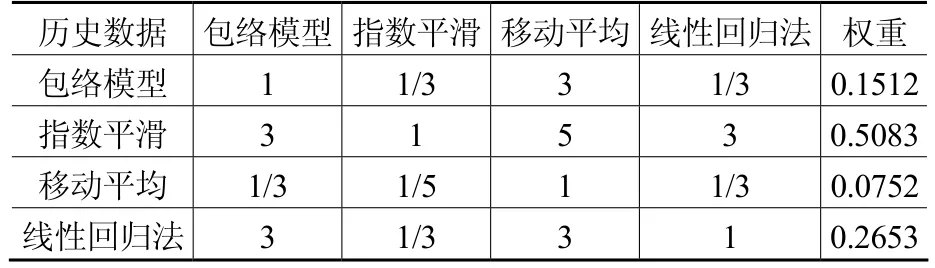
表4 歷史數據一致性準則下個單一預測模型的比較矩陣和權重

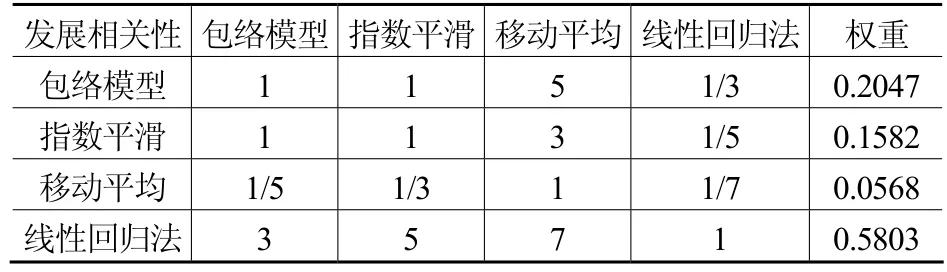
表5 發展相關性準則下個單一預測模型的比較矩陣和權重

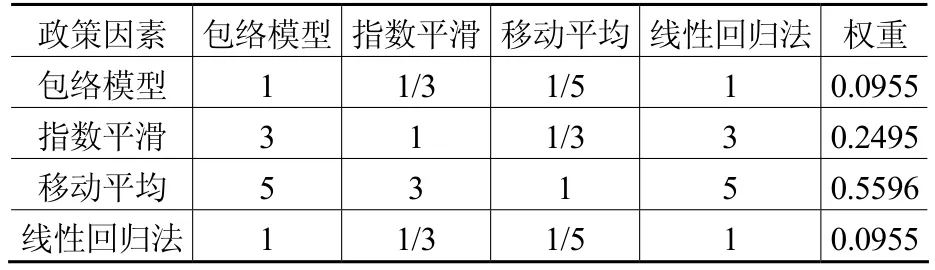
表6 政策因素準則下個單一預測模型的比較矩陣和權重

4）層次總排序

根據層次分析法（AHP）對權重的確定方法，把各單一預測模型對準則層的權重組合成方案層相對準則層的權重矩陣而準則層相對目標層的權重為 α=(0.6491,0.279,0.0719)則可得到各模型相對目標層的總排序為

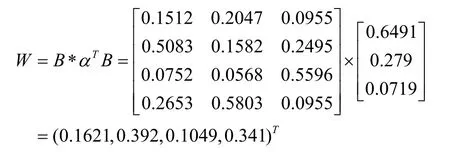
W 為個單一預測模型相對負荷預測的總得權重。以利用層次分析法求權重都通過了一致性檢驗。滿足一致性的要求。

表7 組合預測模型預測結果 單位:MW

5）組合預測模型和個單一預測模型優劣對比

各負荷預測的誤差由平均相對百分誤差[11]給出，相對誤差即絕對誤差所占真實值的百分比。相對誤差=|示值-標準值|/真實值。平均相對百分誤差為相對誤差的平均值得百分比。

各預測結果的平均相對誤差如表8所示。

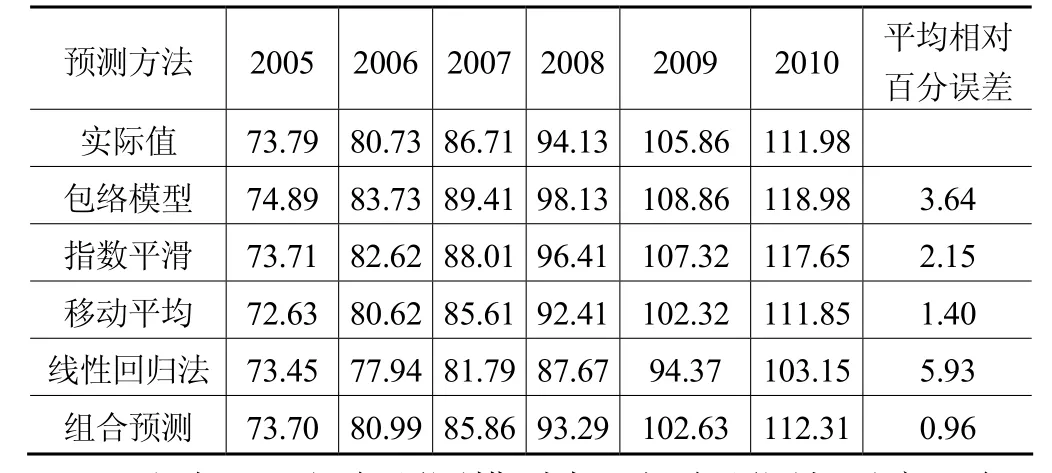
表8 預測結果和平均相對誤差 單位:MW，%

由表8可知各預測模型中，組合預測相對實際負荷的平均相對百分誤差最小，為 0.96%。算例分析結果表明，本文提出的方法有效提高了電網中長期負荷預測的精度。有效規避了個單一負荷預測的局限性。

5 結論

本文提出了基于層析分析法的中長期負荷預測組合預測的方法。構建了電力系統負荷預測的層次結構來確定各個單一負荷預測模型的相對權重。利用組合預測的理論求得負荷預測的最終結果，與其他單一負荷預測模型的預測結果進行對比，求其各自的平均相對百分誤差，比較出各種負荷預測的預測精確度，最后用某縣的除大用戶全社會用電負荷來進行算例分析，通過算例分析結果，表明本文提出的方法有效提高了電網中長期負荷總量預測的精度，所述方法在電力負荷預測中是一種有效的，實用的方法，具有一定的應用前景。

[1]唐卓貞.地方電網短期負荷預測的研究與實現[D].廣西大學,2008.

[2]孫林巖.組合預測方法及應用[J].預測,1990,4(9):31-35.

[3]原媛.電力負荷特性分析及中長期負荷預測方法研究[D].上海交通大學,2008.

[4]趙云飛,陳金富.層次分析法及其在電力系統中的應用[J].電力自動化設備, 2004,9(24):85-87.

[5]王蓮芬,許樹柏,層次分析法引論[M].北京:中國人民大學出版社,1990.

[6]劉賽,陳光東.層次分析法在電力負荷組合預測中的應用[J].長沙電力學院學報(自然科學版), 2002,4(17): 41-43.

[7]吉培榮,張玉文,趙青.組合預測方法在電力系統負荷預測中的應用[J]. 三峽大學學報(自然科學版),2005,5(27):388-400.

[8]黃文杰,傅礫,肖盛等.基于模糊層次分析法的風速短期預測組合模型[J].現代電力,2010,3(27):49-53.

[9]李春祥，牛東曉，孟麗敏.基于層次分析法和徑向基函數神經網絡的中長期負荷預測綜合模型[J].電網技術,2009,2(33).

[10]吳丹,程浩忠,夏夷等.基于模糊層次分析法的電力負荷組合預測[J].華東電力,2006,4(34):10-13.

[11]周湶,任海軍,李健等.層次結構下的中長期電力負荷變權組合預測方法[J].中國電機工程學報,2010,16(30):47-52.

[12]劉國興,劉啟盈,陳劍平.基于AHP負荷預測組合預測方法的權重確定[J].吉林電力,2008,3(196):12-17.

[13]趙希正.中國電力負荷特性分析與預測[M].北京:中國電力出版社,2002,1-17.

[14]吳丹,程浩忠,奚珣等.基于模糊層析分析法的年最大電力負荷預測[J].電力系統及其自動化學報 2007,1(19):55-59.

[15]孟祥萍,馮國杰,余雪芳等.模糊層次分析法在系統中長期負荷協調控制預測中的研究[J].長春工程學院學報(自然科學版),2010,3(11):38-41.

[16]李國勇.智能控制及其 Matlab實現[M].北京:電子工業出版社,2005.