數字鎖相技術在APFC電壓采樣中的應用

劉 攀，高艷霞，楊鄭浩

（上海大學，上海 200072）

1 引言

APFC（有源功率因數校正）技術采用全控開關器件構成開關電路對輸入電流波形進行控制，使其成為與電源電壓同相位的正弦波，徹底解決整流電路的諧波污染和功率因數低的問題。采用APFC技術能有效降低諧波含量，提高功率因數（功率因數能高達0.995），滿足嚴格的諧波標準，近年來得到廣泛的應用。單相有源功率因數校正電路結構簡單，克服了三相有源功率因數校正電路結構和控制復雜的缺點，電路易于實現，可靠性較高，廣泛應用于0.5-3kW范圍內單相輸入開關電源［1］。

傳統的APFC控制電路容易受到外電路的影響，電流環給定并非純正弦波，會導致功率因數降低，引入單相數字鎖相環技術對輸入電壓進行采樣以減小電流失真度，實現功率因數調節。

2 單相功率因數校正電路

基于平均電流法控制的單相APFC電路如圖1所示，主電路實際上由二極管整流電路和升壓斬波電路組成，控制電路采用雙閉環控制結構。外環電壓環以輸入整流電壓和輸出電壓誤差放大信號的乘積作為電流基準，內環電流環調節輸入電流平均值，使其與輸入整流電壓同相位且接近正弦波，校正功率因數［2］。

電流反饋網絡的采樣信號是Boost變換器的電感電流，正比于輸入電流的電流采樣信號與電流基準信號比較以后，其高頻分量的變化通過電流誤差放大器被平均化處理，放大后的平均電流誤差經信號處理（平均電流誤差與鋸齒波進行比較）轉換為PWM脈沖，控制開關管的開通和關斷。S導通時，電感電流線性上升。當輸入電流采樣信號與參考電流波形相交時，控制器控制S關斷，此時電感的自感電勢使二極管導通，儲能電感L通過二極管D對電容C進行充電，電感電流下降。通過對電感電流進行采樣和控制，使電感電流與輸入電壓同相位的正弦參考信號成正比，從而達到功率因數校正的目的［3］。

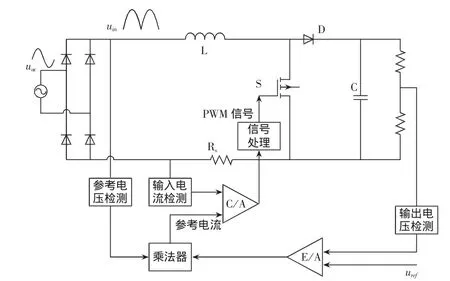
圖1 平均電流法控制的單相APFC原理框圖

Boost型APFC電路的狀態平均等效電路如圖2（a）所示，將電路中的電壓和電流用向量表示，可以得到圖2（b）所示的向量圖。由于輸入電壓是交流電壓整流后得到的直流脈動波形，是以［0，π］為周期重復的，因此輸入電壓表達式定義在［0，π］區間上。

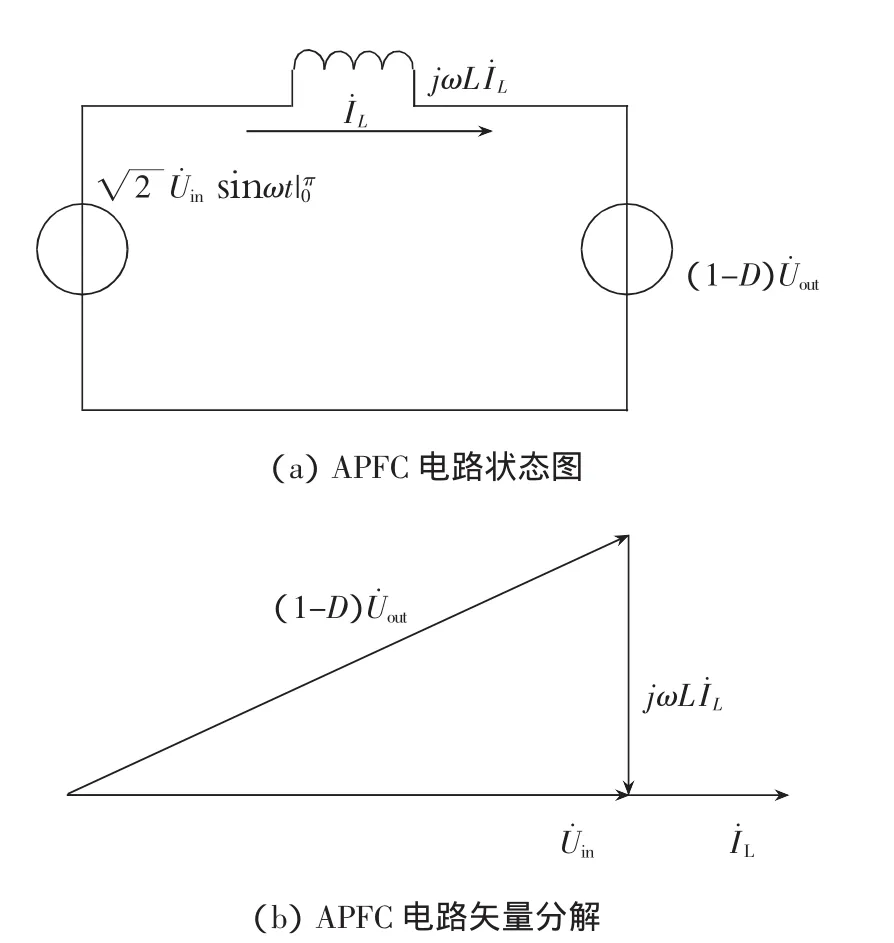
圖2 APFC電路狀態及矢量圖

U˙in為輸入電壓相量，I˙L為電感電流相量，電感兩端的電壓jωLI˙L超前電感電流90°，只要選擇合適的占空比控制規律，使（1-D）U˙out-U˙in＝jωLI˙L按正弦規律變化，且相位比U˙in超前90°，就可以實現電感電流對輸入電壓的跟蹤。

3 APFC電流波形畸變的原因

電網中理想的輸入電壓與輸入電流同相位，均為正弦波，分別為Iin_rmssin（ωt）。

其中uin經過整流橋整流后得到直流電壓，Uin_rms為輸入電壓的有效值，ω為輸入電壓的角頻率。若電壓、電流不同相位，設輸入電流為Iin_rmssin（ωt+θ），θ為輸入電流滯后于輸入電壓的滯后角。對輸入電流進行求導得到所需要的電流上升斜率：

變換器在輸入電壓過零附近時占空比值達到最大［4］，此時輸入電壓直接加在電感兩端（即電感電壓等于輸入電壓），則變換器提供的電感電流上升斜率為：

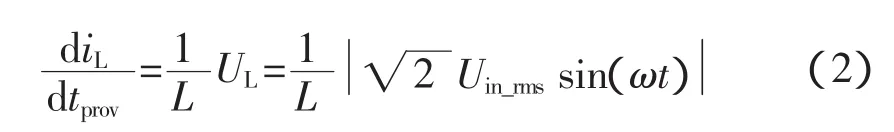
其中UL為電感電壓，電感電流等于輸入電流。變換器在輸入電壓過零時，電感電流的上升率很小，電感電流很難跟蹤上給定的基準電流，因此輸入電流發生畸變。

由式（1）和式（2）可以得出，電網角頻率 ω、輸入電流滯后角θ、電感L的大小及輸入電壓的波形都將對電壓過零時電流的畸變產生影響。其中電感越小，變換器提供的上升斜率越大［5］，電流畸變越嚴重。同時由于線路中耦合寄生感抗的影響，采樣輸入到AD端的輸入電壓并非正弦基波，若直接采用這種非正弦電壓作為輸入電壓，將導致電流環給定的電流基準為非正弦基波，影響PF值校正。

本設計引入數字鎖相環技術以濾除電網電壓中的各次諧波的干擾，抑制輸入電流過零點畸變，進一步提高功率因數。

4 數字鎖相環與濾波器設計

4.1 數字鎖相環建模

利用單相數字鎖相環對輸入市電進行鎖相，將鎖相后的電壓信號作為電壓相位給定值提供給電流環，以減少最高處的電壓畸變。單相鎖相環采用類似三相電壓鎖相環的方法，通過構造虛擬dq軸，PARK變換和應用數字濾波器，使電流環的電流基準信號跟隨輸入電壓變化。

圖3所示為靜止坐標軸與旋轉坐標軸的關系。

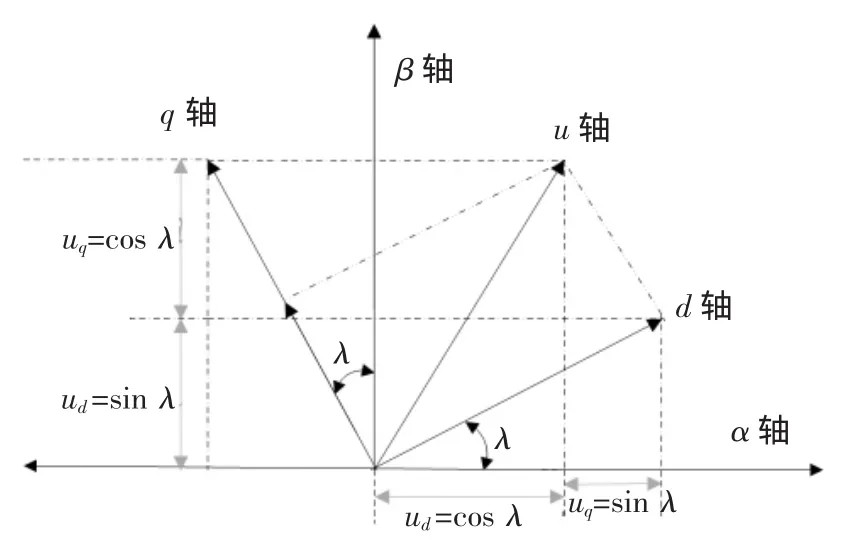
圖3 靜止／旋轉坐標軸空間關系

由上圖可以得出

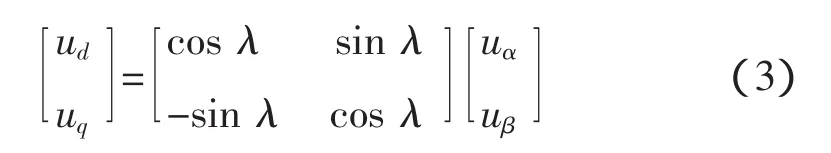
（其中α、β為靜止坐標軸，d、q為旋轉坐標軸，λ為兩坐標軸相位角）

將包含各次諧波的單相市電分解為基波與各相諧波之和，即

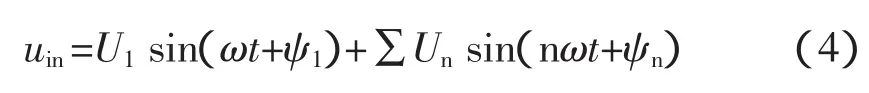
系統角頻率為ω，且dq旋轉坐標系同步旋轉。若基波相電壓在靜止坐標軸上投影為uα＝U1cos（ωt+ψ1）和 uβ＝U1sin（ωt+ψ1），則其在 dq 旋轉坐標系上的投影分別為 ud＝U1cos ψ1和 uq＝U1sin ψ1。

令所檢測的輸入電壓在當前靜止坐標系軸上的分量分別為：

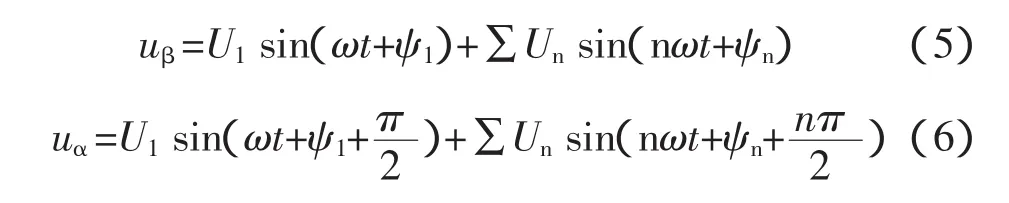
將式（5）、（6）代入式（3），經過 dq變換后得到：

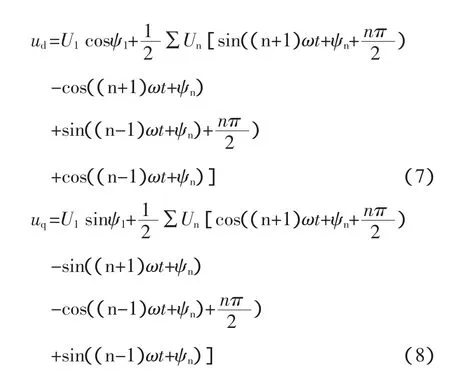
經高頻濾波后，得到兩個直流分量ud和uq，即ud＝U1cos ψ1和 uq＝U1sin ψ1。

設此處實際輸入角頻率為ω1，輸出角頻率為ω，則整個系統可以表示為：

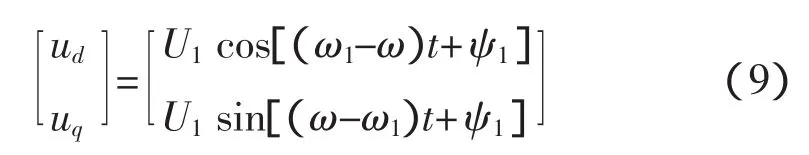
當輸出角頻率ω大于輸入角頻率ω1，通過PI調節使ω1-ω＝0，此時uq為直流量，直流量的輸入可以使輸出頻率加大，從而使輸出相位得到調整。當ω1≠ω，uq為變化的交流量，此時系統進入角頻率調整階段，如此反復直到輸入信號與鎖相環完全同步。

通過Matlab／Simulink對上述模型進行仿真，圖4所示為仿真模型，圖5所示為仿真波形。由仿真波形可以看出，利用鎖相環可以對輸入電壓完成鎖相，在仿真開始時（第一個周期時），鎖相電壓并不能完全跟隨實際輸入電壓，隨著仿真的進行，在第二周期時，鎖相電壓已經能夠完全完成對實際輸入電壓的鎖相。仿真結果表明利用該方法能夠有效地鎖住輸入電壓的相位。

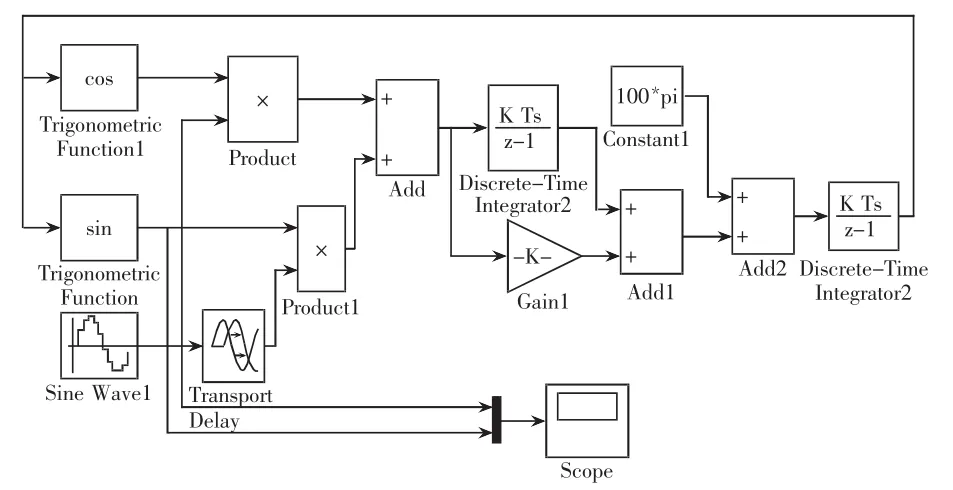
圖4 基于Simulink的數字鎖相環建模

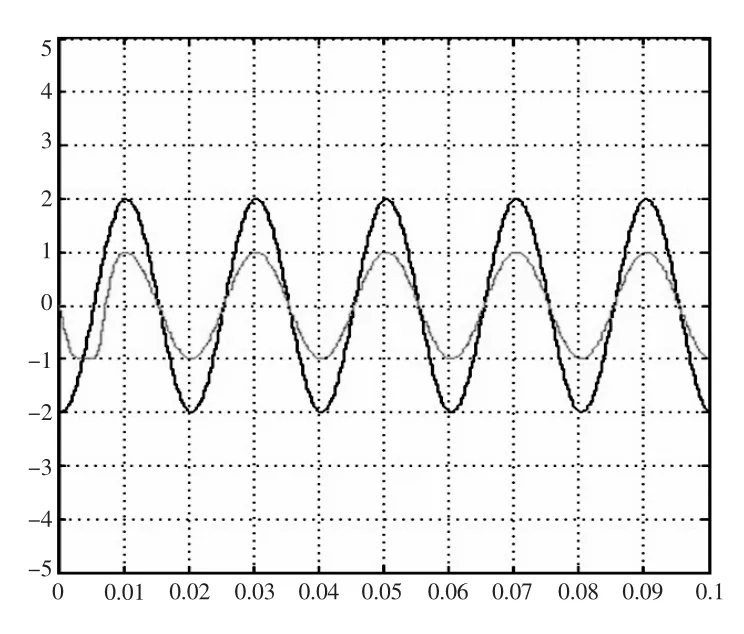
圖5 基于Simulink數字鎖相環仿真波形

4.2 數字濾波器設計

在鎖相環運算中，需要采用數字濾波器以濾除輸入電壓中的諧波分量。常用的低通數字濾波器采用一階結構，該方法容易造成相位延遲，且截止頻率越低，相位延遲越嚴重。本設計中的數字鎖相環需要濾除高于基波分量的各次諧波，市電基波頻率為50Hz，若使用一階低通濾波會造成較大的相位延遲，不能滿足系統要求。

采用巴特沃斯濾波器作為uq的數字濾波器，巴特沃斯濾波的特點是通頻帶的頻率響應曲線平滑，并且能夠保證衰減速度較快，效果優于傳統的一階低通濾波器。

為了方便數字巴特沃斯濾波器的設計，采用二階濾波設計方法，其轉移函數為：

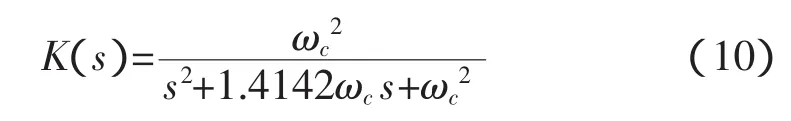
截止頻率為30Hz時計算得到截止角頻率為：

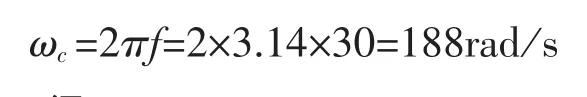
代入式（10）得：

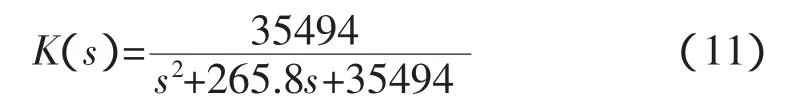
取采樣頻率為25.6kHz，對上式進行雙線性變換得到離散表達式：

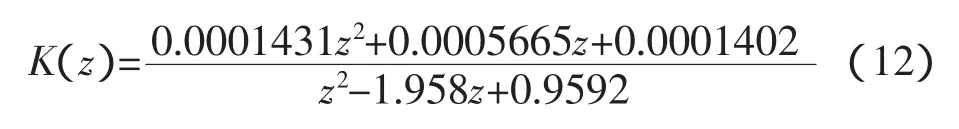
即為：

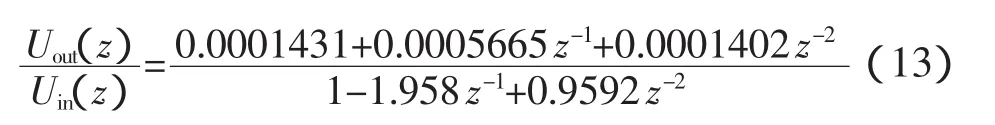
整理得到：

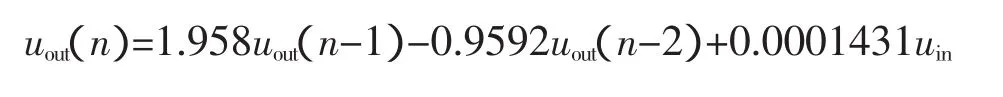
5 數字鎖相環實驗與分析

5.1 硬件設計

系統控制器采用TMS320F2812，該芯片A／D輸入為0-3.3V的電壓信號，故需將采樣得到的電網交流電壓信號轉化為0-3.3V的電壓信號。電壓轉換可以通過在采樣信號上疊加1.65V直流分量來實現，硬件電路如圖6所示。

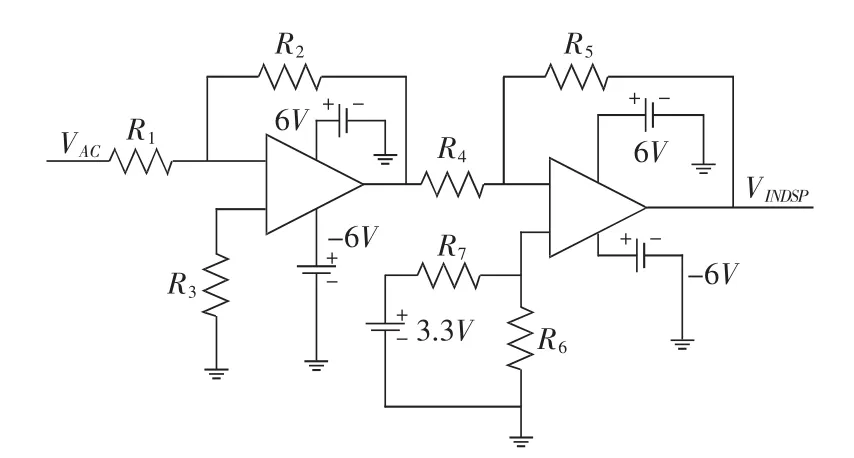
圖6 交流電壓采樣電路圖

由圖6得到輸入DSP2812的AD檢測口電壓為：

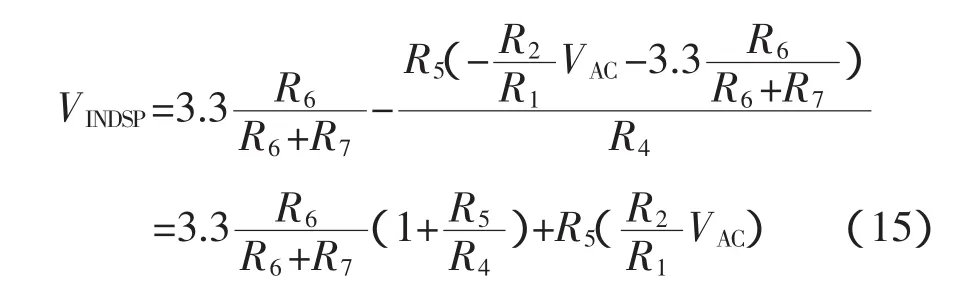
取 R1、R3、R5及 R6為 10kΩ，R2、R4、R7為20kΩ，則交流信號波形與經過處理的采樣波形如圖7所示，實驗波形符合上式計算結果。

將采樣處理后的電壓信號在數字信號處理器內完成異或功能，將第一位符號位進行邏輯變換，轉換為交流信號值存儲在寄存器中，處理原理如圖8所示。

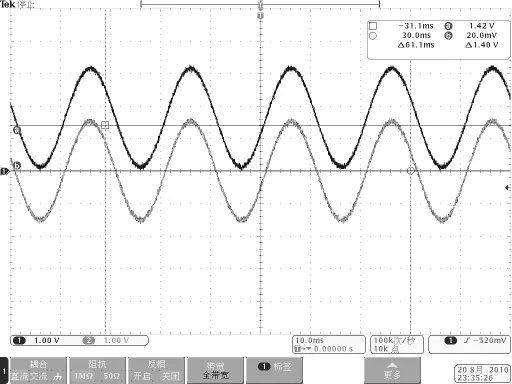
圖7 交流電壓信號采樣波形

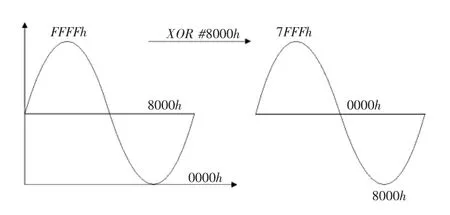
圖8 交直流信號在DSP內部邏輯運算圖

5.2 軟件設計

采用TMS320F2812數字信號處理器實現數字鎖相環，在RAM中建立一個512個字節的數組用于存放數據。設定采樣電網電壓為正弦基波，將其保存在RAM中，并且將指針后移128位作為余弦量。將反饋的相位信號進行Q格式變換，以加快運算速度，同時根據設計的巴特沃斯數字濾波器完成對高頻分量進行濾除。圖9所示為數字鎖相環的軟件設計流程。

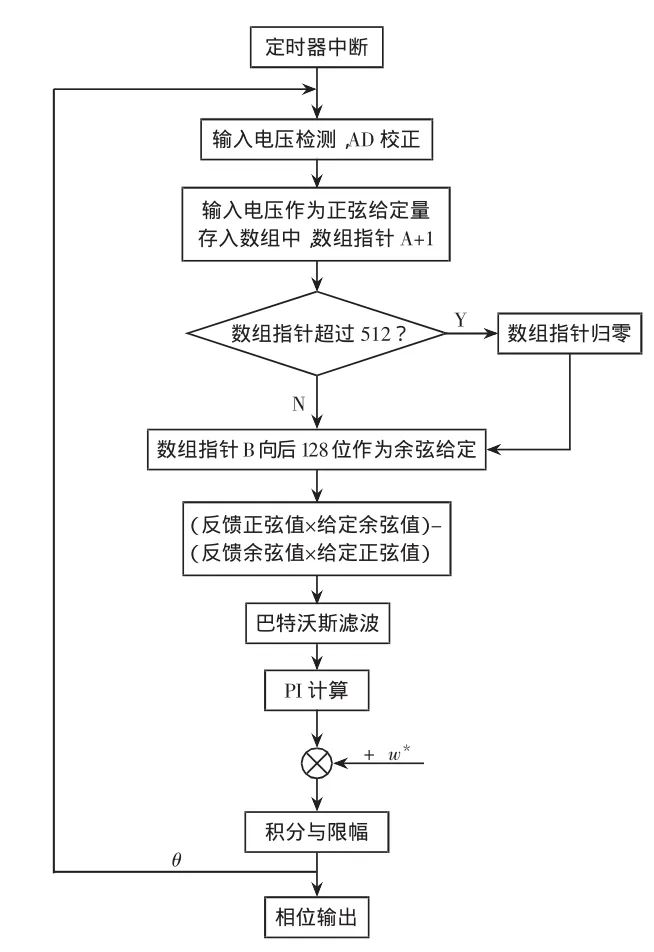
圖9 數字鎖相環軟件流程圖

5.3 實驗結果

采用數字信號處理器完成數字鎖相環設計，完成對輸入電壓的鎖相，從DSP編譯環境Watch Window中觀察實驗波形如圖10、11所示。圖10為未加入鎖相環時輸入電壓的波形，由于寄生參數及采樣偏差的影響，采樣得到的輸入電壓中存在諧波影響。圖11為加入鎖相環后的電壓采樣波形，實驗結果表明數字鎖相環明顯改善了輸入電壓波形的畸變。

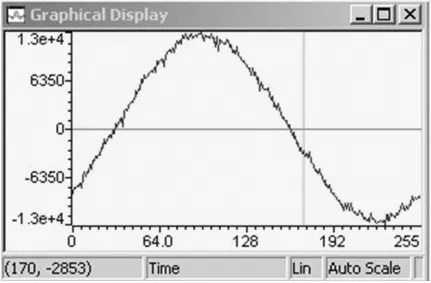
圖10 未加入鎖相環時輸入電壓的波形

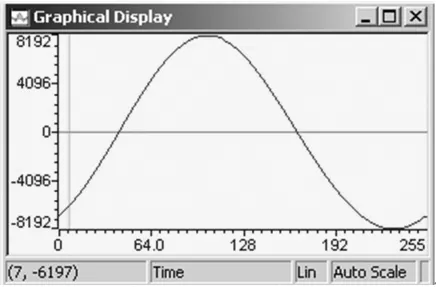
圖11 加入鎖相環后的電壓采樣波形

6 結論

在單相APFC原理基礎上分析了APFC電流畸變的原因，提出利用數字信號處理器TMS320F2812構建單相數字鎖相環，通過對輸入市電電壓完成鎖相以克服耦合寄生電感對功率因數校正的影響，解決輸入電壓過零時輸入電流過零畸變及峰值畸變問題。通過旋轉坐標系完成對數字鎖相環的建模，設計數字巴特沃斯濾波器濾除軸分量的高頻諧波，克服一階濾波器的相位延遲的不足。最后仿真和實驗結果表明利用數字鎖相環可以有效的完成對輸入電壓的鎖相，實現給定基準電流信號跟隨輸入電壓，實現功率因數校正。

［1］楊 旭，裴云慶，王兆安.開關電源技術［M］.北京：機械工業出版社，2004.

［2］魏 瀅，劉 輝.單相APFC數字控制的實現［J］.電源世界，2010，（1）：37-39.

［3］陳慶生.APFC技術在通信電源中的應用［J］.電源世界，2004，10：33-35.

［4］范 凱，謝少軍.單相PFC變換器的電流過零畸變問題研究［J］.電力電子技術，2009，43（4）：18-20.

［5］王菁，王毅，劉志宇.數字APFC的電流采樣算法改進［J］.電力電子技術，2009，43（5）：10-14.