基于矩陣束算法的極點提取分析*

徐 利， 鄒傳云， 陳 民， 何 毅

0 引言

從目標瞬態響應中提取其自然諧振復頻率即極點是現代目標識別的一種重要方法。極點提供了源無關特性，僅與散射體目標結構有關，因此目標極點準確提取是目標識別的關鍵所在。在眾多的極點提取方法如矩陣束算法(MPM，Matrix Pencil Method )[1-2]、Prony法、E脈沖法（E-pulse）中，由于矩陣束算法對噪聲具有較強的抑制能力和高精度的數據擬合能力而得到廣泛應用[3-6]。

極點提取的準確性受到目標極點模數、奇異值分解(SVD，Singular Value Decomposition)參數及噪聲的影響較大。為了提高極點提取精確度，結合實例，提出了目標極點模數及SVD參數的取值方法，并分析了不同信噪比情況下，噪聲信號極點提取的誤差。

1 矩陣束算法

根據極點展開法(SEM，Singularity Expansion Method)理論，目標電磁散射后時響應的數學模型可以表示成一系列衰減復指數和的形式：

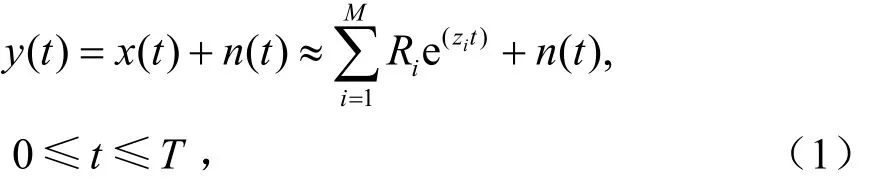
式中，x(t)為信號, n(t)為噪聲；Ri是復振幅（留數）；極點 zi=αi+jωi(αi、ωi分別代表衰減因子和角頻率)；M為極點個數。

為獲得最佳的 M , R和iz，首先由噪聲數據()ykt△(t△是采樣間隔，k為采樣點數)構造Hankel矩陣Y：

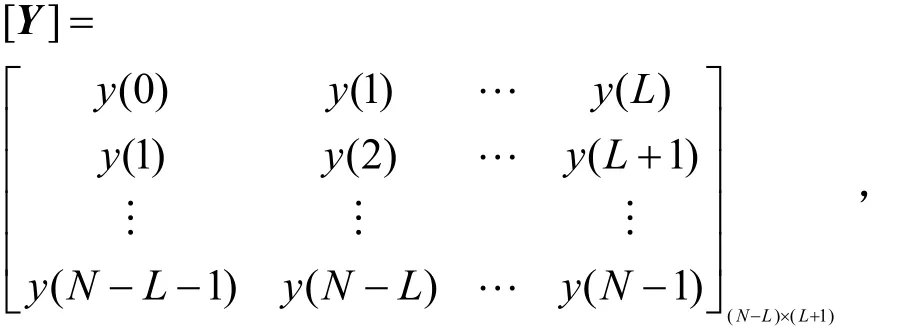
式中，N為數據采樣點數，L是函數束參數。

其次，對 Y進行奇異值分解[7]以獲得特征矢量及特征值：

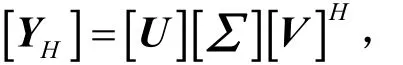
式中，矩陣U、V分別為Y的左奇異矩陣和右奇異矩陣，由矩陣 YHYHH、YHHYH的特征矢量組成，上標H表示共軛轉置。對角矩陣∑由Y的特征值組成。

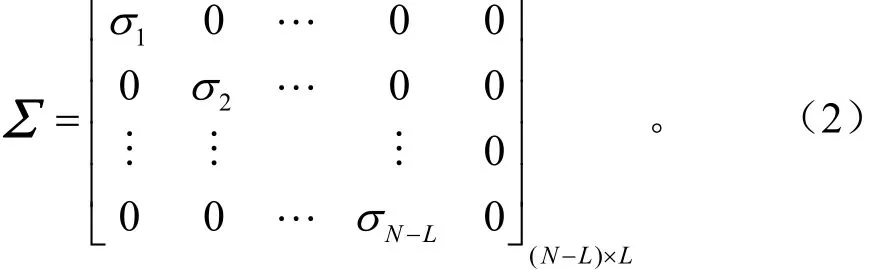
由于σc按照從大到小順序排列，比較每個σc和最大奇異值的比值直至滿足 σcσmax≈1 0-P(P代表計算精度，默認值為采樣數據的小數位數), 即可確定M的取值。

然后，構造濾波矩陣 V ′= ［ v1, v2,… ,vM］, 分別去掉 V ′的第一行和最后一行得到V2'，V1'，取∑的前M列 ∑ ′，則：

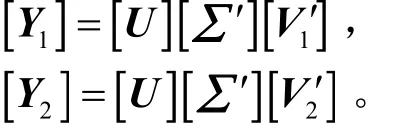
求得iM 和iZ后 ，系數iR可利用最小二乘法計算得到，具體式為：

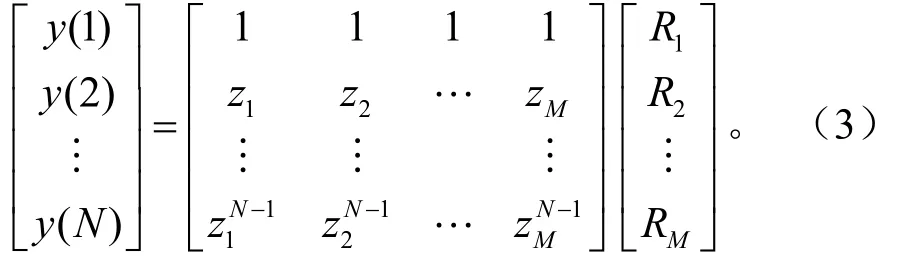
2 極點提取的參數選取

目標散射信號的極點不僅與噪聲有關，還受到M、P的影響。在一定噪聲范圍內，M、P的不同組合，使得提取的極點和真實極點之間存在較大偏差，而且還可能出現虛假、寄生極點。選擇正確的極點數M，才能利用奇異值分解改善極點提取效果[8]。

2.1 目標極點M可預知時，P的確定

首先，取P的默認值為起始值，以一定的步長減小 P，反復運行矩陣束算法，直到提取極點的個數與M相同為止，此時的P即為所求值。

為驗證方法的有效性，用3對留數、極點對{(11，1 ± 2 π × 2 j )，( 7 ejπ/2，2 ± 2 π × 3 j )，( 2 0ejπ，5±2π ×12j)}構造衰減指數和正弦信號，對應的時域信號如圖1所示。

對此衰減正弦信號加入20 dB的高斯白噪聲模擬噪聲信號。圖2 給出了具有3對極點的正弦衰減噪聲信號在P的不同取值時，極點分布情況。

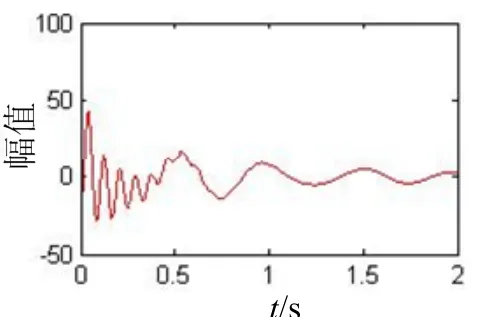
圖1 由極點、留數構造的正弦衰減信號

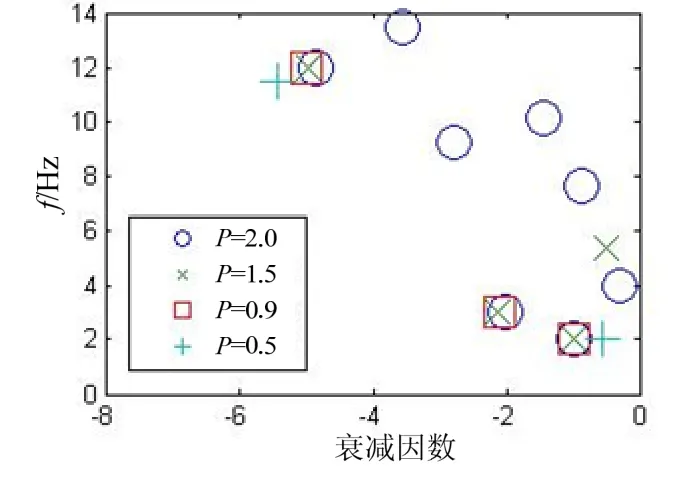
圖2 不同P值時，信號極點分布

由此可以看出，當P取0.9時提取的極點、留數值與所給參數值相同，證明了該方法的有效性。

2.2 目標極點未知時,M、P的確定

假設目標的極點個數為M。設置P由默認值開始，并以一定的步長遞減，利用矩陣束算法獲得目標不同M值時的極點、留數對(iZ,iR)；然后，利用極點、留數重構目標時域信號。定義歸一化均方誤差：

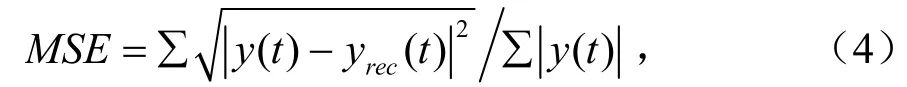
表征重構信號與原信號的誤差。在M的范圍內，通過遍歷求解MSE，其最小值對應的M即為目標極點個數。再選取與M對應的P值，即可獲得準確的極點、留數值。

以圖1所示的信號為目標信號，應用上述方法，獲得目標極點數M與MSE的關系，如圖3所示。

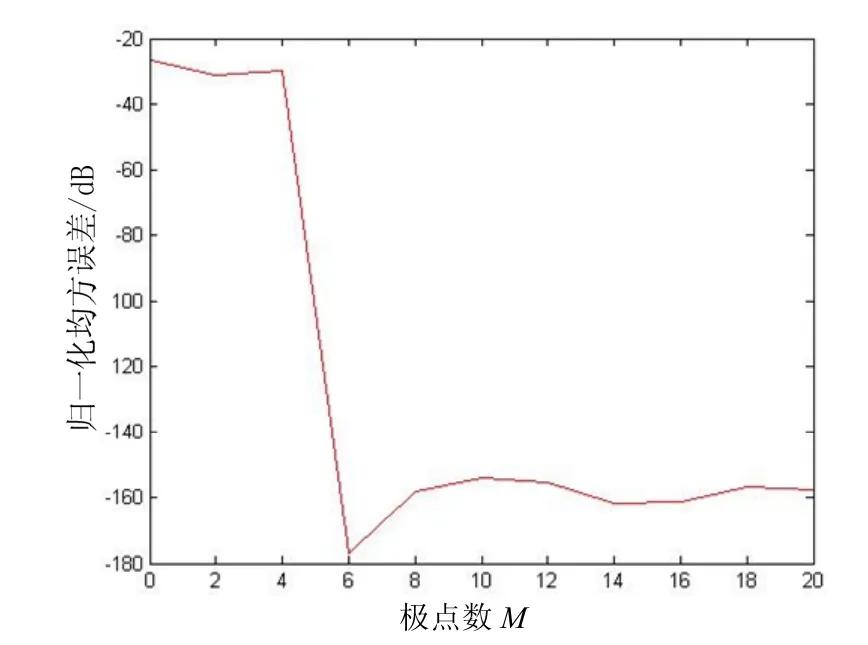
圖3 M與MSE的關系曲線

由圖3可以看出， MSE是M的函數，并且隨著M的增大而逐漸減小；當M為6時，MSE急劇衰減取得最小值；而后呈增大趨勢。由此表明，目標極點數目M可以確定為6。通過選取適當的P(此處為0.9)，可獲得精確的極點、留數值。

3 矩陣束算法抑制噪聲能力分析

矩陣束算法本身對噪聲具有一定的濾波作用，但是當信噪比超過一定的范圍時，目標極點提取準確性會產生較大的誤差。有些文獻給出了在確定的 P值下，實現極點精確提取的信噪比門限值為30 dB。但是對于不同的應用場合，如無芯標簽、基于極點特征的雷達目標識別，該門限值可以適當降低。

以圖1所示的信號為參考信號，分別對其加入SNR為40 dB，30 dB，20 dB，10 dB的高斯白噪聲，分析了不同 P 值情況下目標極點的分布及誤差分析，如圖4、表1所示。

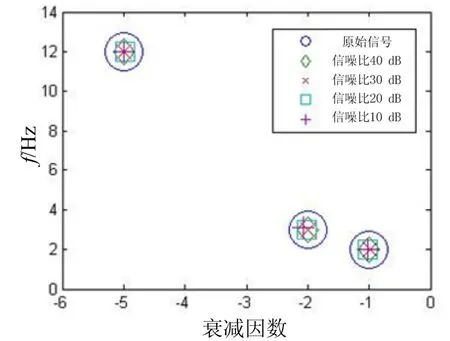
圖4 不同信噪比時，目標極點分布

圖4 表明，矩陣束算法在SNR為10 dB時，提取極點與原極點基本重合。表1給出了在該信噪比情況下，極點提取的數值分析。

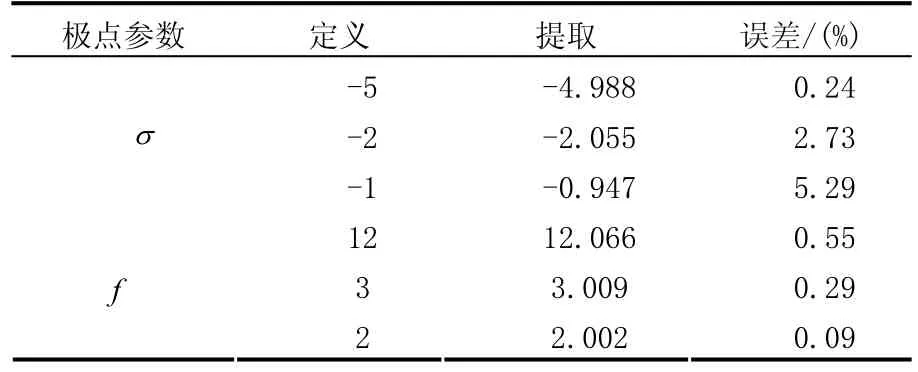
表1 SNR為10 dB時，提取極點的參數

由表1可以得出，在SNR為10 dB時，極點衰減因子σ和頻率f的最大誤差分別為5.29%、0.55%，表明矩陣束算法實現極點精確提取的噪聲門限值在10 dB時仍具有較高的可靠性。

4 結語

文中在矩陣束算法的基礎上分析了目標極點數目M以及SVD參數P對極點提取精度的影響，并提出了一種確定了M、P的取值方法。仿真結果表明該方法對實現極點準確提取的可行性，對基于目標極點提取的研究有重要的參考價值。

由于實際數據中不可避免的會伴有噪聲干擾，通過對不同信噪比的噪聲信號進行極點提取，分析了矩陣束算法抑制噪聲的能力，為矩陣束算法的應用指定了范圍。然而，10 dB的噪聲處理能力在某些方面可能會限制矩陣束算法的應用，以后的工作將著重研究對矩陣束算法的優化，以提高其對低信噪比信號的去噪能力。

[1] HUA Y, SARKAR T K. Matrix Pencil Method for Estimating Parameters of Exponentially Damped/undamped Sinusoids in Noise[J]. IEEE Trans.Acoustic Speech and Signal Processing, 1990,38(05)：814-824.

[2] SARKAR T K, PARK S, KOH J W, et a1. Application of the Matrix Pencil Method for Estimating the SEM(Singularity Expansion Method)Poles of Source—Free Transient Responses from Multiple Look Directions[J]. IEEE Trans on Antennas and Propagation，2000，48(04)：612-618．

[3] WANG S, GAUN X, WANG D et al. Application of Matrix Pencil Method for Estimating Natural Resonances of Scatters[J]. Electronics Letters, 2007, 43(01)：3-5.

[4] 蔡會甫，黃登山.一種高分辨穩定的相干信源 DOA估計[J]. 信息安全與通信保密, 2009(08)：47-49.

[5] 任淑婷，郭黎利. 基于模糊小波神經網絡的短波頻率預測[J]. 通信技術, 2011，44(04)：37-39.

[6] 李炎欣，賴惠成.一種新的小波域彩色圖像水印算法[J].通信技術, 2011，44(04)：129-131.

[7] 黃彩云,費耀平,李敏.基于奇異值分解的小波域水印算法[J]. 信息安全與通信保密, 2006(09)：133-135.

[8] LEE J H, KIM H T. Selection of Sampling Interval for Least Squares Prony Method[J]. Electron. Lett.,2005, 41(01)： 47-492.