調頻步進頻雷達中距離起點誤差分析

孫 林 田衛明 曾 濤

①(北京理工大學雷達技術研究所 北京 100081)

②(清華大學電子工程系 北京 100084)

1 引言

隨著雷達技術的進步和微波遙感應用的擴展，軍事偵察、地形測繪和微波遙感等領域對合成孔徑雷達分辨率要求越來越高。分辨率改善需要提高雷達信號帶寬，傳統雷達信號的產生一般采用直接數字頻率合成(DDS)技術直接產生寬帶信號的方式。直接產生寬帶信號的方法由于DDS工作時鐘頻率約束而受到限制。目前先進的超寬帶雷達的信號帶寬可達到GHz量級，而DDS技術難以在滿足超寬帶的同時保證信號質量。此外瞬時超寬帶信號對AD采樣速率和存儲帶寬也提出了較高要求。調頻步進頻信號是解決該問題的有效途徑，因此在高分辨雷達系統中獲得了廣泛應用，如德國的PAMIR[1,2]，法國的RAMSES雷達系統等都采用了調頻步進頻信號作為工作信號。

調頻步進頻體制在不增加瞬時帶寬的條件下提高了雷達的距離向分辨率，同時降低了雷達系統對采樣率的要求[3-6]。但是，調頻步進頻信號在脈沖壓縮處理后通常會出現柵瓣[7]。文獻[8,9]從模糊函數的角度分析了柵瓣出現的原因，提出了一種將柵瓣壓低到閾值高度以下的方法，并從壓低柵瓣的角度給出了調頻步進頻信號參數設計的建議。李海濱等人[10]提出了對調頻步進頻信號進行非線性壓縮處理從而達到壓低旁瓣和柵瓣的目的，同時保證了主瓣的展寬較小。通過分析發現，在時域合成算法中，由于算法的自身特點，當距離采樣起點存在誤差時也會引入柵瓣。

文獻[11]推導的時域合成算法包括4個主要步驟：時移、頻移、相位補償、相干疊加。其中，在時域進行頻譜搬移時，需要根據起始采樣時間和采樣頻率來構造線性相位因子。在實際雷達系統中，標定誤差會使實際起始采樣時間與標稱值存在誤差，該誤差會在寬帶合成信號中引入階梯相位，使寬帶合成信號脈沖壓縮后出現柵瓣。

本文首先簡要概述調頻步進頻的時域合成算法，建立了距離采樣起點的常數誤差模型，推導了該誤差與寬帶合成信號中階梯相位誤差的關系，從線性系統單位沖激響應的角度分析了距離起點誤差對柵瓣的包絡、高度、分布情況以及主瓣偏移的影響進行了定量分析，最后給出了仿真結果和實測數據結果。

2 信號模型和寬帶合成方法

調頻步進頻雷達通過脈內調頻，脈間頻率步進的方式擴展雷達帶寬，脈內調頻一般采用線性調頻方式。采用線性調頻步進頻體制的發射信號為

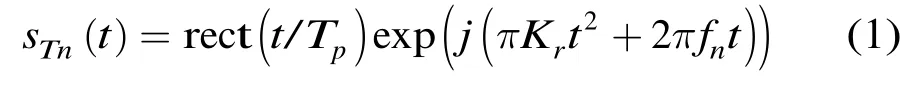
式(1)中，Kr為調頻斜率，Tp為脈沖寬度，子帶帶寬為B=KrTp,fn為子帶信號中心頻率。設步進頻雷達的載波中心頻率為fc，頻率步進點數為N，則fn可以表示為

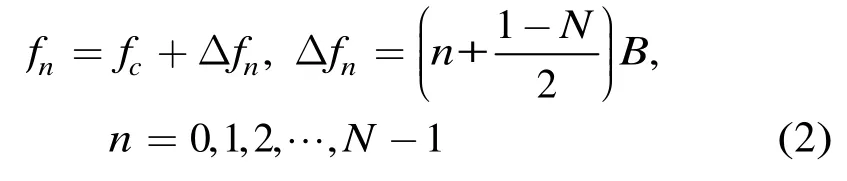
Δfn表示子帶中心頻率相對于寬帶信號中心頻率的偏移量。

調頻步進頻雷達一般采用高重頻信號，此時一個脈組周期“stop and go”假設仍然成立，即各子脈沖回波延時近似相同，設為τ，則解調后的基帶回波信號為

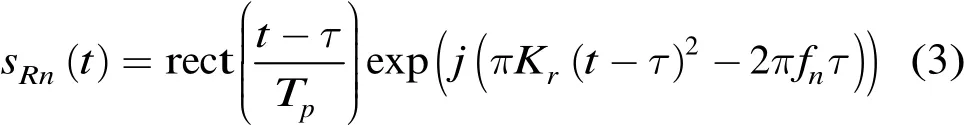
發射信號和解調后的基帶信號如圖1所示。

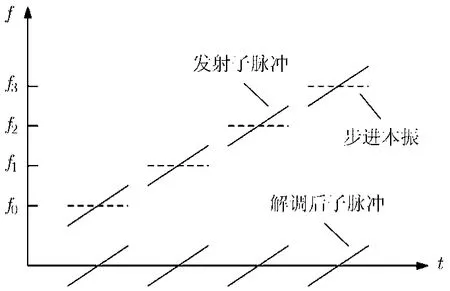
圖1 調頻步進信號

調頻步進頻雷達的回波信號首先進行帶寬合成處理，一般采用時域帶寬合成方法[12]。在時域帶寬合成算法的處理流程如圖2所示。

在調頻步進頻雷達系統中，子帶信號的采樣率通常小于寬帶信號的帶寬，因此在寬帶合成前需要進行升采樣，以保證進行頻移時各子帶信號的頻譜不會混疊。由于子脈沖的采樣窗長度通常小于寬帶信號脈寬，因此在寬帶合成前需要進行時域補零，以保證時移時子脈沖不會重疊。

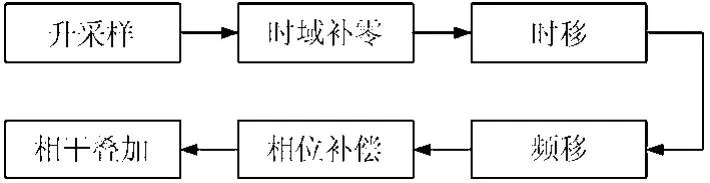
圖2 時域合成算法處理流程

3 距離起點誤差分析

3.1 誤差形式

在實際系統中，產生發射和采樣觸發信號的頻率源的實際值與標稱值會存在誤差，因此兩觸發信號的延時量，即實際起始采樣時間與設計值會存在誤差。由時間和距離的對應關系R=cτ/2，那么距離采樣起點的實際值與設計值會存在誤差。設距離起點設計值為Rideal，實際真值為Rmin，兩者之差即為距離起點誤差在時域合成算法中，頻移處理通常是將子帶信號在時域乘以線性相位因子exp(j2πΔfnt)完成，對于數字信號處理而言，需要構造時間軸。時間軸是利用起始采樣時間和采樣率來構造的。因此距離起點誤差會造成時域合成算法中時域補零后構造的時間軸與實際時間軸tax存在誤差，該時間誤差為Δtax=2ΔRax/c，即=tax+Δtax。那么頻移時與子帶信號相乘的線性相位因子變為exp(j2πΔfntax)exp(j2πΔfnΔtax)，即時間軸誤差會在各子帶信號中引入相位誤差2πΔfnΔtax，設為Δφn。由式(2)，Δfn為線性步進的，因此Δφn為階梯形的相位誤差。經過拼接處理后的寬帶信號x(t)與理想寬帶信號s(t)的頻譜關系為

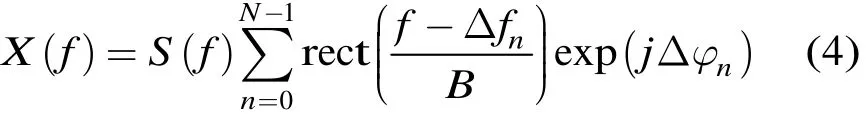
式(4)中的求和項即為距離起點誤差在寬帶拼接過程中引入的階梯相位誤差，設

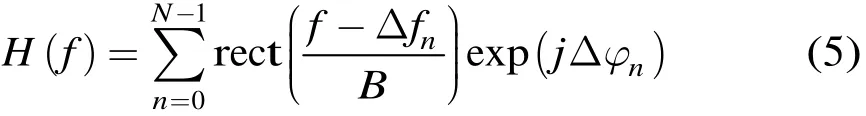
則X(f)=S(f)H(f)，即距離起點誤差引入的階梯相位對寬帶合成信號的影響等價于將理想寬帶信號通過頻率響應為H(f)的線性系統，該線性系統的單位沖激響應為

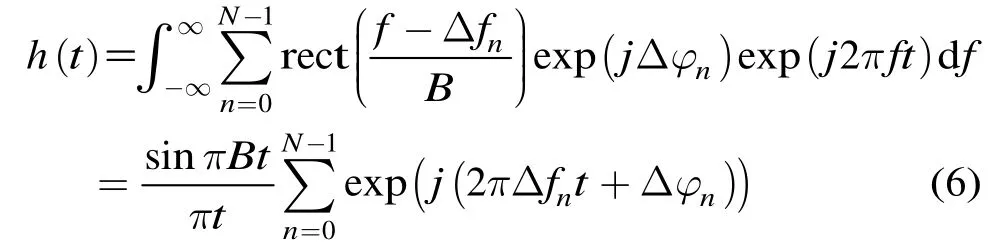
式(6)中各信號分量的初相為距離起點誤差引入的階梯相位，頻率為子帶信號中心頻率相對于寬帶信號中心頻率的偏移量。由式(2)中Δfn的定義可知，式(6)為一組諧波分量之和，包絡為sinc函數。對h(t)取模可得

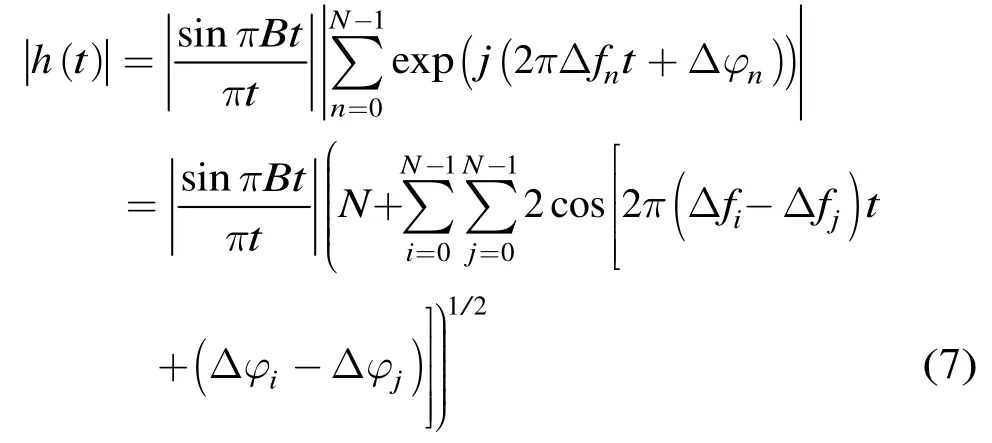
式(7)中余弦分量的頻率為Δfi-Δfj=(i-j)B，故復指數信號和式模的最小正周期為Tsum=1/B。由sinc包絡的零點位置為tzero=k/B,k為非零整數，即sinc包絡除去第1零點外，其余相鄰零點的距離為1/B。的形狀如圖3所示。

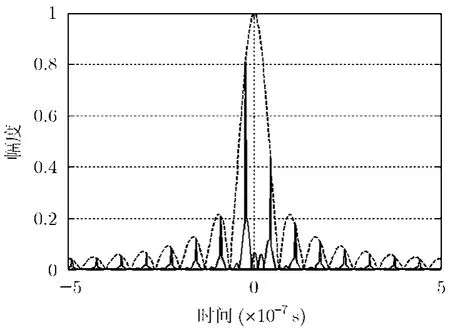
圖3 單位沖激響應幅度

從圖3中可以看到，單位沖激響應的模應存在很多周期性的尖峰，尖峰的包絡為sinc函數。由于尖峰的間隔與sinc包絡零點的間隔相等，因此當某一尖峰與sinc包絡的峰值點重合時，其余尖峰與sinc包絡的零點重合，此時單位沖激響應h(t)中只有一個尖峰。其余情況下單位沖激響應中會有周期重復的尖峰。

3.2 柵瓣產生

通過時域合成算法得到寬帶信號x(t)后需要進行脈沖壓縮處理。由卷積的性質可知，帶有相位誤差的寬帶合成信號脈沖壓縮后的結果，等價于理想寬帶信號的脈沖壓縮結果通過了單位沖激響應為式(6)的線性系統。由于該單位沖激響應包含了周期性的尖峰，因此脈沖壓縮結果會出現柵瓣，柵瓣間的距離為1/B，即子帶信號帶寬的倒數，主瓣和柵瓣具有sinc形狀的包絡。

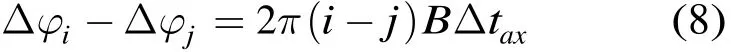
即初相為時間誤差Δtax的函數。當時間誤差變化時，周期性尖峰相對于sinc包絡移動，因此柵瓣的位置和高度隨Δtax變化。相位的周期為2π，各初相為2π整數倍的最小正周期為Tax=1/B，即柵瓣位置和高度隨時間誤差Δtax變化的周期為子帶帶寬的倒數。當時間誤差為該周期的一半，即1/2B時，周期性尖峰關于sinc包絡的峰值點對稱分布，此時寬帶合成信號脈沖壓縮后會出現兩個高度一樣的主峰，即第1柵瓣的高度和主瓣高度相同。

3.3 主瓣偏移

將階梯相位Δφn代入式(5)可得

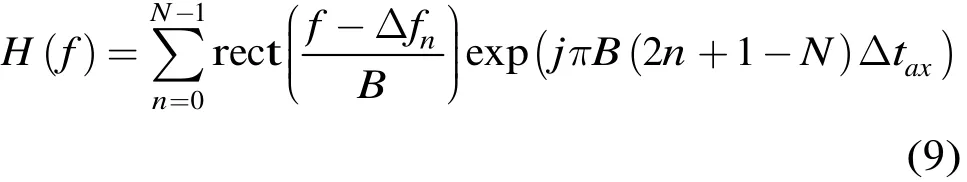
由于當步進點數N為奇數和偶數時，相位的分布情況不同。對當N為偶數的情況加常數相位偏移量，以便將兩種情況下的相位分布情況統一：

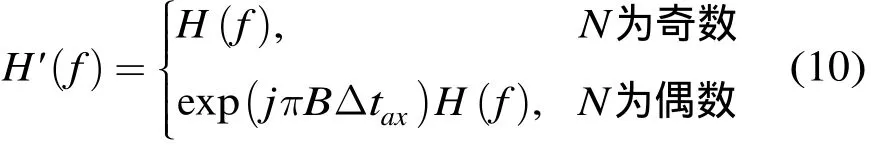
偏移處理后子帶信號相位中的最小正值均為Δφmin=2πBΔtax。設該相位對主值區間[-π,π)取模后的結果為即為Δtax對[-1/B,1/B)的主值區間取模的結果，并設模糊數為k。對其余相位做類似的去模糊處理，并保證相鄰相位的差在[-π,π)之間，則去模糊后的階梯相位變為該相位中包含的一階線性分量的斜率為

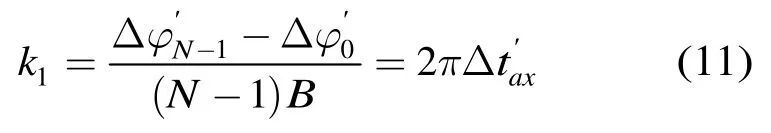
由傅里葉變換的性質，頻域的線性相位會導致時域信號的移位，即單位沖激響應h(t)中的主峰相對于sinc包絡的峰值點存在移位，偏移量為-，那么寬帶合成信號脈沖壓縮后的主瓣相對于sinc包絡峰值點的偏移量即為-。

設理想寬帶信號脈沖壓縮后主瓣位置為tm，則實際合成寬帶信號脈沖壓縮后主瓣位置為

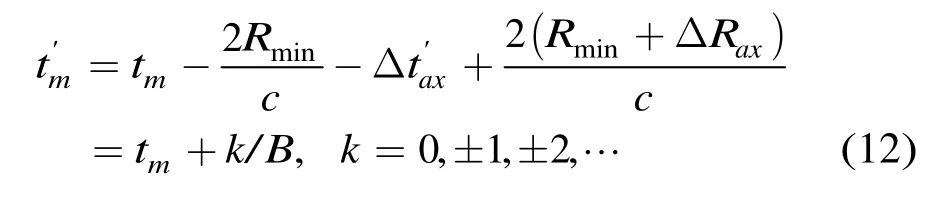
主瓣的位置的偏移會引入測距誤差，誤差大小為eR=kc/2B，即測距誤差恰為子帶信號分辨單元的整數倍。

3.4 柵瓣高度

由-π≤Δ＜π，則-1/2B≤＜-1/2B，柵瓣和主瓣的距離為1/B，則第1柵瓣相對于sinc包絡峰值點的偏移量為

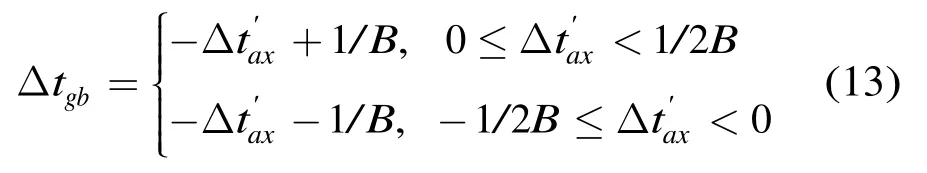
第1柵瓣與主瓣的相對高度為

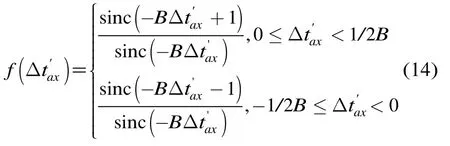
式中sinc函數的定義為sinc(θ)=sinπθ/πθ。化簡后為

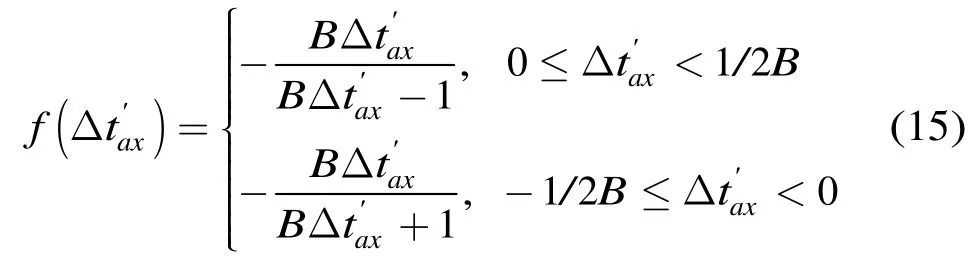
從圖4中可以看到，第1柵瓣高度隨著時間誤差絕對值的增大而增大，當時間誤差增大到±1/2B時，第1柵瓣高度和主瓣的高度相同，即出現兩個主峰。當子帶帶寬增大時，柵瓣高度對時間誤差更敏感，即相同的時間誤差會導致更高的柵瓣。

4 仿真結果

下面對調頻步進頻時域寬帶合成處理進行仿真，在各子脈沖中加入了常數距離起點誤差，從而觀察距離起點誤差對柵瓣分布和對主瓣偏移的影響。系統仿真參數如表1所示。

表1 仿真參數

4.1 柵瓣包絡和間隔

當引入時間誤差為Δtax=5/fs=13.9ns時，寬帶合成信號脈沖壓縮處理后的結果如圖5所示。

圖5中第1柵瓣高度為-11.48dB，已經高于第1副瓣。虛線為sinc函數，可以看到柵瓣的包絡確實為sinc形狀，從而驗證了式(6)的正確性。從圖中可以得出柵瓣間的間隔為66.39ns，而子帶帶寬的倒數為66.67ns，誤差小于一個采樣間隔2.78ns。因此驗證了柵瓣間隔為子帶帶寬的倒數這一結論的正確性。

當引入時間誤差為Δtax=1/2B=33.3ns時，寬帶合成信號脈沖壓縮后的結果如圖6所示。

從圖6中可以看到，柵瓣的包絡為sinc形狀。此時有兩個高度相同的主峰，即第1柵瓣的高度和主瓣相同，此時柵瓣性能最差，對成像結果的影響也最嚴重。因此，在實際系統中應避免時間誤差為(2k+1)/2B(k為整數)，對應的距離起點誤差為(2k+1)c/4B，即半個子帶信號分辨單元的奇數倍。

4.2 柵瓣高度和位置

下面改變時間誤差Δtax，觀察第1柵瓣高度、主瓣位置、柵瓣位置隨時間誤差的變化規律。其中，第1柵瓣隨時間誤差的變化情況如圖7所示。

從圖7可以看到，第1柵瓣的高度隨時間誤差Δtax是周期變化的，周期為66.67ns，即1/B。當時間誤差為k/B時(k為整數)，沒有柵瓣；當時間誤差為(2k+1)/2B時，柵瓣和主瓣高度相同。

主瓣位置和第1柵瓣位置隨時間誤差的變化情況如圖8所示。

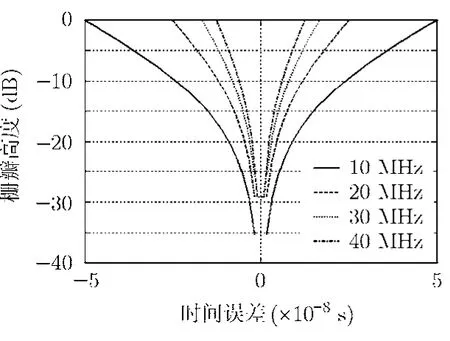
圖4 第1柵瓣高度隨時間誤差的變化

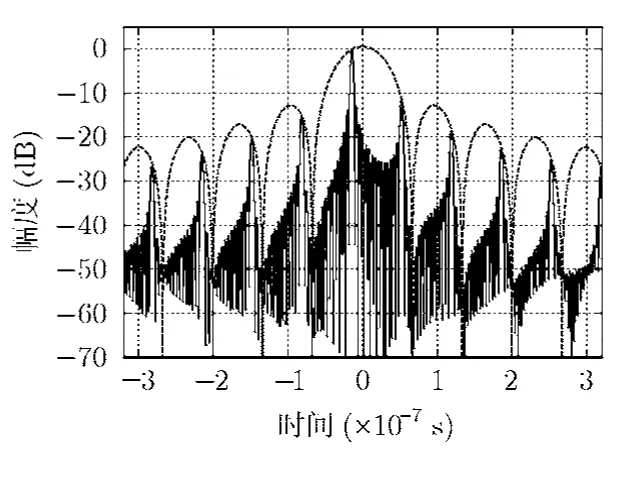
圖5 Δtax=1 3.9 ns 時的柵瓣分布

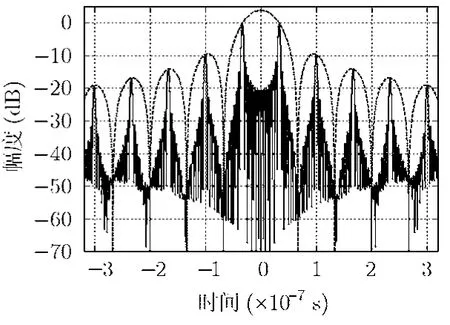
圖6 Δ t ax=3 3.3 ns 時的柵瓣分布

圖8中實線為主瓣位置，虛線為第1柵瓣位置。可以看到，主瓣位置隨時間誤差是單調增加的，時間誤差的絕對值越大，主瓣位置的偏移量越大，即測距誤差越大。主瓣位置曲線為階梯形，階梯的高度為1/B，因此主瓣的時間偏移量為k/B(k為整數)，對應的距離偏移量為kc/2B，這與前文的結論是吻合的。主瓣和柵瓣位置的距離始終為1/B，只是主瓣和柵瓣的相對位置有所變化，第1柵瓣交替出現在主瓣的左右側。這可以看成是隨著時間誤差的增加，第1柵瓣的高度也逐漸增加，當時間誤差為(2k+1)/2B時，第1柵瓣的高度與主瓣相同，當時間誤差再增加時，第1柵瓣的高度超過主瓣，從而柵瓣成為了主瓣，主瓣變為了柵瓣，主瓣和柵瓣的位置互換。

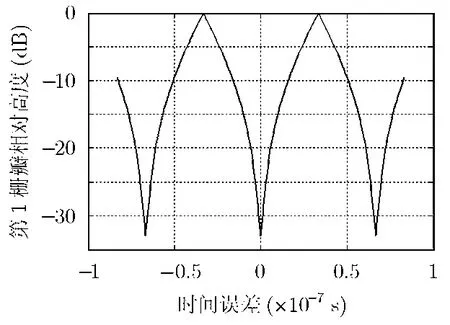
圖7 第1柵瓣高度

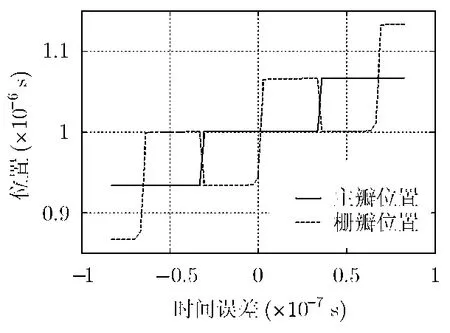
圖8 主瓣位置和柵瓣位置

5 實測數據結果

下面對一組實測數據進行寬帶合成和脈沖壓縮處理。實驗系統的參數如表2所示。

表2 實驗系統參數

寬帶合成信號的脈沖壓縮結果如圖9所示。圖中虛線為利用系統給定的距離起點參數進行寬帶合成和脈沖壓縮處理后的結果，可以看到寬帶合成信號的脈沖壓縮結果中存在明顯的柵瓣，柵瓣間隔為子帶帶寬的倒數。第1柵瓣的高度為-2.62dB，這會在最終的成像結果中引入大量的虛假目標，嚴重影響成像質量。

由于柵瓣的出現是由距離起點誤差導致的，因此可以通過修正距離起點來減小距離起點誤差導致的階梯相位，從而降低柵瓣，減小誤差的影響。通過迭代修正值，可以獲得柵瓣最低的1維像，如圖9中的實線所示，在修正后的脈沖壓縮結果中，幾乎看不到柵瓣。時間修正量為36.67 ns，大于1/2B，因此會導致主瓣位置的偏移，時間偏移量為1/B，對應的距離偏移量為10 m。比較圖中距離起點修正前后的主瓣位置，修正前的主瓣位置為2478.8 m，修正后的主瓣位置為2488.8 m，主瓣偏移量為10 m，與理論推導相吻合。因此，實測數據驗證了主瓣偏移結論的正確性。對比實測數據指出：距離起點修正前后的脈沖壓縮結果說明通過對距離起點的修正可以極大地壓低柵瓣，從而使柵瓣水平滿足成像要求。

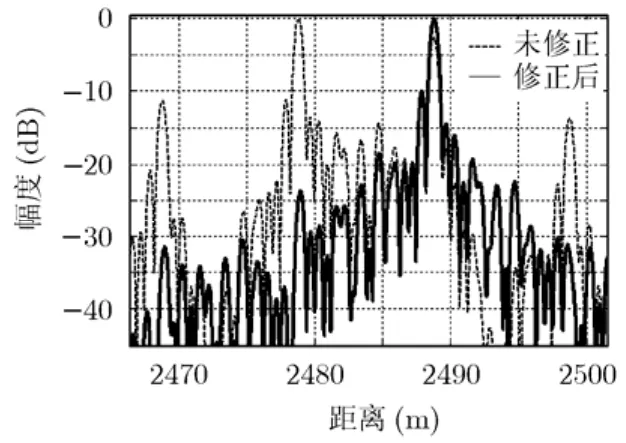
圖9 實測數據處理結果

6 結論

距離起點誤差會在寬帶合成信號中引入階梯相位，從而導致脈沖壓縮結果中出現柵瓣。通過分析發現，柵瓣是周期重復的，周期為子帶帶寬的倒數，柵瓣的包絡為sinc形狀。若發射的子帶信號在頻率上有重疊，則柵瓣重復周期為回波信號濾波后子帶帶寬的倒數，即頻率步進值的倒數。通過分析，得到了第1柵瓣與主瓣的相對位置和相對高度。除了引入柵瓣，距離起點誤差還會造成主瓣位置的偏移，導致測距誤差，測距誤差隨距離起點誤差單調增加，呈階梯形變化。最后，通過仿真和實測數據的處理，驗證了以上結論的正確性。

[1]Ender J H G and Brenner A R.PAMIR - a wideband phased array SAR/MTI system.IEE Proc.Radar,Sonar and Navigation,2003,150(3): 165-172.

[2]Cerutti-Maori D,Klare J,Burger W,et al..Wide area traffic monitoring with the PAMIR system.Geoscience and Remote Sensing Symposim,IGARSS 2007,Barcelona,2007:3567-3570.

[3]Nie Xin,Zhu Dai-yin,Mao Xin-hua,et al..The application of the principle of Chirp scaling in processing stepped Chirps in spotlight SAR.IEEE Geoscience and Remote Sensing Letters,2009,6(4): 860-864.

[4]Luo Ying,Zhang Qun,and Qiu Cheng-wei.Micro-Doppler effect analysis and feature extraction in ISAR imaging with stepped-frequency Chirp signals.IEEE Transactions on Geoscience and Remote Sensing,2010,48(4): 2087-2098.

[5]Zhu Feng and Zhang Qun.Reconstruction of moving target’s HRRP using sparse frequency-stepped Chirp signal.IEEE Sensors Journal,2011,11(10): 2327-2333.

[6]Deng Yun-kai,Zheng Hui-fang,and Wang R.Internal calibration for stepped-frequency Chirp SAR imaging.IEEE Geoscience and Remote Sensing Letters,2011,8(6):1105-1109.

[7]Levanon N and Monzeson E.Nullifying ACF grating lobes in stepped-frequency train of LFM pulses.IEEE Transactions on Aerospace and Electronic Systems,2003,39(2): 694-703.

[8]Gladkova I and Chebanov D.Grating lobes suppression in stepped-frequency pulse train.IEEE Transactions on Aerospace and Electronic Systems,2008,44(4): 1265-1274.

[9]Gladkova I.Analysis of stepped-frequency pulse train design.IEEE Transactions on Aerospace and Electronic Systems,2009,45(4): 1251-1269.

[10]李海濱,張云華.降低調頻步進信號副瓣的方法研究.現代雷達,2006,28(4): 45-49.

[11]Lord R T and Inggs M R.High resolution SAR processing using stepped-frequencies.Proc.IEEE Geoscience Remote Sensing Symposim,IGARSS 1997,Singapore.August 1,1997:490-492.

[12]李海英.超寬帶信號波形及其合成孔徑雷達成像研究.[博士論文],中國科學院電子學研究所,2002.