結晶器非正弦振動工藝參數優化

孫德建，王 博，汪程鵬

(西北工業大學材料科學與工程學院，陜西 西安710072)

結晶器非正弦振動工藝參數優化

孫德建，王 博，汪程鵬

(西北工業大學材料科學與工程學院，陜西 西安710072)

在正弦振動波形的基礎上，利用分段函數法構造出一種非正弦振動波形，導出振動的6個工藝參數，建立了工藝參數優化的數學物理模型，給出了設計變量、約束條件、目標函數。先進行了單目標函數的優化，分別求出了6個分目標函數在約束條件下的變化范圍，再利用轉化指標法對6個分目標函數進行加權整合，給出多目標函數的表達式并進行求解。

非正弦振動波形;工藝參數;目標函數;參數優化

0 前言

在結晶器振動過程中，與鑄坯直接接觸的只有結晶器與保護渣，要想改善鑄坯質量，可從這兩個方面入手，即開發高速連鑄用保護渣或有利于潤滑的結晶器振動模型。作為一種具有極大優越性的振動模型，非正弦振動不僅可實現振幅和正、負滑脫比例的在線調整，還有利于保護渣向結晶器壁和鑄坯之間縫隙均勻滲透，可顯著改善結晶器內壁的潤滑效果，減輕鑄坯表面振痕深度，減少拉裂、拉漏并提高鑄坯表面質量，為連鑄生產提供保證［1-2］。本文在正弦振動波形的基礎上引入了一種非正弦振動波形。在結晶器振動過程中，有6個工藝參數最終影響了鑄坯質量［3］，而目前關于結晶器工藝參數優化問題，絕大多數的文獻集中在論述保證一個或少數幾個工藝參數取值最佳情況下振動參數應取數值，本文建立了振動波形工藝參數優化模型，并結合相關文獻數據［4-6］進行了求解，目前此種優化模型和方法未見報道。

1 非正弦振動波形

在正弦振動曲線的基礎上，利用分段函數法構造出一種非正弦振動波形，其振動位移和速度曲線如圖1所示。該非正弦振動波形的振動位移和速度表達式分別為式(1)和式(2)。

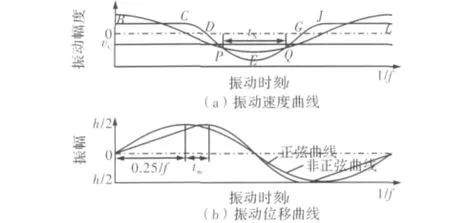
圖1 振動速度和位移曲線Fig.1 Curves of non-sinusoidal oscillation speed and displacement

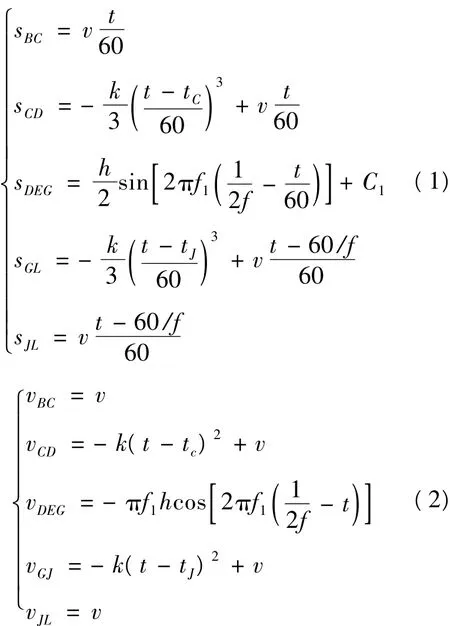
余弦曲線段DEG的頻率為f1=f/(1－α)

拋物線CD段頻率為

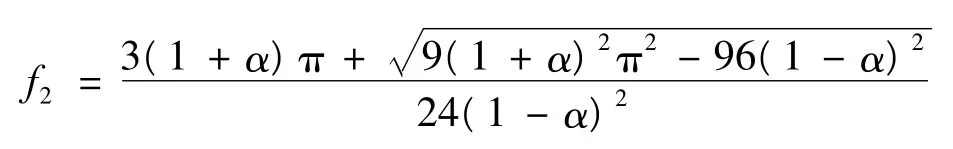
一個振動周期內，tC、tD、tG、tL分別為

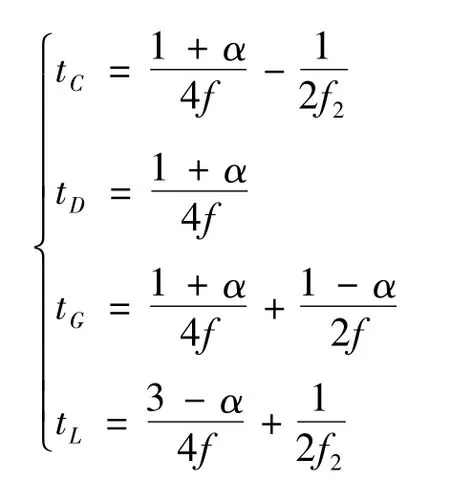
反映最佳振動模式特點的工藝參數有負滑動時間tN、正滑動時間tP、負滑動超前量NSA和負滑動率NS、負滑動時間比率NSR、最大滑脫相對速度差Δv等。這六個振動工藝參數的表達式分別為

2 工藝參數優化數學模型的建立及求解

2.1 模型的建立

觀察工藝參數表達式可看出，共有4個獨立變量影響工藝參數取值，它們分別為振頻f、振幅h/2、非正弦波形偏斜率α、拉坯速度vc。以這四個獨立變量為設計變量，以實際生產中工藝參數應滿足的范圍為約束條件，可對工藝參數進行優化，進而保證鑄坯質量。

非正弦波形偏斜率α對所有工藝參數的影響都有益，而且取值越大越有利。但取值過大，使得結晶器向下振動的加速度會變得很大，進而造成對設備的沖擊和工作的不平穩。根據經驗，一般α應取0～0.4。因此優化設計變量為

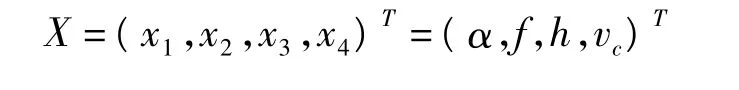
為確保鑄坯的質量和順利脫模，各工藝參數在實際生產中應滿足一定范圍，超出此范圍，鑄坯的質量會受到不同程度的影響。因此選取振動工藝參數表達式分別與在保證鑄坯質量情況下工藝參數應滿足范圍的上限和下限的差的絕對值的乘積的相反數為目標函數，其取值越小，工藝參數取值最佳。針對負滑動時間tN、正滑動時間tP、負滑動超前量NSA和負滑動率NS、負滑動時間比率NSR、最大滑脫相對速度差Δv，有以下各式:

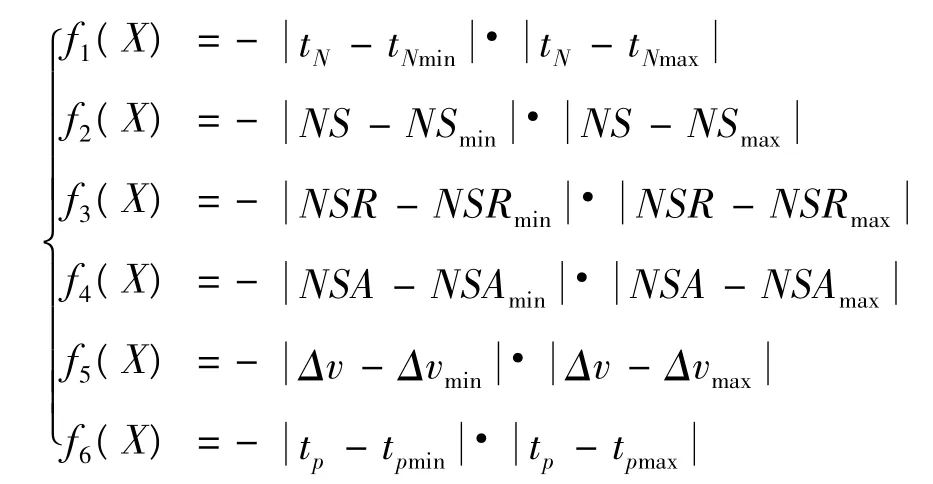
上面各式中的下標分別表示為保證鑄坯質量，該工藝參數應滿足范圍的上下限。在實際生產過程中，為確保鑄坯質量，必須把工藝參數約束在一定的范圍內，即

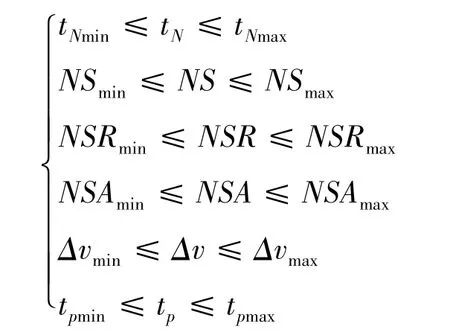
上面各式中，tN，NS，NSR，NSA，Δv，tP分別對應分目標函數f1(X)～f6(X)。為確保負滑動時間在0.1 s附近，通過圖2可看出，Z值較大時，負滑動時間曲線幾乎垂直上升，頻率的微小變化能引起tN的很大變化，因此Z的取值不宜過大。而當Z值較小時，臨界頻率f0(tN曲線與f軸的交點)較高，因此在實際應用中Z值的取值也不宜過小，3≤Z=h/vc≤7。

2.2 單目標函數的優化

可以看出，這是一個多目標函數的優化問題，共有6個目標函數，4個設計變量，還有8個不等式約束。由于6個工藝參數的重要程度不同，且各目標函數在數量級上難于達到統一平衡，因此選取多目標函數優化方法中的轉化設計指標法建立優化模型進行求解。本文根據有關文獻，以下列適宜工藝參數取值(對應于能保證鑄坯質量時工藝參數取值的極限)為例進行求解，具體數據見表1。以此數據為例，我們研究在約束條件下每個單目標的優化情況。

分別將f1(X)～f6(X)作為目標函數，將上面的約束條件作為約束函數，編制matlab程序進行求解。在matlab優化工具箱optimization Tool下，選擇好求解器，算法，objfun1.m，confun.m，初始點之后，在右邊的繪圖工具中選擇Function Value選項等等，這樣就可繪出單目標函數的優化迭代過程。其中需要注意的是，若要求解目標函數的最大值，可通過將目標函數整體表達式乘以－1的方式間接求出。圖3是單目標函數f1(X)最小值和最大值的優化迭代過程(f2(X)～f6(X)優化迭代過程省略)。

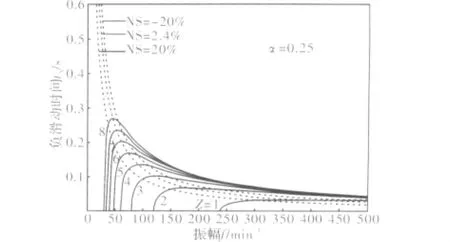
圖2 α=0.25時第一種非正弦振動的tN和NS曲線Fig.2 The tN and NS curves of non-sinusoidal vibration whileα=0.25

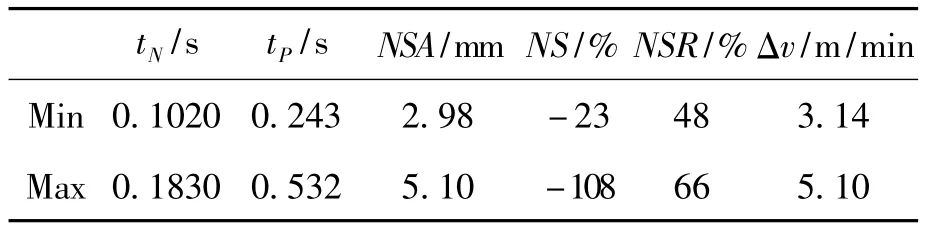
表1 非正弦振動工藝參數的變動范圍Tab.1 Variation range of non-sinusoidal oscillation parameters

由圖3可看出各分目標函數(或設計指標)在約束條件下的變動范圍(最小值和最大值之間)，見表2。

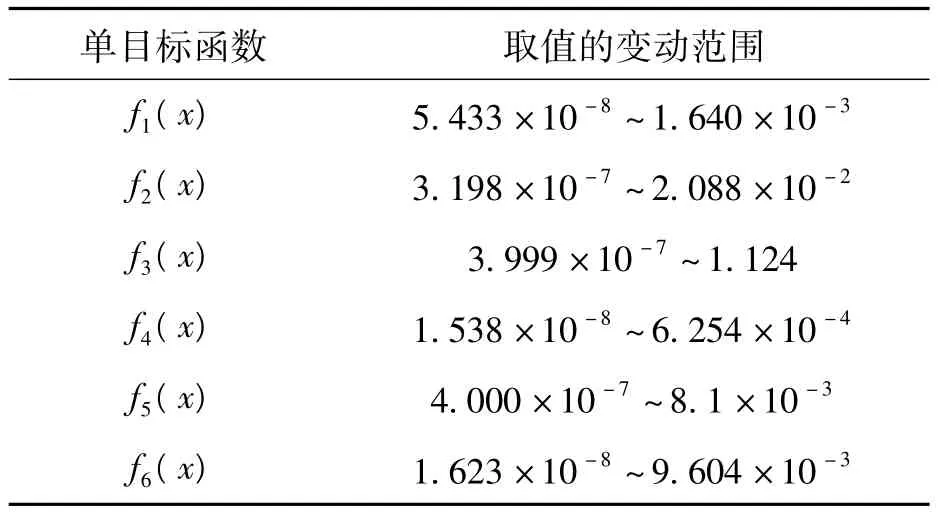
表2 單目標函數取值的變動范圍Tab.2 Value range of single objective functions

2.3 多目標函數的優化

由于6個單目標函數在數量級上難于達到統一平衡，選取轉化指標法［7］進行求解優化。利用正弦函數y=(x－sin x)/(2π)(0≤x≤2π)對上面的6個單目標函數進行轉換，使其規格化。

如已知f1(x)的變動范圍為5.433×10－8～1.640×10－3，則對應于f1(x)值轉換函數的自變量為，單目標函數f1(x)轉換后變為fT1(x)，且，對其余5個單目標函數采用相同操作得fT2(x)，fT3(x)，fT4(x)，fT5(x)，fT6(x)，最后，“統一目標函數”為，加權因子ωj(j=1，2，…，q)根據該項設計指標在最優化設計中所占重要程度確定。

圖3 單目標函數f1(X)最小值和最大值的優化迭代過程Fig.3 Optimization iterative process ofminimum and maximum values of objective function f1(x)

選取 ω1=0.5，ω2=0.1，ω3=0.1，ω4=0.15，ω5=0.05，ω6=0.1，在matlab建立多目標函數的objfun.m文件，并以單目標約束函數confun.m作為多目標約束函數，選擇fmincon求解器，內點法算法，完成在matlab優化工具箱里優化問題的建立，求解之后可看出，該優化過程進行了102次迭代，最終收斂，并得到優化點［0.063，116.36，8.861，1.376］。圖4為多目標函數的迭代優化過程。

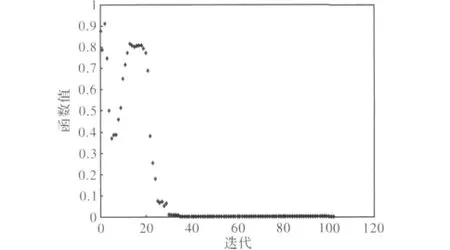
圖4 多目標函數f(X)的優化迭代過程Fig.4 Optimization iterative process ofmulti-objective function f(X)

需要注意的是，在實際生產中，若要保持四個變量中的一個或幾個不變，可通過設置變量滿足的范圍加以實現，即讓該變量的上限等于下限。根據實際設備情況，將設備調整到接近最優解的振幅、振頻、拉速、非正弦波形偏斜率。

4 結論

(1)為改善鑄坯質量和減輕振痕深度，可引入一種非正弦振動波形，推導出表征該振動波形的6個工藝參數是振動基本參數α、f、h和拉坯速度vc的函數，這為建立優化數學物理模型提供了基礎。

(2)為保證鑄坯質量，各工藝參數應在適宜的范圍內變動，在此范圍已知的情況下，可利用優化模型進行求解。通過對模型進行優化，可取得工藝參數取值最佳情況下振動基本參數和拉速所取數值，這一優化過程為鑄坯質量的提升創造了條件。

［1］EDWARD S．Overview ofmold oscillation in continuous casting［J］．Iron and Steel Engineer，1996，73(7):29-37．

［2］MIKIO S，HIDEAKIM，TOM K，et a1．Development of a new mold oscillationmode for high-speed continuous casting of steel slabs［J］．ISIJ International，199131(3):254-261．

［3］李憲奎，張德明．連鑄結晶器振動技術［M］．北京:冶金工業出版社，2000．

［4］孟祥寧，朱苗勇．連鑄結晶器非正弦振動波形構造及參數研究［J］．中國機械工程，2007，18(15):1779．

［5］任廷志．結晶器非正弦振動參數的構建及取值限度［J］．重型機械，2004(2):38-54．

［6］洪秋華，胡大超．基于傅立葉級數的非正弦振動波形的研究［J］．重型機械，2008(3):15-19．

［7］劉惟信．機械最優化設計(第二版)［M］．北京:北京大學出版社，1994，230-234．

Optim ization for technological parameters of crystallizer non-sinusoidal vibration

SUN De-jian，WANG Bo，WANG Cheng-peng
(School of Materials Science and Engineering，Northwestern Polytechnical University，Xi'an 710072，China)

Based on sinusoidal oscillation waveform，a non-sinusoidal oscillation waveform was structured with the paragraph-function method，its 6 technological parameters were derived，amathematical physicsmodel for optimizing the technical parameters was established．The design variables，constraint conditions and objective function are given in this paper．The single objective functionswere optimized first．The variation range of the 6 single objective functions under the constraint conditons is found out，and then the 6 single objective functions are integrated intomuti-objective function by using transformation index method．Finally，the expression of a muti-objective function is presented and solved．

non-sinusoidal oscillation waveform;technological parameter;objective function;parameter optimization

TF777.1

A

1001－196X(2012)04－0042－05

2012－03－01;

2012－04－10

孫德建(1985－)，男，西北工業大學材料科學與工程學院博士生，主要從事定向凝固高溫合金及連鑄結晶器振動技術的相關研究。