基于MM-EMD的改進HHT及應用

梁 升，王新晴，王 東，夏 天，錢淑華

(1.解放軍理工大學，南京 210007;2.海軍工程研究設計局，北京 100841)

1 Hilbert-Huang變換的局限性

與小波等方法相比，雖然Hilbert-Huang變換(Hilbert-Huang Transform，HHT)是一種非先驗的方法，但仍然假定信號由本征模態分量(Intrinsic Mode Function，IMF)和普通趨勢項構成[1]。IMF滿足兩個條件:① 整個信號長度上極值點和過零點的數目必須相等或只差一個;② 在任意時刻，由極大值定義的上包絡線和由極小值定義的下包絡線的平均值為0。這兩個條件實際上表示了一種波動的模式。如果被分析的信號僅僅由多個IMF分量與普通趨勢項組成，那么，經驗模態分解(Empirical Mode Decomposition，EMD)所得到的IMF分量大都具備明確的物理意義，HHT能取得較好的分析效果。而工程實際中，信號是由多種分量組合而成的，不是單純的IMF分量與普通趨勢項的結合，因而當信號中存在非普通趨勢、非IMF分量時HHT分析的效果并不理想。圖1所示方波信號是一種典型的、可能具有特定的物理意義的非趨勢、非IMF分量。

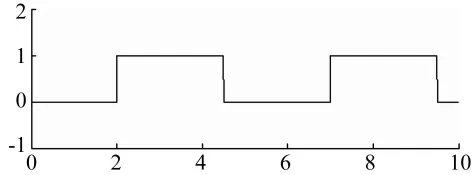
圖1 方波信號Fig.1 Square wave signal

2 廣義趨勢項

針對HHT方法存在的上述局限，提出改進思路:當原始信號中可能存在非IMF分量時，先將非IMF分量分離出來，再對剩余信號進行HHT分析。

EMD分解得到的趨勢項一般為常數或單調函數。而工程實際中，系統在受到強大外力作用或內部結構發生巨大變化的情況下，相關的信號幅值或其他特征會發生急劇變化，從而使信號趨勢產生漸變甚至突變，當外力作用或系統內部結構變化具有周期性時，相應的信號趨勢也可能具有周期性。本文將信號中反映這種趨勢的分量稱為廣義趨勢項。廣義趨勢項與傳統意義上的趨勢項不同。在早期對時間序列的研究中，趨勢項一直被看作時間序列長時間的動向，但是迄今為止，趨勢項在數學上并沒有一個準確的定義，一般認為，趨勢項是測試信號中周期遠大于信號記錄時間長度的成分[3]。而廣義趨勢項主要反映了待測系統在外力、內力的綜合作用下相應信號的主要變化動向，它既包括了傳統意義上的趨勢(長期趨勢)，也包括了部分短期趨勢。廣義趨勢項不一定是IMF分量。

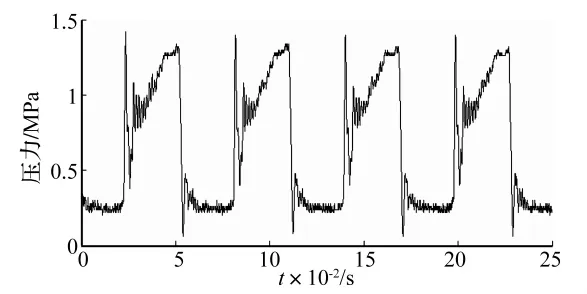
圖2 實測夾緊缸工作過程中夾緊腔油壓波動波形Fig.2 The oil pressure fluctuation signal under the periodic excitation

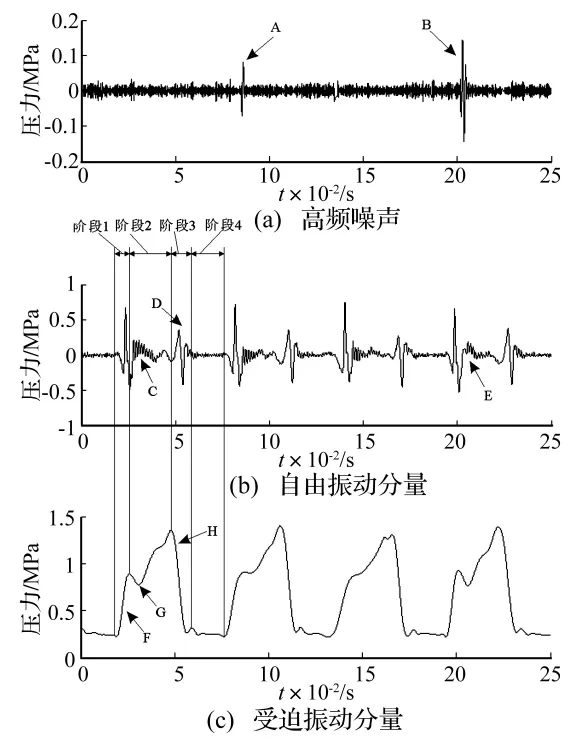
圖3 原信號基于EMD分解重組后得到的三個分量Fig.3 The three components of the pressure signal based on EMD

與一般的機械振動加速度信號、地震加速度信號不同，液壓系統內部的壓力信號不是以零軸為中心的上下波動，而是隨著系統狀態、外部負載等因素的改變而逐漸變化，如果出現波動，也是以一定趨勢為中心的上下波動。油壓信號的廣義趨勢項就是由這些不同時段的相應趨勢所構成的，它由系統狀態、外部負載等因素決定，一般情況下不滿足IMF分量的條件。以周期激勵下的夾緊缸內油壓波動信號(圖2)為例，文獻[2]運用傳統HHT方法將其分解為受迫振動、自由振動的組合(圖3)，其受迫振動分量就是該信號的廣義趨勢項，而自由振動分量可以看作是以相應時刻受迫振動分量為中心的上下波動。以上自由振動與受迫振動分量都是通過EMD分解重組得到的。由前文知，EMD對于本身帶有非IMF分量的信號，其分析效果會受到“IMF假設”的影響，如果先用某種方法分離出原始信號中不屬于IMF分量的廣義趨勢項，再對剩余信號進行HHT分析，可能得到更好的分析效果。

3 基于MM-EMD的HHT改進算法

前人主要在以下兩個方面對數學形態學(Mathematical Morphology，MM)與HHT的結合進行了研究:用數學形態濾波器對信號進行濾波降噪預處理，然后再進行HHT分析[4－5];先對信號進行 EMD 分解，再對篩選出的IMF分量進行基于數學形態濾波器的降噪處理[6]。

MM－EMD不同于以上方法，其基本思想是運用數學形態濾波器提取出不利于EMD分解的廣義趨勢項等低頻非IMF分量，再對剩余信號分量進行EMD分解。具體步驟如下:

(1)對原信號 x(t)={x1，x2，…，xN}進行傅里葉變換，估計出自由振動信號最大頻率fq。

(2)運用開－閉和閉－開組合形態濾波器處理信號[7－8]，分離出廣義趨勢項 Xq(t)及余項 Xr(t)。數學形態濾波器的結構元素選用方形結構元素。根據fq與原信號的采樣頻率fs確定方形結構元素長度M=fsfq，當廣義趨勢項并不明顯時，可令M=N/4。根據原信號x(t)自身特點，可以選取原始信號相鄰數據之間差額絕對值中的非零最小值K作為結構元素的高度，即且 K≠0。

(3)對余項Xr(t)進行經驗模態分解，得到若干IMF分量和一殘量rn;

(4)運用相關系數法、互信息、頻域特征等方法對IMF分量進行篩選，對篩選出來的IMF分量進行Hilbert譜分析。

需要說明四點:① 大量仿真與實測信號處理結果表明，與三角形、半圓形結構元素相比，方形結構元素提取信號突變特征特別是突變趨勢的效果較好，因而以上過程選用方形結構元素;② 噪聲與突變引起的信號相鄰數據差值的絕對值遠大于信號按自身規律變化時相鄰數據差值的絕對值，原始信號相鄰數據之間差值絕對值中的非零最小值K接近于信號按自身規律變化時相鄰數據的最小差值，大量仿真試驗表明，當平結構元素的高度選擇為K時，可以有效提取出包含準確突變信息的趨勢項，同時濾除一定程度的噪聲特別是脈沖噪聲;③ 自由振動信號最大頻率fq可以根據實際情況進行修正;④ 如果其他方法也可以有效分離出廣義趨勢項，即可將以上步驟中的(1)、(2)改為采用其他方法，步驟(3)、步驟(4)不變。

4 實例

分別用傳統HHT方法與基于MM－EMD的改進HHT方法對仿真信號與實測信號進行處理，檢驗新方法的分析效果。

4.1 仿真信號

仿真信號由頻率為4 Hz的方波信號與間斷產生的頻率為50 Hz的正弦信號疊加而成，如圖4所示，采樣頻率fs=2 000 Hz，采樣點數N=2 000。對該信號進行EMD處理后得到六個IMF分量和一個殘量。分別對各個分量進行Hilbert譜分析，最終得到與原始信號自相關系數最高的 c1分量的 Hilbert-Huang譜，如圖5所示。

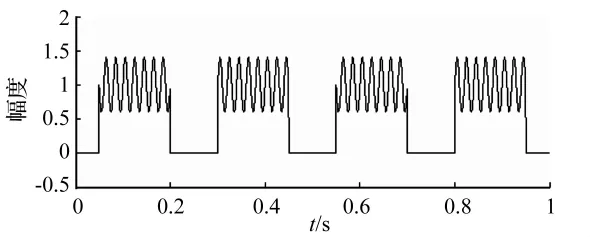
圖4 仿真信號時域圖Fig.4 Simulated signal

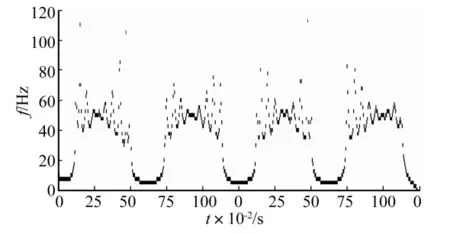
圖5 仿真信號的傳統HHT方法分析結果Fig.5 The analysis result of the simulated signal based on traditional HHT

原始信號中最高頻率成分為50 Hz，因而取fq=50 Hz。方形結構元素長度M=fs/fq=40。根據原始信號可以計算出方形結構元素高度采用由此形態結構元素構成的開－閉和閉－開組合形態濾波器對原始信號進行形態濾波處理，得到廣義趨勢項Xq(t)與余項Xr(t)，如圖6(a)，圖6(b)所示。

圖6 仿真信號的數學形態濾波結果Fig.6 The filtered result of simulated signal based on MM

對余項Xr(t)進行EMD處理，得到六個IMF分量和一個殘量。分別對各個分量進行Hilbert譜分析，最終得到余項Xr(t)中與原始信號自相關系數最高的c1分量的Hilbert-Huang譜，如圖7所示。

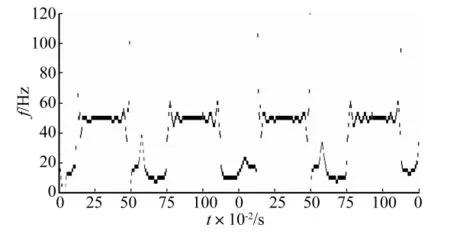
圖7 仿真信號基于MM－EMD的改進HHT分析結果Fig.7 The analysis result of the simulated signal based on improved HHT by MM-EMD

對比圖5與圖7，可以明顯看出經過MM-EMD方法改進后的Hilbert-Huang譜更能清晰準確地反映50 Hz信號分量出現的時間－該分量的時頻分布主要集中于50 Hz附近且較少發散。仿真信號處理結果一方面表明，傳統HHT方法在處理含非IMF分量的信號時存在局限－信號中的非IMF分量會降低HHT分析效果，另一方面展示了基于MM-EMD的改進HHT方法的有效性。

4.2 實測信號

運用基于MM－EMD的改進HHT方法來分析實測油壓信號，一方面檢驗新方法的效果，另一方面將新方法應用于油壓信號分析，以提取、識別油壓信號中蘊含的液壓系統動態特性。

該信號的時域圖如圖2所示。文獻[2]指出，周期激勵下的夾緊缸油壓信號由受迫振動、自由振動、噪聲等三種分量組成，并通過EMD分解、重組得到了該信號的三個分量(圖3)。本節運用基于MM-EMD的改進HHT方法對該信號進行再分析。具體步驟如下:

(1)信號采樣頻率fs=1 000 Hz。根據文獻[2]中模型計算出的自由振動頻率估計值(224 Hz)，取fq=400 Hz。方形結構元素長度M=fs/fq=25。

(3)對余項Xr(t)進行EMD處理，得到12個IMF分量和一個殘量。

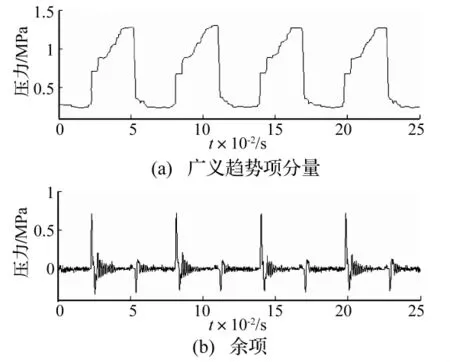
圖8 液壓缸油壓信號的數學形態濾波結果Fig.8 The filtered result of pressure signal based on MM

(4)運用文獻[2]中介紹的方法，根據各IMF分量的頻率分布情況，將各IMF分量分類:c1主要為高頻噪聲;自由振動分量主要集中于 c2，c3，c4，c5，c6，c7 等頻率分布在100～500 Hz的分量;其余分量則包含了受迫振動分量。在此基礎上對信號進行重構:自由振動分量由 c2，c3，c4，c5，c6，c7 等分量疊加而成，而受迫振動分量由 c8，c9，c10，c11，c12、r等分量與廣義趨勢項Xq(t)疊加而成。重組可得最終結果，如圖9所示。

與文獻[2]中傳統HHT方法相比，基于MM-EMD的改進HHT方法可以得到更好的分析效果:

(1)新方法在一定程度上抑制了模態混疊現象。對比圖3(a)和圖9(a)可以發現，由于模態混疊，傳統EMD方法得到的高頻噪聲分量中出現了0.08 s左右幅度大于0.12 MPa的波動、0.2 s左右幅度大于 0.2 MPa的波動(圖3(a)A、B處)，基于MM-EMD的方法得到的高頻噪聲分量雖然也具有一定的模態混疊現象，但波動幅度都不大于0.1 MPa。

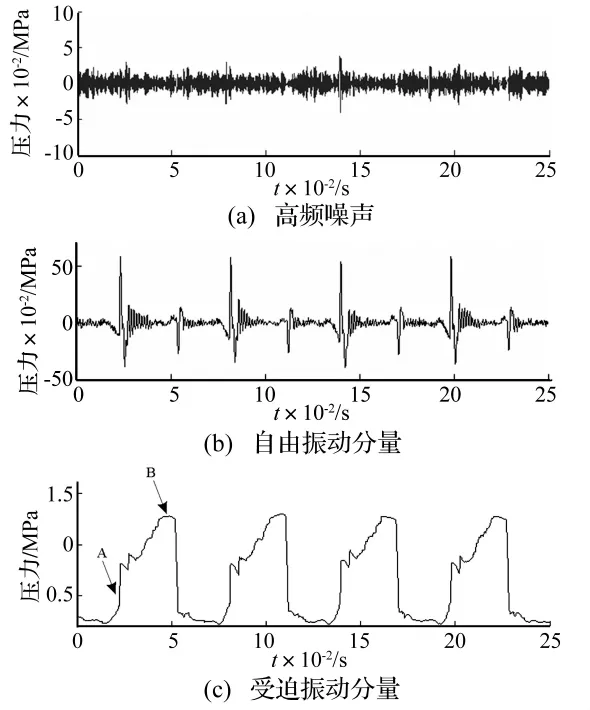
圖9 夾緊缸壓力信號基于MM-EMD分解重組結果Fig.9 The three components of the pressure signal based on MM-EMD

(2)新方法得到的自由振動分量與受迫振動分量體現的物理意義更為明顯。圖9(b)中油壓基本上是以0軸為中心上下波動，而圖3(b)中部分時間段(圖3(b)C、E處)的油壓在0軸以上波動。受迫振動分量與凸輪撞擊液壓缸的過程更為吻合:凸輪撞擊瞬間，油壓迅速上升，圖9(c)中A處上升段的斜率大于圖3(c)中F處的斜率，油壓上升后一段時間內在1.3 MPa保持平穩，圖3(c)沒有這一階段(圖3(c)中H處)，而圖9(c)中B處較好地反映了這一過程。傳統HHT方法得到的受迫振動的壓力上升沿與下降沿的斜率小于原始信號(圖2)的原因可能是:傳統HHT方法把屬于趨勢項(受迫振動)的信號分量錯誤地分解到自由振動分量中。

以上兩點表明，與傳統HHT方法相比，基于MMEMD的改進HHT方法得到的自由振動分量所反映的壓力波動信息更為真實可信，在處理油壓信號時，新方法的分析效果更好。

5 結論

與傳統HHT方法相比，基于MM-EMD的HHT改進方法增加了基于形態學的廣義趨勢項提取過程，雖然在一定程度上增加了信號處理的計算量，但由于形態變換的實現算法只包含布爾運算、加減法運算而不需要做乘法，因而提取過程消耗的時間較少。在相同的硬件條件下運用兩種方法處理文中仿真信號時，傳統方法消耗時間為3.35 s，而新方法消耗時間為4.39 s，其中廣義趨勢項提取過程只消耗了0.39 s，趨勢項提取后的EMD與Hilbert譜分析消耗了4.00 s。雖然新方法在一定程度上增加了計算時間，但仿真與實測油壓信號的處理結果表明，對于部分含有非IMF分量、非普通趨勢項成分的信號，新方法能取得比傳統HHT方法更好的分析效果。

[1]Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proc.Roy.Soc.Lond，1998，454:903 －995.

[2]王新晴，梁 升，夏 天，等.基于HHT的液壓缸動態特性分析新方法[J].振動與沖擊，2011，30(7):82 －86，159.WANG Xin-qing，LIANG Sheng，XIA Tian，et al.A new method based on HHT for analyzing dynamic characteristics of a hydraulic cylinder[J].Journal of Vibration and Shock，2011，30(7):82 －86，159.

[3]Bendat J S， Piersol A G. Random data:analysis and measurement procedures[M].New York:John Wiley and Sons，1986.396－398.

[4]胡愛軍.Hilbert-Huang變換在旋轉機械振動信號分析中的應用研究[D].保定:華北電力大學，2008.

[5]胡愛軍，唐貴基，安連鎖.基于數學形態學的旋轉機械振動信號降噪方法[J].機械工程學報，2006，42(4):127－130.HU Ai-jun，TANG Gui-ji，AN Lian-suo.De-noising technique for vibration signals of rotating machinery based on mathematical morphology filter[J].Chinese Journalof Mechanical Engineering，2006，42(4):127 －130.

[6]沈 路，楊富春，周曉軍，等.基于改進EMD與形態濾波的齒輪故障特征提取[J].振動與沖擊，2010，29(3):154－157，211.SHEN Lu，YANG Fu-chun，ZHOU Xiao-jun，et al.Gear fault feature extraction based on improved EMD and morphological filter[J].Journal of Vibration and Shock，2010，29(3):154－157，211.

[7]趙春暉.數學形態濾波器理論及其算法研究[D].哈爾濱:哈爾濱工業大學，1998.

[8]Maragos P，Schafer R W.Morphological filters-partⅠ:their set theoretic analysis and relation to linear shift invariant filters[J].IEEE Trans on ASSP，1987，35(8):1153 －1169.