聲振系統中高頻能量流分析法研究進展

游 進，孟 光，李鴻光

(1.中國空間技術研究院 載人航天總體部，北京 100094;2.上海交通大學 機械系統與振動國家重點實驗室，上海 200240)

出于經濟性要求和減重的考慮，很多產品結構(如汽車、船舶、航空航天器等)采用很多輕薄構件，使得這類結構的中高頻減振降噪問題顯得較為突出。目前廣泛應用于預測復雜結構聲振響應的成熟手段主要包括以力和位移為基本變量的有限元/邊界元法［1－2］，以及以能量為研究變量的統計能量分析法［3－6］(Statistical Energy Analysis，SEA)。對于傳統的有限元/邊界元法，由于結構在中高頻上的模態波長很小，聲振響應建模分析需要劃分非常細密的網格，造成計算成本過高。此外，中高頻上，結構參數、邊界條件及載荷的細微變化均會對結構的位移響應造成顯著影響，傳統的有限元/邊界元法作為一種確定性方法，其計算結果只能視為聲振系統所有可能動力響應集合的一個樣本，這進一步反映出有限元/邊界元在中高頻應用上的局限性。SEA法基于結構動力分析的模態方法提出，以耦合結構子系統的空間及頻率平均總能量為基本研究變量，并從能量存儲、傳遞和耗散的角度來描述結構的動力行為。SEA采用集總參數模型，所建立的模型規模較小，對于復雜結構，只需用一組線性代數方程便可反映耦合子系統間的能量平衡關系，求解方程便可得到所有子系統的穩態振動能量，因而方法的計算效率很高。經典SEA法的不足之處在于其引入的假設過于苛刻，因此一直以來都有學者質疑其合理性［7－9］，同時這些假設也將SEA法的適用范圍限制在高頻區域。

為克服現有動力響應預測方法的局限性，學者們基于結構動力分析的波動方法提出了能量流分析法(Energy Flow Analysis，EFA)。能量流分析法基于對結構內傳播波功率流傳遞特性的認識，以在時間和波長距離上平均的能量密度及功率流作為其基本研究變量。通過利用三個基本關系，即:① 簡化的功率流－能量密度關系;② 損耗功率－能量密度關系;③ 微元體的能量守恒，可以導出能量流分析法的控制微分方程。能量流分析法以能量密度為變量，因此可以反映動力響應在耦合子系統空間上的分布情況，這與SEA作為集總參數方法只能提供子系統的平均總能量相比，具有很大的優越性。從應用的角度，能量流分析法可以方便地利用有限元法基于聲振系統的幾何模型對能量密度場進行建模求解，相比于SEA不關注子系統的幾何模型細節及載荷位置等信息，能量流分析法可充分地反映幾何特征及載荷位置等對聲振系統動響應的影響。由于能量流分析法實用上有很大的優點且方法引入的假設條件較少，因此受到很大的關注，提出至今獲得了很大的發展，本文基于能量流分析法理論及應用研究的相關文獻，系統回顧能量流分析法的發展過程，提煉該方法的理論框架并說明其研究進展。

1 基本能量流分析方程的發展

俄羅斯的一些學者最早從考慮能量密度和功率流在結構內分布的角度來研究結構的動響應問題［10－14］。在這些有關結構內能量流傳遞特性的早期研究中，結構中不同類型的傳播波被假定為互不相干且它們的能量可以疊加，從而導出了類似于熱傳導的描述結構內能量流分布的微分方程:

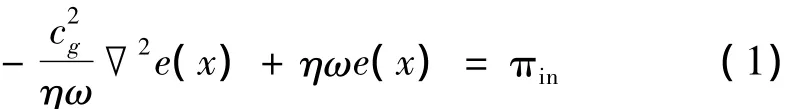
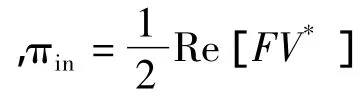
Wohlever等［16］針對縱向振動桿和橫向振動梁進一步研究了穩態振動結構內的能量傳遞特性與熱傳導問題的類比性，并揭示了導出能量流分析微分方程所做近似假設的物理含義。假定桿內存在相向傳播的縱波，在小阻尼條件下，由振動位移解導出的相向傳播波的功率流和能量密度的解析式表明，功率流與能量密度的梯度成正比，能量由高能量密度區域流向低能量密度區域，即:

式中，q表示同時存在正負向傳播波的桿內功率流。式(2)在桿上任意一點均成立，不需做任何假設。對于梁的彎曲振動，由位移解導出的功率流與能量密度解析式表明，類似于式(2)的規律在任意點上并不準確成立，只有忽略了彎曲振動的近場項并將功率流與能量密度在一個波長的局部空間范圍上進行平均，才可得到如式(2)的功率傳遞特性表達式。在波長距離上對解析能量密度和功率流進行平均是一種重要的概念，因為經過空間周期平均后，相同頻率的相向傳播波的能量密度和功率流等能量變量可以進行疊加，從而使得從能量角度來理解振動問題變得簡單。由于這種空間上的周期平均不涉及其它前提假設，因而實質上反映了結構遠場傳播波穩態功率傳遞特性的一般規律。

基于對結構內功率流傳遞基本規律的認識，Bouthier等［17－20］求得了板彎曲振動和張緊膜在時間及波長距離上平均的功率流及能量密度表達式，同時也導出了相應的能量微分方程:

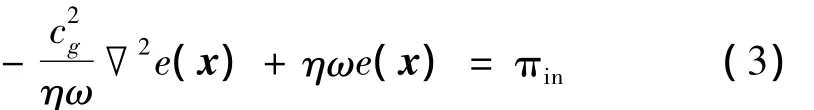
式中:cg為二維結構相應傳播波的群速，x為二維結構任意點的位置矢量。上式的導出利用了二維結構內相向平面彎曲波及壓縮波的如下簡化功率流傳遞特性:

式中，q為二維結構內的功率流矢量。板的彎曲振動及張緊膜的能量方程均通過與從結構運動方程出發用模態分析法解得的能量響應精確解進行了對比，從而驗證了能量流分析法的有效性。在Bouthier等相關研究的基礎上，Ichchou［21］對考慮柱面波、球面波和平面波時的能量傳遞模型進行了一般性總結。

Zhang等［22－23］提出了一種新的推導結構能量流分析微分方程的方法，這種方法視結構中任意方向上的傳播波為在兩個垂直方向上傳播的波的疊加，合成波的能量密度及功率流均由傳播方向互相垂直的兩個波的能量密度及功率流疊加而成，因而可單獨對傳播方向垂直的兩個波的能量傳遞特性進行分析，這樣做簡化了能量流分析微分方程的推導。

Lase等［24］期望提供從能量角度出發描述結構振動的一般性認識，提出了通用能量動力學方法(General Energetic Method，GEM)。這種方法指出結構內分別存在兩種能量密度和功率流，其中一種對應于結構的總能量密度和主動能量流(active energy flow)，反映結構內傳播波的能量特性，另一種對應于Lagrangian能量密度和被動能量流(reactive energy flow)，反映結構的模態能量特性。兩種不同類型的能量密度和能量流均存在控制微分方程，而當忽略近場效應和在波長距離上平均，即可由GEM中描述總能量和主動能量流的方程導出經典的能量流微分方程式(1)。

薄板結構面內縱波和剪切波的能量微分方程由Park等導出［25］，其形式與式(3)一致。由于縱波和剪切波的位移在運動方程中相互耦合，因此，與確立彎曲波的能量傳遞模型相比，面內波能量傳遞模型的確立較為復雜。通過引入兩個勢函數使運動方程所描述的縱向運動和剪切運動解耦，分別導出縱波和剪切波的能量密度和功率流表達式并在一個波長的空間距離進行局部平均，仍可以得到與式(4)一致的簡化功率流傳遞特性。

解妙霞等［26］導出了圓柱殼在軸對稱激勵下的彎曲振動能量微分方程，由于激勵的對稱性，所考慮的圓柱殼彎曲運動屬一維問題，因而相應的能量微分方程的形式和梁的彎曲振動能量微分方程一致。

對于在垂直方向上具有不同剛度的正交各向異性板，Park等［27］導出了其彎曲波場的能量流分析方程:

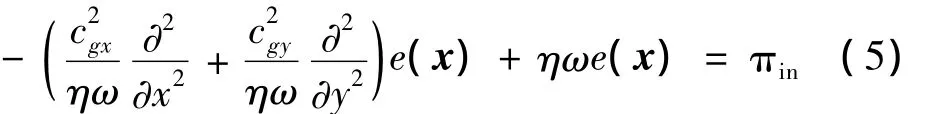
式中:cgx和cgy為相互垂直方向上的彎曲波群速。當考慮板為各向同性時，能量方程式(5)簡化為式(3)。正交各向異性板的功率流與能量密度關系為:

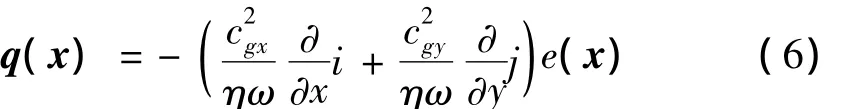
可見功率流與能量密度的梯度并不直接相關。

薄板彎曲波場能量方程式(3)是基于經典的Kirchhoff板理論導出的，Kirchhoff板理論只用板中面的撓度描述板的運動狀態，而在高頻上彎曲板的剪切變形和轉動慣量的效應非常顯著，需用Mindlin板理論對其動力狀態進行描述，基于此，Park等［28］導出了均勻Mindlin板的彎曲振動能量流分析方程。在Mindlin板的臨界頻率以下，板的彎曲振動以撓曲效應為主，其能量方程式與式(3)一致。在Mindlin板的臨界頻率以上，彎曲振動板包含三種傳播波，即面外剪切波(Outof-plane shear wave)，撓曲主導彎曲波(Bending dominant flexural wave)和剪切主導彎曲波(Shear dominant flexural wave)，利用能量流分析理論的空間局部平均的思想，對這三種波場均可導出與式(3)形式一致的能量方程。

Yan［29］研究了能量流分析法在復合層板上的應用，復合層板由多層正交各向異性板以不定向角度層疊而成。由于復合層板為各向異性，傳播波的群速呈現各向不同的特點，在假定結構波場為平面波散射波場后，Yan導出了復合層板的彎曲、縱向及剪切波場的能量微分方程:

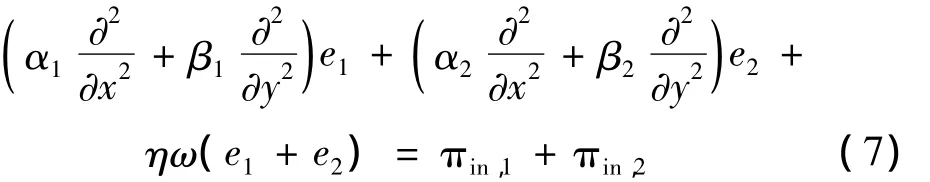
式中:α1，α2，β1和 β2與結構剛度、頻率及波數有關。式(7)中，復合層板結構的波場能量為兩部分能量之和，對其中的單一能量組分，均存在與之對應的功率流組分，兩者間符合與式(4)一致的能量傳遞關系。

一般地，各種波場的能量流微分方程均利用有限元法求解，很多文獻把能量流分析方程的有限元求解方法稱為能量有限元分析(Energy finite element analysis，EFEA)。為簡化計算，Wang 等［30－32］提出用有限體元法求解能量流分析的基本方程，并稱之為零階能量有限元分析(EFEA0)。該方法的思路是用有限體元對連續能量場進行離散，在單個體元空間上對能量方程進行積分，同時用相鄰體元能量的差分代替能量對位置的導數，得到單個體元的能量平衡方程，這一過程消除了原方程中能量變量對位置的二階微分。Santos［77，78］等采用譜元法求解基本能量流分析方程，提出了能量譜有限元法(Energy spectral element method，ESEM)，該方法可給出能量分析方程的解析解，但適用性有限，很難用于幾何非均勻結構和任意邊界條件等一般性問題。

2 耦合形式下能量流分析的應用

工程實際中需進行中高頻動響應分析的聲振系統一般都是較為復雜的耦合系統，可能包含不同子結構間，或結構與流體間的復雜耦合形式。在基本構件的能量微分方程提出后，能量流分析法首先被用于一般的耦合結構上，后又被用于處理結構與流體(包括聲場與液體)間的耦合和其它更為復雜的結構耦合形式上。

能量流分析法的基本變量是經空間局部平均的能量密度，因而在耦合結構交界面兩邊的能量密度不連續。能量流分析法提出后遇到的首要問題是不能將其有效地應用于一般耦合結構，在其發展初期的大多數應用都只針對共線耦合梁等簡單耦合情況［16，24，33－34］。要將能量流分析法用于求解一般耦合結構，關鍵性問題將連接處的功率流傳遞特性與能量流分析的基本理論進行結合。考慮結構間的耦合關系并將能量流分析法應用于一般耦合結構的方法由Cho等人提出［35－38］，具體過程就是將連接處各波場的能量密度和功率流均視為正負向傳播波的能量密度之和和功率流之差，再結合半無限耦合連接的功率傳遞系數，將連接處各耦合波場的能量密度與功率流聯系起來，從而使結構耦合問題得以解決。

Bernhard等［39］總結了將能量流分析應用于一般耦合結構的具體方法，對一個復雜耦合板結構的能量響應進行計算以展示這種方法在處理實際復雜問題上的可行性。Vlahopoulos等［40］基于能量流分析法對復雜船體結構的中高頻響應進行了預測。Klos對一個由不同材料組成的共面耦合板的能量響應進行了計算［41］。Borlase等［42］基于能量流分析法對大型復雜結構的阻尼分布進行優化，以達到控制結構某一部分振動能量的目的。Park等［25］對兩塊耦合矩形板的能量響應進行求解，計算中考慮了面內縱波、剪切波與彎曲波的相互耦合，結果表明，當阻尼很大且分析頻率很高時，面內波的能量響應水平與彎曲波的能量響應水平相當。Zhang等［22－23］利用能量流分析法對一個潛艇結構以及小型漁船的能量響應進行了計算，并將結果與用致密有限元網格模型計算的響應以及SEA的計算結果進行了比較，對于分析結構的一些構件，能量流分析法的結果與其它方法的預測結果比較吻合。曾勤謙等［43］利用能量流分析法對一個平面框架結構進行響應預測。孫麗萍等［44－45］將能量流分析法用于船體基座的動響應計算。吳軼鋼基于零階能量有限元分析對加筋板的能量響應進行了求解［46］。

Cho等［35－38］提出的處理耦合結構的方法雖然主要針對由相同結構件組成的耦合系統(如僅由梁或板組成的耦合系統)，但其反映了能量流分析法處理不同波場間耦合問題的一般原理，在其基礎上，很多學者作了不同方面的研究，以將能量流分析法的應用拓展至更為一般的耦合形式。Seo等［47］研究了能量流分析法在通過梁連接的耦合板結構上的應用，并對一個含等距排列加強筋的矩形板的能量響應進行求解，與位移解的對比驗證了方法的正確性。Vlahopoulos［48－50］將能量流分析法與周期結構理論相結合，對用周期布置的加強筋強化的潛艇結構的動力響應進行了求解并與試驗結果進行了對比。

為基于能量流分析法處理聲振耦合問題，Bitsie［51］首先導出了聲場的能量流分析方程，并在其基礎上導出了結構與聲場間的耦合關系。聲場的能量流分析方程與式(1)式(3)的形式相同，只是其位置矢量為空間三維矢量，聲場的功率流也相應地為空間三維矢量。對于彎曲振動平板與聲場間的耦合問題，當頻率低于板的臨界聲輻射頻率時，結構－聲場的耦合關系對平板的作用表現為板上的有效面質量和聲輻射阻尼因子，其中聲輻射阻尼因子是考慮到有限板的邊界聲輻射而引入的修正項;當頻率高于板的臨界聲輻射頻率時，該耦合關系對平板的作用表現為板上的輻射阻尼因子。考慮了結構－聲場耦合關系的結構能量微分方程為:

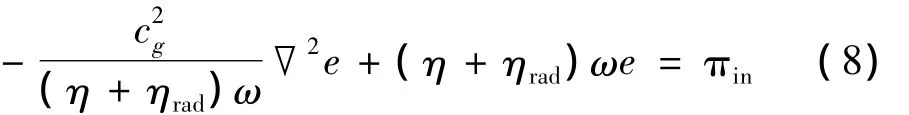
式中，cg為板中彎曲波的群速，當頻率低于臨界聲輻射頻率時，其值受到等效面質量的影響，ηrad為結構－聲場間的耦合作用導致的輻射阻尼因子，其表達式為:

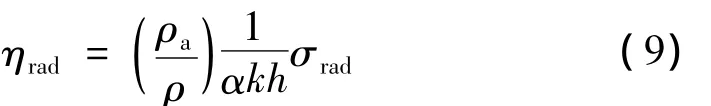
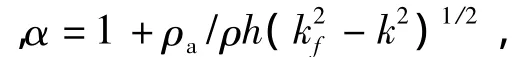
結構－聲場間的耦合問題還可利用基于能量流分析與能量邊界元分析的混合方法進行處理［54－55］，對于由噪聲源引起的結構高頻振動，可以通過能量邊界元法的計算結果得到噪聲源作用于結構的激勵，并由此根據能量流分析法計算結構響應。Dong等［56］基于該方法對聲振系統的振動及噪聲對設計參數的敏感度進行研究，并在其基礎上進行優化設計，相關方法被用于汽車及船舶的結構設計，以使結構的高頻噪聲達到最小。

Zhang等［22，57］研究了能量流分析法在與液體接觸的彎曲振動板結構上的應用，與該方法在結構－聲場耦合情況下的應用相似，液體與結構間的耦合作用也是根據頻率的不同以等效面質量或等效輻射阻尼因子的方式對板的動力特性產生影響，此種情況下，板的能量方程與式(8)相似。由于液體與板間的耦合作用會表現為板結構上的等效面質量，因此與板接觸的液體也會改變耦合板結構連接的功率傳遞特性。此外，他們進一步地將考慮了接觸流體作用的能量流分析法應用在一些更復雜的耦合結構上，即還同時考慮了周期排布加強筋或多塊板通過公共梁耦合的情況［58－59］，并將其用于預測與流體接觸的潛艇外殼的動力響應。

在一定的頻率范圍內，實際耦合結構的一部分子結構可能只包含少數幾個波長(這些結構件稱為短件或剛件)，而另一部分子結構可能包含大量波長(這些結構件稱為長件或柔件)。考慮到這類結構中的短件適合用基于位移的傳統有限元法求解，為預測整個耦合結構的響應，Vlahopoulos等［60－62］提出了結合能量流分析與傳統有限元法的混合方法。該方法的主要思路是用動力縮聚得到短件在邊界自由度上位移與力間的關系，再考慮力和位移的連續性條件將短件與長件進行耦合。這種方法主要被用來對由短梁連接的兩根長梁這一共線耦合梁結構的動力特性進行研究［60－61］。當外載荷作用在長件上時，可以根據短件的動力縮聚模型及邊界適應性條件計算出連接短件的功率傳遞特性，依此功率傳遞特性用能量流分析法計算長件的能量響應分布并由此確定短件邊界上的響應，最后再計算短件的位移響應。當有激勵作用在短件上時［62］，短件自身的響應會影響其所代表的連接的功率傳遞特性，因此需要根據邊界適應性條件通過迭代來確定連接特性。這種方法后來被進一步推廣應用到平面復雜耦合梁結構上［63］，并考慮了梁連接處彎曲波與縱波間的耦合。由于在計算短件連接的功率流傳遞特性需利用長件中傳播波的解析式，而實際中無法假定具有一般幾何特征的長件中傳播波的解析式，因此Vlahopoulos等人提出的這種方法局限于應用在平面梁、桿耦合結構上。

為解決一般的剛、柔件耦合結構的響應預測問題，利用模糊結構理論的基本思想［64－66］，Hong 等［67］提出了另一種能量流分析/有限元混合方法。該方法以附加阻尼的方式反映柔件對剛件動響應的影響，其數值基于柔件在連接處的阻抗獲得。該方法具體過程是首先通過基于位移的傳統有限元法計算剛件的動響應并計算消耗在附加等效阻尼上的功率，以此作為柔件的輸入功率，再利用能量流分析法計算柔件上的能量密度分布。利用該方法，Hong等人對多個梁板組合結構的動響應進行了計算。與Vlahopoulos等先前提出的混合方法相比［60－62］，這種方法具有更廣泛的適用性。

3 結構的隨機能量流分析

能量流分析法提出后在很多實際問題中得到了應用，但是大部分的研究及應用都是針對結構受單頻激勵的情形，這與能量流分析法的基本原理有關。在推導各種基本結構件及聲場的能量流分析基本方程的過程中，均是在假定單頻激勵激發起單頻傳播波的情況下，得到了各波場的時間—空間平均功率流與能量密度間的簡明關系。實際結構在中高頻上所受的激勵在很多情況下都是寬帶隨機激勵的形式，對于隨機激勵下結構的響應預測過去，能量流分析法的應用方式主要有兩種:① 按單頻激勵形式計算結構在分析帶寬內多個頻率點處的能量響應再對響應進行頻率平均;②只在激勵帶寬的中心頻率上預測結構的動力響應。然而，以上兩種有關能量流分析法處理隨機激勵情形的應用在實質上并沒有求解結構在隨機激勵下的響應，其計算結果并不反映結構在隨機激勵下的絕對響應能量水平。

對于隨機激勵下能量流分析法的應用，Han等［68－69］曾進行過相關研究。他們導出了單根梁及單塊板在隨機激勵下能量密度的模態分析解析解，同時基于傳統的能量流分析法計算結構響應，通過譜積分的方式得到平均能量密度，并主要對結構在較低頻的一個頻段內的結構能量響應進行分析。Han等所給出的方法應用屬于半經驗性質，未經嚴格的推導及證明，很少有后續相關研究及應用。

通過考慮隨機激勵下結構能量方程中輸入功率的表達形式，游進等［70－74］針對梁及板結構系統提出了能量流分析在隨機激勵下的應用方法，并稱之為隨機能量流分析(Random energy flow analysis，REFA)。以彎曲振動板為例，穩態隨機激勵下，板的隨機能量流分析方程為:

式中，Πin(x，ω)為穩態隨機激勵的輸入功率譜，E的物理意義為結構能量密度響應譜的空間局部平均值［74］。相應的平均能量密度及功率流分別按以下兩式計算:

隨機能量流分析方程(10)建立了結構在隨機激勵下的能量密度響應譜與激勵輸入功率譜間的關系，其相應的平均能量密度及功率流均需通過對譜進行積分得到(即式(11)、式(12))，這是其應用上與傳統能量流分析法處理單頻激勵情形的不同之處。此外，由于隨機激勵下的結構響應是非確定性響應，因此隨機能量流分析法的計算結果反映的是結構隨機能量響應的統計平均值。

隨機能量流分析法提出后被用于計算受隨機激勵的平面框架結構［70］、空間框架結構［71］及耦合板結構［72－73］的能量響應及功率流。游進等［75］將隨機能量流分析法用于計算受隨機激勵的單根梁的能量密度和功率流，并通過與模態分析精確解進行對比，表明分析頻帶所包含的模態數而非常寬是影響該方法預測精度的重要因素，在分析頻帶模態數足夠大的情況下，該方法可以在廣闊的頻率范圍上有效預測單系統的能量密度及功率流。

能量流分析和SEA都是基于能量的動力響應預測方法，兩種方法間必然存在一定的聯系。SEA由于采用的是受獨立噪聲激勵的線性保守耦合振子的功率傳遞模型［3］，且由于其所采用的基本假設的關系，適于求解受非相關隨機激勵的耦合結構的動響應［4］，其求解結果反映的是耦合結構隨機激勵下的穩態響應。傳統的能量流分析法主要用于計算單頻激勵下的動力響應，因此在過去的研究中，兩種方法間并未建立起直接聯系，兩種方法計算結果的對比從未直接針對子系統的能量響應，而是間接地針對不同子系統響應能量的比值［23，40，57，76］。考慮到隨機能量流分析可計算耦合結構在隨機激勵下的能量響應，游進等［74］以耦合梁結構為模型建立了隨機能量流分析與SEA間關于能量和功率流變量間的直接關系。

隨機能量流分析與SEA雖分別從波及模態的角度定義各自的子系統，但它們所定義的子系統從本質上是一致的，若用兩種方法對同一耦合結構進行分析，則對相同的子系統，兩種方法預測的子系統總能量應近似相等，即:

隨機能量流分析與SEA所描述的子系統間功率流的不同點體現在兩點上:① SEA是集總參數方法，其計算的功率流為集總參數，隨機能量流分析建立分布式模型，可以預測功率流在子系統內的分布，而只有子系統邊界上的功率流直接反映了耦合子系統間的功率傳遞作用;② SEA與隨機能量流描述的子系統間功率流的方式有所不同:SEA處理的是任意一對耦合子系統間的功率流，隨機能量流分析只給出流入或流出某個子系統的功率流而不區分流入功率的來源和流出功率流的接受源。

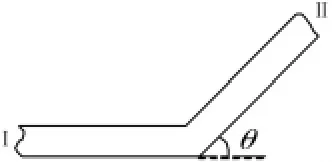
圖1 平面耦合梁結構Fig.1 Planar beam junction

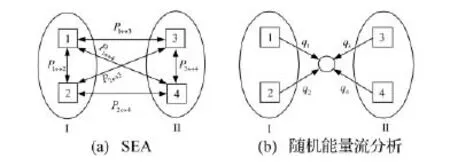
圖2 功率流模型Fig.2 Energy flow models

隨機能量流分析與SEA間關于功率流變量間的關系可以平面耦合梁(如圖1)為模型進行說明。該耦合結構包含彎曲波與縱波間的耦合，以子系統1和2代表梁I的彎曲波和縱波子系統，以子系統3和4代表梁II的彎曲波和縱波子系統，則隨機能量流分析和SEA所采用的功率流模型如圖2所示。圖中Pi?j是SEA計算的子系統i與j間功率流的大小。qi是隨機能量流分析法預測的子系統i在其與其它子系統耦合邊界上的功率流。根據圖2，可得到兩種方法預測的子系統間功率流的關系為:

式(13)、式(14)反映了隨機能量流分析和SEA所定義的響應能量及功率流變量的不同點，同時也建立了兩種方法關于能量和功率流變量間的直接關系，實質上是將兩種方法從研究變量的角度進行統一。基于此，對于任意受隨機激勵的耦合結構，可對兩種方法計算的能量響應和功率流進行直接對比分析。

此外，文獻［71］針對一維結構的功率流特性指出，隨機能量流分析反映的彎曲波場功率流特性與SEA中的耦合振子間的功率流特性是相似的，而前者所反映的縱波場及扭轉波場的功率流特性則無法由后者所采用的耦合振子功率流特性表達。

4 結論

經過二十多年的發展，能量流分析的相關研究獲得了較大進展。基本結構件及一些復合結構的各種波場及聲場的能量流分析基本方程已被建立起來。對于聲振耦合系統，能量流分析法不僅可用于存在不同波場間耦合的復雜耦合結構上，而且可以預測結構－流體耦合系統的動力響應，還可與其它方法相結合以處理一些具體的復雜耦合問題，體現出能量流分析法良好的適用性。此外，隨機能量流分析法解決了隨機激勵下聲振系統能量密度響應及功率流的計算問題，同時，隨機能量流分析與經典SEA間的區別和理論關聯也在一定程度上得到確認。目前，能量流分析理論的一個不足是方法特性研究還不夠深入完善，需要進一步系統研究影響方法使用范圍和預測精度的各種因素，以便于方法的廣泛應用。

［1］ Banerjee P K，Butterfield R.Boundary Element Methods in Engineering Science［M］.UK:McGraw-Hill Book Company，1981.

［2］Zienkiewicz O C，Taylor R L.The finite element method volume 1: the basis［M］. Boston: Butterworth-Heinemann，2000.

［3］Lyon R H，DeJong R G.Theory and application of statistical energy analysis ［M］. Boston: Butterworth-Heinemann，1995.

［4］ Fahy F J.Statistical energy analysis:a critical overview［J］.Philosophical Transactions of the Royal Society:Physical and Engineering Sciences，1994，346(1681):431 －447.

［5］ Heckl M，Lewit M.Statistical energy analysis as a tool for quantifying sound and vibration transmission paths［J］.Philosophical Transactions of the Royal Society:Physical and Engineering Sciences，1994，346(1681):449－464.

［6］ Heron K H.Advanced statistical energy analysis［J］.Philosophical Transactions of the Royal Society:Physical and Engineering Sciences，1994，346(1681):501－510.

［7］ Mace B R.On the statistical energy analysis hypothesis of coupling power proportionality and some implications of its failure［J］.Journal of Sound and Vibration，1994，178(1):95－112.

［8］ Fahy F J.Statistical energy analysis:a wolf in sheep＇s clothing［C］. Proceedings of the Internoise. Leuven，Belgium，1993.

［9］Culla A，Sestieri A.Is it possible to treat confidentially SEA the wolf in sheep＇s clothing［J］.Mechanical Systems and Signal Processing，2006，20(6):1372－1399.

［10］Belov V D，Rybak S A.Applicability of the transport equation in the one-dimensional wave-propagation problem［J］.Journal of Soviet Physics Acoustics，1975，21(2):110－114.

［11］Belov V D，Rybak S A，Tartakovskii B D.Propagation of vibrational energy in absorbing structures［J］.Journal of Soviet Physics Acoustics，1977，23(2):115 －119.

［12］ Buvailo L E，Ionov A V.Application of the finite element method to the investigation of the vibroacoustical characteristics of structures at high frequency［J］.Journal of Soviet Physics Acoustics，1980，26(4):277 －279.

［13］ Butlitskaya I A，Vyalyshev A I，Tartakovskii B D.Propagation of vibrational and acoustic energy along a structure with losses［J］.Journal of Soviet Physics Acoustics，1983，29(4):333－334.

［14］ Nikiforov A S.Estimating the intensity of structure-borne noise in ribbed structures［C］.Proceedings of the 3rd international congress on intensity techniques， Senlis，France，1990.

［15］ Nefske D J，Sung S H.Power flow finite element analysis of dynamic systems:Basic theory and application to beams［J］.Journal of Vibration，Acoustics，Stress，and Reliability in Design，1989，111(1):94－100.

［16］ Wohlever J C，Bernhard R J.Mechanical energy flow models of rods and beams［J］.Journal of Sound and Vibration，1992，153(1):1－19.

［17］ Bouthier O M，Bernhard R J.Simple models of energy flow in vibrating membranes［J］.Journal of Sound and Vibration，1995，182(1):129－147.

［18］ Bouthier O M，Bernhard R J.Simple models of the energetics of transversely vibrating plates［J］.Journal of Sound and Vibration，1995，182(1):149－164.

［19］ Bouthier O M.Energetics of vibrating systems［D］.Purdue University，1992.

［20］ Bouthier O M，Bernhard R J.Models of space-averaged energetics of plates［J］.AIAA Journal，1992，30(3):616 －623.

［21］ Ichchou M N，Jezequel L.Comments on simple models of the energy flow in vibrating membranes and on simple models of the energetics of transversly vibrating plates［J］.Journal of Sound and Vibration，1996，195(4):679－685.

［22］Zhang W.Energy finite element method for vibration analysis of stiffened plates under fluid loading［D］.University of Michigan，2003.

［23］Zhang W，Wang A，Vlahopoulos N.An alternative energy finite element formulation based on incoherent orthogonal waves and its validation for marine structures［J］.Finite Elements in Analysis and Design，2002，38(12):1095－1113.

［24］Lase Y，Ichchou M N，Jezequel L.Energy flow analysis of bars and beams:theoretical formulations［J］.Journal of Sound and Vibration，1996，192(1):281－305.

［25］ Park D H，Hong S Y，Kil H G，et al.Power flow model and analysis of in-plane waves in finite coupled thin plates［J］.Journal of Sound and Vibration，2001，244(4):651 －668.

［26］解妙霞，陳花玲，吳九匯.圓柱殼高頻彎曲振動的能量有限元分析［J］.西安交通大學學報，2008，42(9):1113－1116.

［27］Park D H，Hong S Y，Kil H G.Vibrational energy flow models of finite orthotropic plates［J］.Shock and Vibration，2003，10(2):97－113.

［28］ Park Y H，Hong S Y.Vibrational power flow models for transversely vibrating finite Mindlin plate［J］.Journal of Sound and Vibration，2008，317(3－5):800－840.

［29］ Yan X.Energy finite element analysis developments for high frequency vibration analysis of composite structures［D］.The University of Michigan，2008.

［30］ Wang S.High frequency energy flow analysis methods:Numerical implementation，applications，and verification［D］.Purdue University，2000.

［31］ Wang S，Bernhard R J.Theory and applications of a simplified energy finite element method and its similarity to SEA［J］.Noise Control Engineering Journal，2002，50(2):63 －72.

［32］ Marburg S，Nolte B.Computational acoustics of noise propagation in fluids-finite and boundary element methods［J］.Germany:Springer Berlin Heidelberg，2008.

［33］ Stiehl A L.Power flow analysis of beam members with multiple wave types［J］.Finite Elements in Analysis and Design，1996，21(4):253－264.

［34］ Nefske D J，Sung S H.Power flow finite element analysis of dynamic systems:basic theory and application to beams［J］.Journal of Vibration，Acoustics，Stress，and Reliability in Design，1989，111(1):94－100.

［35］ Cho P E.Energy flow analysis of coupled structures［D］.Purdue University，1993.

［36］ Cho P E，Bernhard R J.A simple method for predicting energy flow distribution in frame structures［C］.in Proceedings of the 4th International Congress on Intensity Techniques.Senlis，France，1993.

［37］ Cho P E，Bernhard R J.Energy finite element method for coupled structures［J］.Yokohama，Japan，1994.

［38］ Cho P E，Bernhard R J.Energy flow analysis of coupled beams［J］.Journal of Sound and Vibration，1998，211(4):593－605.

［39］ Bernhard R J，Huff J E.Structural-acoustic design at high frequency using the energy finite element method［J］.Journal of Vibration and Acoustics，Transactions of the ASME，1999，121(3):295－301.

［40］Vlahopoulos N，Garza-Rios L O，Mollo C.Numerical implementation，validation，and marine applications of an energy finite element formulation［J］.Journal of Ship Research，1999，43(3):143－156.

［41］ Klos J.Modeling point excited plates using an energy finite element method［C］.The 2004 National Conference on Noise Control Engineering［J］.Baltimore，Maryland，2004.

［42］Borlase G A，Vlahopoulos N.Energy finite element optimization process for reducing high-frequency vibration in largescale structures［J］.Finite Elements in Analysis and Design，2000，36(1):51－67.

［43］曾勤謙，華宏星，韓祖舜.耦合結構中的功率流有限元法［J］.上海交通大學學報，2000，34(4):503－506.

［44］孫麗萍，聶 武.能量有限元法在船舶結構中的應用［J］.哈爾濱工業大學學報，2008，40(9):1491－1494.

［45］孫麗萍.能量有限元法研究及其應用［D］.哈爾濱:哈爾濱工程大學，2004.

［46］吳軼鋼.零階能量有限元方法及其在船舶結構聲輻射中的應用研究［D］.武漢:武漢理工大學，2008.

［47］Seo S H，Hong S Y，Kil H G.Power flow analysis of reinforced beam-plate coupled structures［J］.Journal of Sound and Vibration，2003，259(5):1109－1129.

［48］ Vlahopoulos N.Energy finite element analysis for computing the high frequency vibration of the aluminum testbed cylinder and correlating the results to test data［J］.NASA/CR-2005－213760，2005.

［49］ Vlahopoulos N，Wang A，Wu K.An EFEA formulation for computing structural response of complex structures［C］.Proceedings of ASME 2005 International Mechanical Engineering Congress and Exposition.Orlando，USA，2005.

［50］Zhang G，Vlahopoulos N.Validation of an EFEA formulation for computing the vibrational response of complex structures［C］.Proceedings of 2007 SAE Noise and Vibration Conference.Traverse city，USA，2007.

［51］ Bitsie F.The structural-acoustic energy finite-element method and energy boundary-element method［D］.Purdue University，1996.

［52］ Dong J，Choi K K，Wang A，et al.Parametric design sensitivity analysis of high-frequency structural-acoustic problems using energy finite element method［J］.International Journal for Numerical Methods in Engineering，2003，62(1):83－121.

［53］ Moens I，Vandepitte D，Sas P.Vibro-acoustic energy flow models implemented by finite elements［M］.Leuven，Belgium，1998.

［54］Vlahopoulos N，Zhang G，He J.Combining an energy boundary element with an energy finite element analysis for airborne noise simulations［C］.Proceedings of 2007 SAE Noise and Vibration Conference.Traverse City，USA，2007.

［55］Vlahopoulos N，Li S，Sun J.Combining energy boundary element and energy finite element simulations for airborne noise analysis［J］.Proceedings of 2006 ASME International Mechanical Engineering Congress and Exposition.Chicago，Illinois，USA，2006.

［56］ Dong J，Choi K K，Vlahopoulos N，et al.Sensitivity analysis and optimization using energy finite element and boundary element methods［J］.AIAA Journal，2007，45(6):1187 －1198.

［57］ Zhang W，Wang A，Vlahopoulos N，et al.High-frequency vibration analysis of thin elastic plates under heavy fluid loading by an energy finite element formulation［J］.Journal of Sound and Vibration，2003，263(1):21－46.

［58］ Zhang W，Wang A，Vlahopoulos N，et al.A vibration analysis of stiffened plates under heavy fluid loading by an energy finite element analysis formulation［J］.Finite Elements in A-nalysis and Design，2005，41(11－12):1056－1078.

［59］ Zhang W，Vlahopoulos N，Wu K.An energy finite element formulation for high-frequency vibration analysis of externally fluid-loaded cylindrical shells with periodic circumferential stiffeners subjected to axi-symmetric excitation［J］.Journal of Sound and Vibration，2005，282(3－5):679－700.

［60］ Vlahopoulos N，Zhao X.Basic development of hybrid finite element method for midfrequency structural vibrations［J］.AIAA Journal，1999，37(11):1495 －1505.

［61］Vlahopoulos N，Zhao X.An investigation of power flow in the mid-frequency range for systems of co-linear beams based on a hybrid finite element formulation［J］.Journal of Sound and Vibration，2001，242(3):445－473.

［62］Zhao X，Vlahopoulos N.A hybrid finite element formulation for mid-frequency analysis of systems with excitation applied on short members［J］.Journal of Sound and Vibration，2000，237(2):181－202.

［63］ Zhao X，Vlahopoulos N.A basic hybrid finite element formulation for mid-frequency analysis of beams connected at an arbitrary angle［J］.Journal of Sound and Vibration，2004，269(1－2):135－164.

［64］ Soize C.A model and numerical method in the medium frequency range for vibroacoustic predictions using the theory of structural fuzzy［J］.Journal of the Acoustical Society of A-merica，1993，94(2):849 －865.

［65］ Soize C.Reduced models in the medium-frequency range for general external structural-acoustic systems［J］.Journal of the Acoustical Society of America，1998，103(3):3393－3406.

［66］ Soize C，Bjaoui K.Estimation of fuzzy structure parameters for continuous junctions［J］.Journal of the Acoustical Society of America，2000，107(4):2011－2020.

［67］Hong S B，Wang A，Vlahopoulos N.A hybrid finite element formulation for a beam-plate system［J］.Journal of Sound and Vibration，2006，298(1－2):233－256.

［68］ Han F，Bernhard R J，Mongeau L G.Energy flow analysis of vibrating beams and plates for discrete random excitations［J］.Journal of Sound and Vibration，1997，208(5):841－859.

［69］ Han F，Mongeau L G，Bernhard R J.Energy flow analysis of beams and plates for random distributed loading［J］.Journal of Fluids and Structures，1998，12(3):315 －333.

［70］游 進，孟 光，李鴻光，等.隨機激勵下框架梁結構能量有限元分析［J］.上海交通大學學報，2009，43(10):1632－1635.

［71］游 進，孟 光，李鴻光.三維框架結構隨機能量流分析［J］.上海交通大學學報，2010，44(8):1150－1154.

［72］游 進，李鴻光，孟 光.耦合板結構隨機能量有限元分析［J］.振動與沖擊，2009，28(11):43－46.

［73］游 進，孟 光，李鴻光.L型耦合板相關激勵下高頻隨機能量流分析［J］.振動工程學報，2010，23(1):60－63.

［74］ You J，Meng G，Li H G.Random energy flow analysis of coupled beam structures and its correlation with SEA［J］.Archive of Applied Mechanics，2011，81(1):37－50.

［75］You J，Li H G，Meng G.Validity investigation of random energy flow analysis for beam structures［J］.Shock and Vibration，2011，18(1－2):269－280.

［76］ Vlahopoulos N，Zhang W.Validation of the EFEA method through correlation with conventional FEA and SEA results［J］.Proceedings of 2001 SAE Noise and Vibration Conference.Grand Traverse，USA，2001.

［77］Santos E R O.High frequency vibration analysis by energy methods［D］.State University of Campinas，2006.

［78］ Santos E R O，Arruda J R F，Dos Santos J M C.Modeling of coupled structural systems by an energy spectral method［J］.Journal of Sound and Vibration，2008，316(1－5):1－24.