基于FFT的擴頻通信系統抗干擾技術研究

張銀蒲，孫茂松，竇桂華

（唐山學院信息工程系，河北唐山063000）

基于FFT的擴頻通信系統抗干擾技術研究

張銀蒲，孫茂松，竇桂華

（唐山學院信息工程系，河北唐山063000）

針對無線信道中的高斯白噪聲、窄帶干擾問題，采用重疊變換的FFT頻域陷波算法對相關干擾進行削弱或消除，并將其在擴頻通信系統中進行了仿真分析。結果表明，這項技術可使受干擾后的頻譜泄露大大降低，從而減少了信號的損傷，提高了信息傳輸的準確性、可靠性。

抗干擾技術；重疊變換的FFT頻域陷波算法；擴頻通信

擴頻通信用擴展頻譜的方法換取較高信噪比，具有較傳統無線通信方式無可比擬的優勢。無線通信系統中信息的傳輸要受到移動無線信道的制約，而信道中不可避免的會存在一些干擾，如果干擾太強，當超出系統的干擾容限時，系統將無法正常工作。擴頻通信系統本身有一定的抗干擾能力，但在有較強干擾的情況下，尤其是在有意的敵對干擾環境下，干擾強度很容易超出其干擾容限［1］，這就需要采取相關技術來增強系統的抗干擾能力，而干擾抑制技術是一種很有效的措施。

1 基于FFT的擴頻通信的信道抗干擾技術

擴頻通信系統中的無線信道是極其復雜的，路徑損失、信號的多徑傳輸以及移動引起的接收信號頻移等都會使信號產生衰落。當然，信道中也會存在一些人為和非人為的干擾。高斯白噪聲就是一種不可避免的噪聲，只能削弱而不能完全消除；窄帶干擾是一種人為加入信道的干擾，它的功率可以特別大，足以淹沒干擾頻段的信號信息，是無線通信的巨大障礙，對此必須進行削弱或消除。

干擾抑制技術通常是利用信號和干擾在時域和頻域的特性差別來檢測和消除干擾。一般來說，在干擾抑制技術中，可利用的信號和干擾信息越多，則獲得的干擾抑制技術性能就越好。［2］

目前常用的干擾抑制技術主要分為基于預測的干擾抑制技術和變換域的干擾抑制技術。其中，變換域干擾抑制技術主要指在變換域進行的干擾信號的檢測和消除，包括基于FFT、基于重疊變換LT、基于時頻域變換的干擾抑制技術。基于FFT的干擾抑制技術具有能有效地對付多音干擾，隨干擾的變化調整迅速，且易于工程實現的優勢，因此，對基于FFT的干擾抑制技術的研究具有重要意義。

1.1 變換域的干擾抑制算法原理

變換域的干擾抑制技術主要是利用窄帶干擾的功率譜集中在很窄的頻帶中，通過傅里葉變換，將干擾映射到很窄的變換域子帶，通過設置閾值和門限檢測出干擾的位置，控制開關將相應的子帶分量置零，從而達到減輕或抑制干擾的目的。其原理圖如圖1所示。

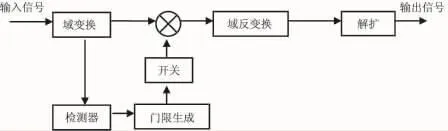
圖1 變換域窄帶干擾抑制原理圖

在變換域抗干擾技術方面，盡管基于取舍的體制從根本上說是自適應的，但典型的處理方法是在判斷出干擾的位置后，對各個變換域系數乘以權0或權1，即去除含干擾的變換域系數，保留不含干擾的變換域系數。因此，采用連續變換的權值并使用某種優化算法來調節權值，可以最大程度地改善系統性能。

由于變換域抗干擾方法具有很多優點，因此被認為是一種極具潛力的抗干擾策略，在時域很復雜的濾波過程中可以通過頻域簡單的相乘來完成，而且時域無法實現的理想濾波器傳遞函數，如矩形濾波器等，也可以很方便地在頻域實現。在擴頻通信領域，變換域處理技術可以有效地抑制干擾并改善系統性能。

1.2 FFT重疊變換干擾抑制算法

快速傅立葉變換（FFT）方法有：時間抽選基2FFT算法（庫里－圖基算法）、頻率抽選基2FFT算法。

時間抽選基2FFT算法（庫里－圖基算法）：

設N＝2M，M為正整數，把離散時間序列按時間進行奇偶分解

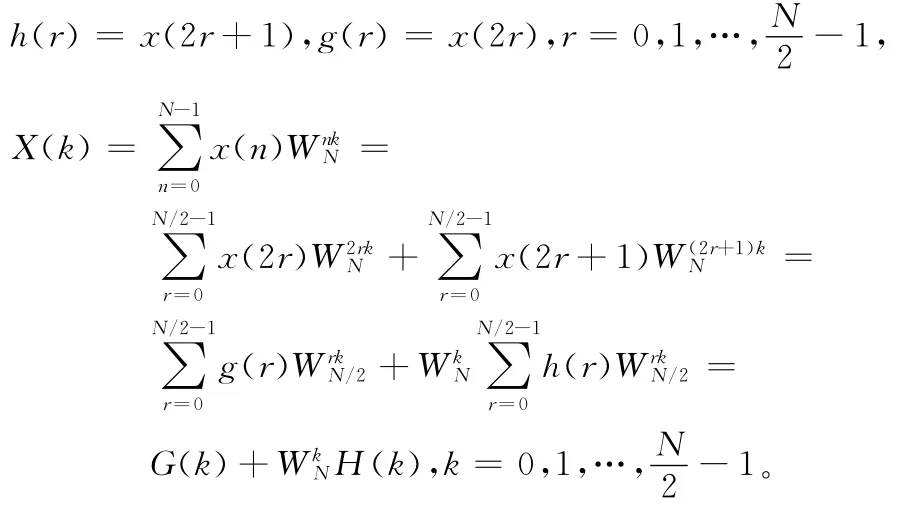
由上式可求出N/2個點的離散傅立葉變換。

后N/2個點的離散傅立葉變換為

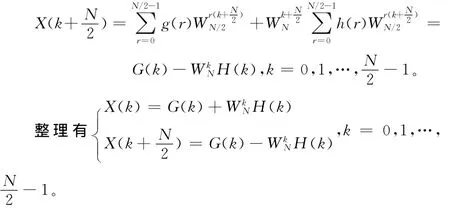
信號流圖如下：

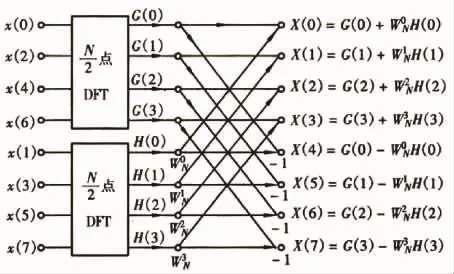
對G（k）和H（k）采用上述同樣的奇偶分解方式，可分別得

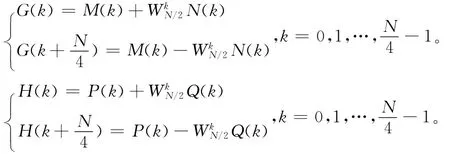
對M（k），N（k），P（k）和Q（k）均采用上述同樣的奇偶分解方式，可分別得N/8，N/16個點等等的離散傅立葉變換，依次類推，最后到2個點的離散傅立葉變換。

最后兩點的離散傅立葉變換

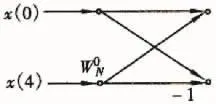
FFT具有M級、N/2個碟形運算。

頻率抽選基2FFT算法原理與時間抽選基2FFT算法原理相似，不同之處在于它是把輸出序列X（k）按其順序的奇偶分解為越來越短的序列。

FFT重疊變換干擾抑制算法的原理是窄帶干擾相對于擴頻信號能量集中在很窄的頻帶內，在頻域上就表現為很窄的尖峰，所以可先將混合信號變換到頻域，檢測出干擾的頻譜位置，將這些譜線去掉或進行衰減，最后反變換還原成時域信號進行解擴。［4］其原理框圖如圖2所示。

FFT重疊變換干擾抑制算法不需要自適應算法，且其處理速度遠遠超過時域濾波的算法。

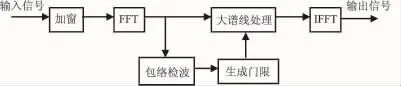
圖2 頻域陷波技術實現框圖

FFT重疊變換干擾抑制技術實現的數學模型如圖3所示。

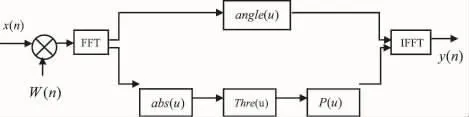
圖3 頻域陷波技術實現的數學模型

圖3中，W（n）是窗函數，abs（u）和angle（u）兩個函數分別求離散傅里葉變換后幅度和角度（相位）值，Thre（u）函數確定譜線的門限值，p（u）函數是對譜線進行處理。

2 抗干擾技術仿真與分析

仿真結果的各個波形圖如圖4所示。

由圖4（a）和4（b）可以看出，窄帶干擾基本被抑制了，圖4（b）已經可以比較清晰地看到信號的相位翻轉情況，但是由于噪聲存在（干擾抑制算法無法抑制噪聲影響），干擾抑制后的信號波形還有一定的起伏；圖4（c）是1/4重疊復用頻域陷波模塊各支路抗窄帶干擾后的波形及4路對齊疊加之后的信號波形，該波形圖橫坐標單位為“s”，縱坐標單位是“V”。由圖可見其幀信號兩端的衰減在對齊合并之后消失了；圖4（d）為含窄帶干擾信號經過重疊變換頻域陷波之后的信號頻譜圖。頻域陷波算法進行了加窗處理和1/4重疊變換，該措施使干擾的頻譜泄露大為降低，也使信號的損傷大為減少，這些因素促成了該算法良好的抗窄帶干擾性能。

在變換域干擾抑制技術中，基于FFT的干擾抑制技術優點是能夠處理多個干擾，并且可以快速跟蹤干擾的變化。它在設計干擾抑制算法時更自由，能提供更大的動態范圍，抑制干擾的數目僅與FFT變換長度有關。通過合理選擇窗函數和抑制算法，陷波深度可以非常大。由于FFT對接收數據的每一個記錄進行變換，因此實時FFT算法有能力對變化的干擾環境快速自適應。

圖4 抗干擾技術仿真波形圖

3 結論

擴頻通信以其較強的抗干擾、抗衰落、抗多徑性能而成為第三代通信的核心技術。［5］將基于FFT的干擾抑制技術用于擴頻通信系統，可使干擾的頻譜泄露大大降低，減少信號的損傷，由此提高了信息傳輸的準確性、可靠性。

參考文獻：

［1］ 杜思深，唐書娟.抗干擾通信與電子攻擊的發展［J］.中國新通信，2009（15）：68－70.

［2］ 于江，王春嶺，沈劉平，等.擴頻通信技術原理及其應用［J］.中國無線電，2010（03）：44－47.

［3］ 程佩青.數字信號處理教程［M］.北京：清華大學出版社，2001.

［4］ 趙剛.擴頻通信系統實用仿真技術［M］.北京：國防工業出版社，2009.

［5］ 靳麗平，韓慧蓮.直接序列擴頻通信系統研究及仿真［J］.電子測試，2011（1）：78－72.

（責任編校：夏玉玲）

Research on Anti－Jamming Technology in Spread Spectrum Communication System

ZHANG Yin－pu，SUN Mao－song，DOU Gui－hua

（Department of information Engineering，Tangshan College，Tangshan 063000，China）

For interference of Gaussian white noise and narrowband in wireless channel，overlap conversion FFT frequency domain notch filter algorithms can be adopted to reduce or eliminate relevant interference.Simulation analysis can be conducted in upon it in spread spectrum communication system.Results show that the technology can greatly reduced the interference spectrum leak and the signal damage and it improves the accuracy and reliability of information transmission.

anti－jamming technology；overlap conversion FFT frequency domain notch filter algorithms；spread spectrum communication

book=17,ebook=17

TN914.42

A

1672－349X（2012）03－0097－03

2012－03－16；

：2012－03－29

張銀蒲（1978－），女，河北保定人，講師，碩士，主要從事信號處理、控制工程研究。