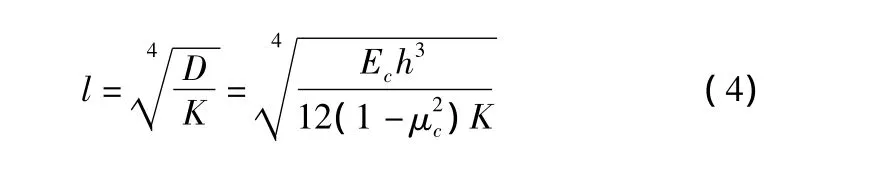溫克勒地基板的荷載應力分析

杜永新

(河北省遷安市交通運輸局質量監督站)

溫克勒地基板的荷載應力分析

杜永新

(河北省遷安市交通運輸局質量監督站)

從幾個方面介紹了溫克勒地基板的荷載應力分析。

溫克勒地基板;荷載應力;分析

溫克勒地基是以反應模量K表征的彈性地基。它假設地基上任一點的反力僅同該點的撓度成正比，而與其他點無關，即地基相當于由互不相聯系的彈簧組成，見圖1。這一假說首先由捷克工程師溫克勒(E.Winkler)提出，故稱溫克勒地基。地基反力q(x，y)與該點的撓度W(x，y)的關系為

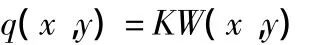
式中:K為地基反力模量，MPa/m。

威斯特卡德(H.M.S.Westergaard)采用這一地基假說，分析了圖2所示三種車輪荷載位置下板的撓度和彎矩，即①輪載作用于無限大板中央，分布于半徑為R的圓面積內。②輪載作用于受一直線邊限制的半元限大板的邊緣，分布于半圓內。③輪載作用于受兩條相互垂直的直線邊限制的大

板的角隅處，壓力分布圓面積的圓心距角隅點為。

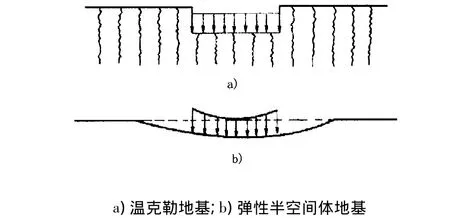
圖1 不同假設地基的表面變形圖

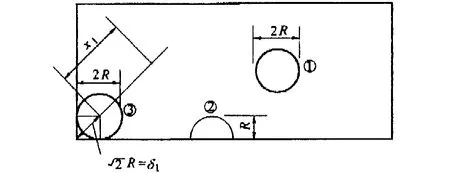
圖2 三種荷載位置

在解微分方程時，附加q=KW并引入邊界條件得出撓度w，再代入，最后得如圖2三種荷載情形的最大應力計算公式。

(1)荷載作用于板中(荷位①)，荷載中心處板底最大彎拉應力

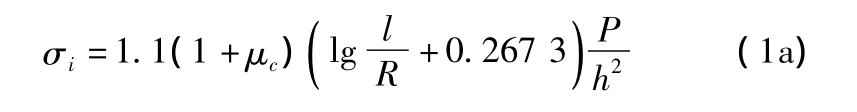
當荷載作用面積較小時，壓強p可能很大。這時，如果仍采用假設σz=0的薄板理論計算應力，會得出偏大的結果。威斯特卡德分析了薄板與厚板理論計算結果的差異，提出了一種把小半徑實際荷載面積放大成當量計算半徑b的近似方法。b和R的關系按下式確定

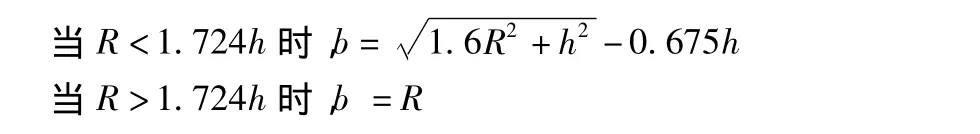
一般說來，當R≥0．5h時，按R和按b算得的應力值相差并不大，因而在這種情況下可不必按當量半徑計算應力，而當R＜0．5h時，則必須把R換算成b以后，才能應用式(1a)計算應力。

因此，式(1a)改寫為

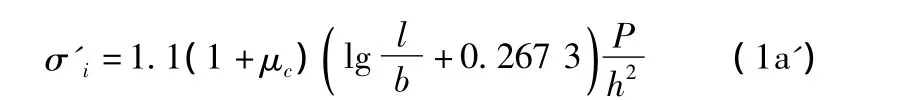
(2)荷載作用于板邊緣中部(荷位②)，荷位下板底的最大彎拉應力

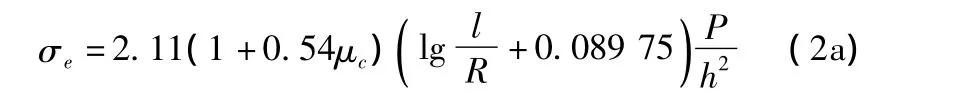
在試驗驗證上述公式時發現，當板處于同地基保持完全接觸的狀態時，計算結果同實測值相符。但在板邊緣由于板溫度翹曲變形或地基塑性變形而同地基脫空時，實測應力值要比式(2a)的計算結果偏高10%左右。為此，凱利(E.F.Kelley)根據試驗結果，提出了經驗修正公式

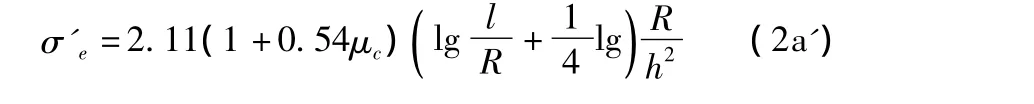
計算板邊應力σe時，當R＜0．5h時，也應將R改成b進行計算。

(3)荷載作用于板角隅(荷位③)，最大彎拉應力產生在板的表面離荷載圓中心為的分角線上。

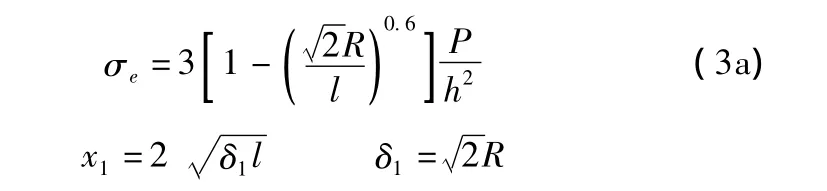
在溫度梯度和地基塑性變形的影響下，板角隅也會發生同地基相脫空的現象。試驗表明，板角隅上翹時，實測應力值要比按式(3a)算得的大30% ～50%左右。對此，凱利提出了經驗修正公式

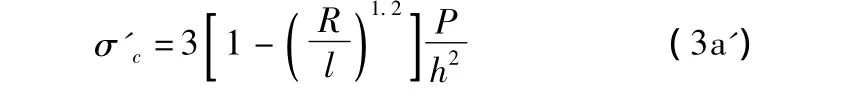
在以上諸式中，P為車輪荷載，為板的相對剛性半徑，即

U442

C

1008-3383(2012)05-0020-01

2011-12-19