相似度－遺傳神經網絡在儲層物性預測中的應用

董興朋

（中國地震局地震研究所，湖北武漢430071）

相似度－遺傳神經網絡在儲層物性預測中的應用

董興朋

（中國地震局地震研究所，湖北武漢430071）

傳統的測井解釋需要建立精確的數學模型，并常伴有嚴格的條件限制，因此很難得到真實反映儲層特性的結果。采用遺傳算法與BP神經網絡相結合，利用遺傳算法的全局尋優特點，優化神經網絡的連接權值和閥值，提高網絡的訓練精度和預測精度，避免了BP算法易陷入局部極小的缺點，提高運算速度。將相似度的概念引入到測井中，定義相似度在測井中的計算公式，提出相似度與遺傳神經網絡相結合的方法。實例研究表明，預測準確性較高，可以有效控制預測精度，避免因儲層差別大而造成的預測精度降低的現象。

地球物理測井；遺傳算法；相似度；神經網絡；儲層物性；預測

0 引 言

通過巖心取樣進行室內測試，獲取巖心的孔隙度精度很高，但取樣和測試的費用很高，致使獲取的儲層孔隙度數據有限，不能覆蓋整個工區［1］。常規測井解釋多通過經驗公式或簡化地質條件建立模型計算儲層參數。然而測井資料具有不確定性和非結構化的特點，過去采用的統計方法未能擺脫線性方程的束縛，使求得的物性參數很難與實驗數據建立良好的對應關系［2］。

BP神經網絡［3］的學習基于梯度下降法，因此存在收斂速度慢及網絡參數和計算參數難以確定等缺點［4］。遺傳算法（Genetic Algorithm，GA）是一種借鑒生物界自然選擇和自然遺傳機制的搜索算法，它能在復雜空間中尋找最優解，且有算法簡單、適用、魯棒性強等優點。基于以上2種算法各自的優缺點，可以將遺傳算法和BP神經網絡結合，提高網絡訓練精度。利用GA－BP神經網絡預測儲層物性參數，具有綜合利用多種測井參數，客觀反映輸入參數與儲層參數之間復雜規律和無需選擇測井解釋參數等特點。

本文將相似度的概念引入到測井中，提出了相似度與遺傳神經網絡相結合，并在MATLAB中進行預測，可以有效控制預測精度，避免因儲層差別大而造成的神經網絡預測精度降低的現象。

1 遺傳算法與神經網絡

1.1 標準BP算法

BP（Back Propagation）網絡是一種按誤差逆傳播算法訓練的多層前饋網絡，能學習和存儲大量的輸入－輸出模式映射關系，無需事前揭示描述這種映射關系的數學方程。它的學習規則是最速下降法，通過反向傳播不斷調整網絡的權值和閥值，使網絡的誤差平方和最小。理論證明，含有一個隱含層的BP網絡可以實現以任意精度近似任何連續非線性函數［5］。但在實際應用過程中，存在易陷入局部極小和收斂速度慢等缺點。針對這些缺點，已有人對此提出了改進方案，如修正學習率、增加動量項、引入陡度因子及改進神經元激勵函數等［3］。

1.2 遺傳算法原理

遺傳算法是借助生物的進化規律，使所要解決的問題從初始解一步步逼近最優解［6］。它是一種全局優化搜索算法，可以有效克服BP神經網絡易陷入局部最優的不足。遺傳算法一般包括選擇、交叉和變異3個基本操作。適應度函數（目標函數）被用來評價個體解的優劣程度，從而對個體進行選擇操作。控制GA處理效果的主要參數包括群體規模與交叉概率、變異概率。其流程見圖1。

圖1 遺傳算法流程圖

1.3 權值優化

用GA優化神經網絡可以使得神經網絡具有自進化、自適應能力，它主要包括網絡權值的進化、網絡拓撲結構的進化和學習規則的進化，而最主要的是用來優化網絡的權值［7］。遺傳算法優化神經網絡權值的一般步驟如下。

（1）確定BP神經網絡的拓撲結構和訓練樣本。

（2）對神經網絡權值編碼，遺傳控制參數初始化，產生含P個個體的初始種群（權值）。

（3）適應度函數的確定。一般以誤差函數的倒數作為染色體評價函數。誤差越大適應度值越小。

（4）計算每個個體的適應度，選擇若干適應度函數值大的個體直接進入小一代；適應度小的個體被淘汰。

（5）利用交叉、變異等遺傳算子對當前新一代群體進行新一輪迭代，直到訓練目標滿足終止條件為止。重復步驟（2）、（3）、（4）、（5），對新一代群體進行新一輪迭代，直到訓練目標滿足終止條件為止。

2 相似度在測井中的應用

2.1 儲層類型

影響儲層孔隙度的地質因素有埋藏深度、構造位置、沉積環境、巖性變化、成巖程度等。沉積環境對儲層物性的影響一直是定性說明，由于在不同的沉積環境中會形成不同的沉積序列，也就會有不同的砂地體積比值［8］。最常見的有3類：沖積扇沙礫巖儲層、河流砂體儲層和三角洲砂體儲層。在相同的儲層類型中，由于沉積環境相同，可以認為測井信息與儲層參數之間的非線性映射是相似的。

2.2 相似度在測井中的定義

在相同的沉積環境（即沖積扇沙礫巖儲層、河流砂體儲層和三角洲砂體儲層3類），取標準的儲層模型i，該模型指標特征值的向量μi＝（μi1，μi2，…，μik），其中，μi1，μi2，…，μik分別為儲層k種不同測井曲線值；取所要預測的儲層為樣本j，指標特征值向量為rj＝（rj1，rj2，…，rjk），k種不同的測井技術對儲層物性影響的權重分別為wj1，wj2，…，wjk則樣本j相對標準模型i的相似度為

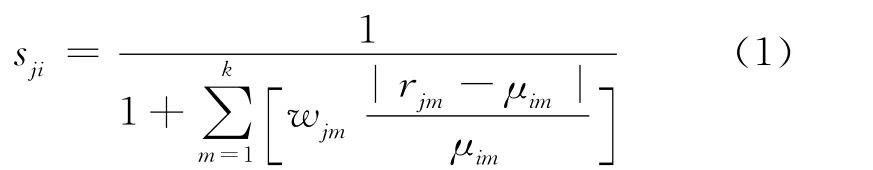
有了相似度的定義，在進行儲層相似度預測時就可以先計算所要預測儲層與已知模型的相似度。若相似程度很高，就可以直接用經過已知模型訓練的神經網絡對未知儲層的孔隙度進行預測。

3 GA－BP網絡模型及MATLAB實現

用神經網絡預測儲層物性參數，就是尋求測井信息與儲層物性參數之間的某種非線性映射。BP網絡是一種按誤差逆傳播算法訓練的多層前饋網絡，很好地解決了輸入和輸出之間的關系和復雜的非線性問題，為儲層參數的預測提供了一種有效的途徑［2］。

MATLAB中的神經網絡工具箱以神經網絡為基礎，利用MATLAB腳本語言構造出典型的神經網絡激活函數，使設計者對所選網絡的計算變成對激活函數的調用，為用戶提供了極大方便［2］。基于MATLAB的GA－BP網絡實現儲層物性預測的一般步驟如下。

（1）原始資料的預處理。巖心實驗數據及測井數據的預處理包括巖心數據和測井數據的深度歸位，使得巖心分析所得的物性參數和測井信息來源于同一深度。

（2）選取學習樣本。

（3）數據的歸一化處理。使用premnmx函數進行歸一化處理，使數據分布在［－1～1］之間。

（4）構建預測網絡模型。根據神經網絡的連續函數映射定理，具有3層（1個輸入層、1個隱含層和1個輸出層）的網絡結構，即可實現任意連續函數從輸入空間向輸出空間的映射［3］。本文采用3層的神經網絡結構，輸入神經元數為測井參數的個數，輸出神經元為1個（孔隙度或滲透率），隱含層節點數較難確定，節點數太多，網絡訓練時間長；節點太少，誤差精度又達不到要求。用學習樣本集訓練網絡，直到精度滿足要求為止，保存網絡，建立儲層參數預測網絡模型。

（5）應用上述建立的預測網絡模型預測未知儲層層段的物性參數。

4 孔隙度的預測

4.1 基于GA－BP神經網絡的孔隙度預測

以寧東5井延長組目的層段的7個樣本為訓練樣本作為神經網絡的輸入，巖心孔隙度作為訓練樣本輸出值，選取反映儲層孔隙度參數敏感的聲波（AC）、密度（DEN）、中子測井（CNL）和自然伽馬（GR）等4種測井曲線作為輸入元，隱含層的神經元數為25，輸出層神經元為1，建立GA－BP神經網絡模型（樣本訓練數據見表1）。

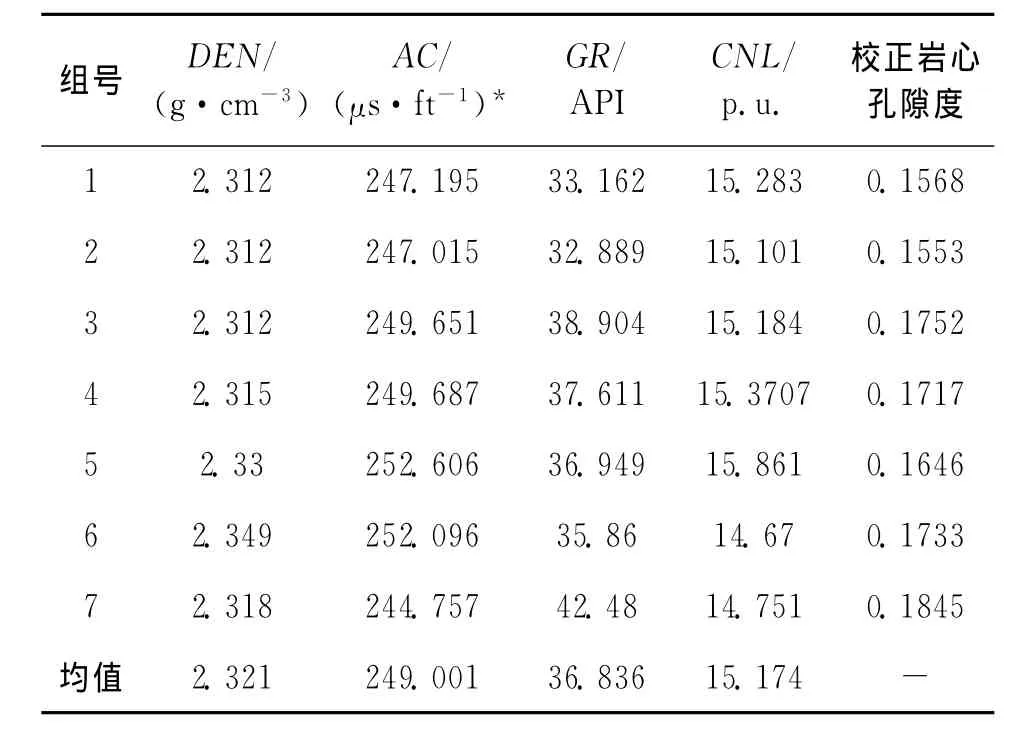
表1 樣本訓練數據

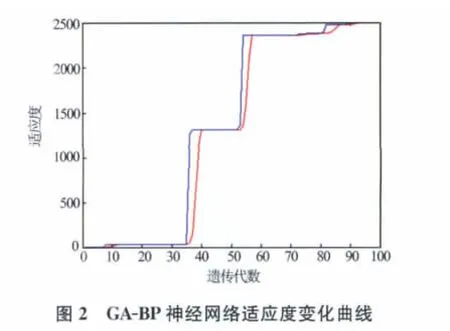
GA－BP神經網絡染色體編碼采用實數編碼，適應度函數為誤差平方和的倒數。種群規模為50，遺傳代數為100，網絡最大訓練次數為1 000，訓練誤差精度為0.000 1。用訓練樣本訓練網絡，經過100代遺傳操作，得到遺傳算法優化的BP網絡初始權值和閥值，適應度函數值為2 300（見圖2）；再用共軛梯度BP算法訓練網絡，經過35次迭代，均方差誤差達到訓練誤差精度0.000 1（見圖3）。

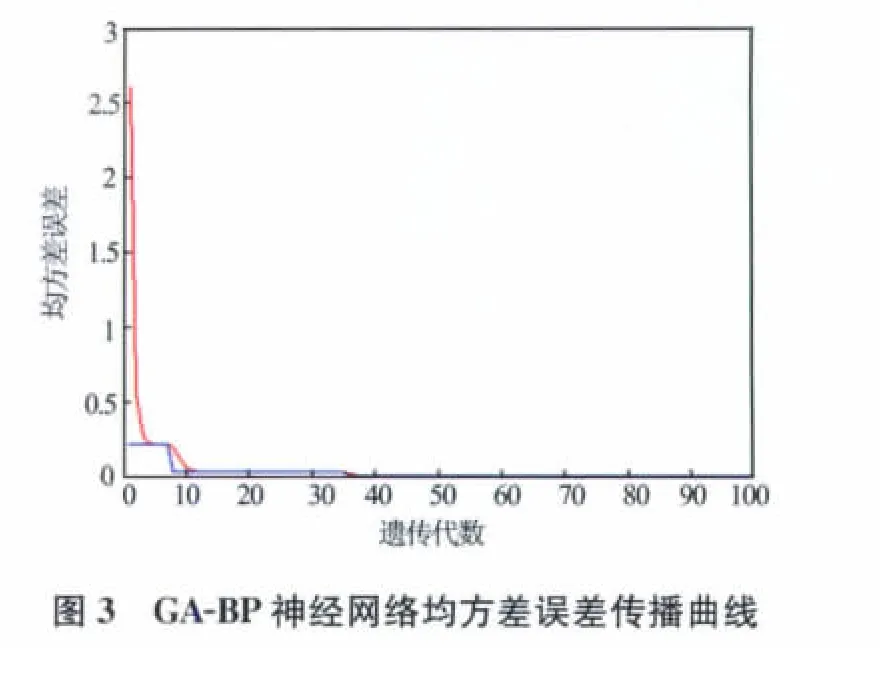
取3組數據作為測試樣本進行預測。取訓練樣本與測井輸入曲線的平均值作為標準儲層模型的指標特征值，根據式（1），取權重均為0.25，計算3組測試樣本的相似度。預測結果見表2，誤差隨相似度變化曲線見圖4。

由表2和圖4知，當所預測樣本與訓練樣本的相似度高時，預測精度很高；反之，預測精度不高，存在較大的誤差。隨著相似度的增大，GA－BP神經網絡預測的誤差逐漸減小。因此，在孔隙度預測之前，須先計算預測樣本的相似度，以判斷是否適合，這樣，可以有效控制預測精度，避免因儲層差別很大而造成的神經網絡預測精度降低的現象。

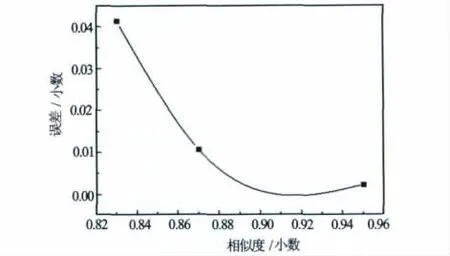
圖4 誤差隨相似度的變化曲線

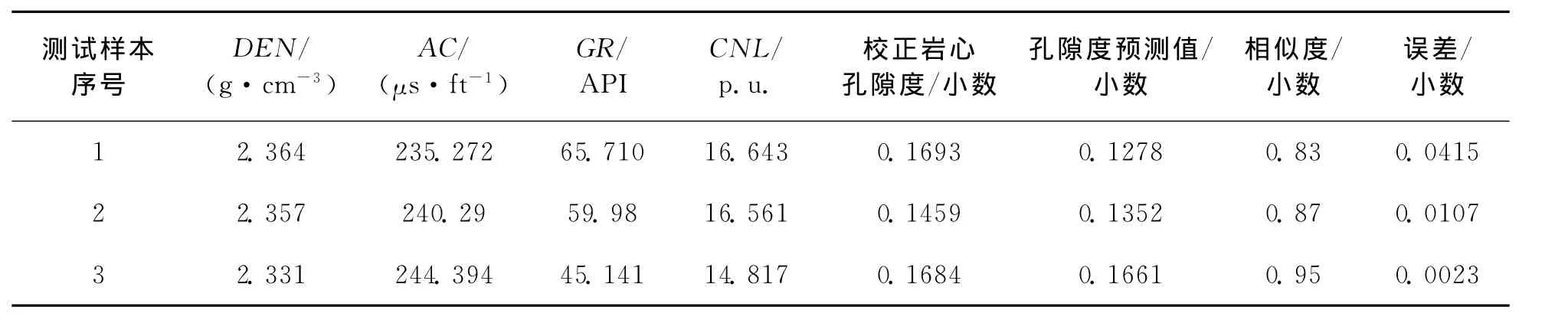
表2 GA－BP神經網絡孔隙度預測數據表

4.2 GA－BP算法與標準BP算法預測結果對比

同樣，以表2中3組樣本為測試樣本，采用標準BP算法對樣本孔隙度值進行預測（預測結果見表3、圖5）。由表3可知，采用標準BP算法得到的預測值的誤差高于采用GA－BP算法的誤差。樣本1由于相似度較低，2種算法得到的誤差都較高；樣本2和3采用GA－BP算法得到的預測值的誤差遠小于標準BP算法，證明了GA－BP算法相對于傳統的標準BP算法的優勢；圖5中，GA－BP算法和標準BP算法預測的誤差都隨著相似度的增加而減小，證明了將相似度引入到儲層孔隙度預測中的必要性。

表3 GA－BP算法同標準BP算法預測結果對比

5 滲透率的預測

巖石滲透率受孔隙度、粒度、分選、磨圓、礦物組成和黏土分布等諸多因素直接或間接影響［2］。選取孔隙度以及自然伽馬（GR）、電阻率（Rt）、聲波（AC）、密度（DEN）、中子測井（CNL）等作為網絡的輸入，巖心滲透率為網絡的輸出。以寧東5井為例，選取7個樣本為訓練樣本作為神經網絡的輸入，預測模型采用3層的神經網絡，其中輸入神經元6個，隱含層神經元25個，輸出神經元1個。GA－BP神經網絡設置與上文中孔隙度預測設置相同，求相似度時，自然伽馬（GR）、電阻率（Rt）、聲波（AC）、密度（DEN）、中子測井（CNL）權重均取0.15，孔隙度權重取0.25。訓練樣本數據和預測結果見表4和表5。可以看出，同孔隙度預測一樣，隨相似度的減小，GA－BP神經網絡預測精度降低。

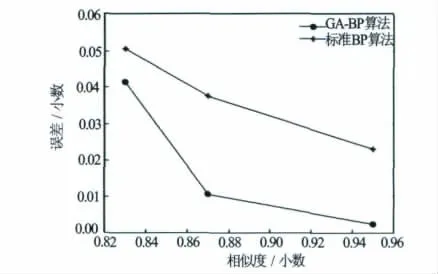
圖5 GA－BP算法同標準BP算法預測結果對比圖

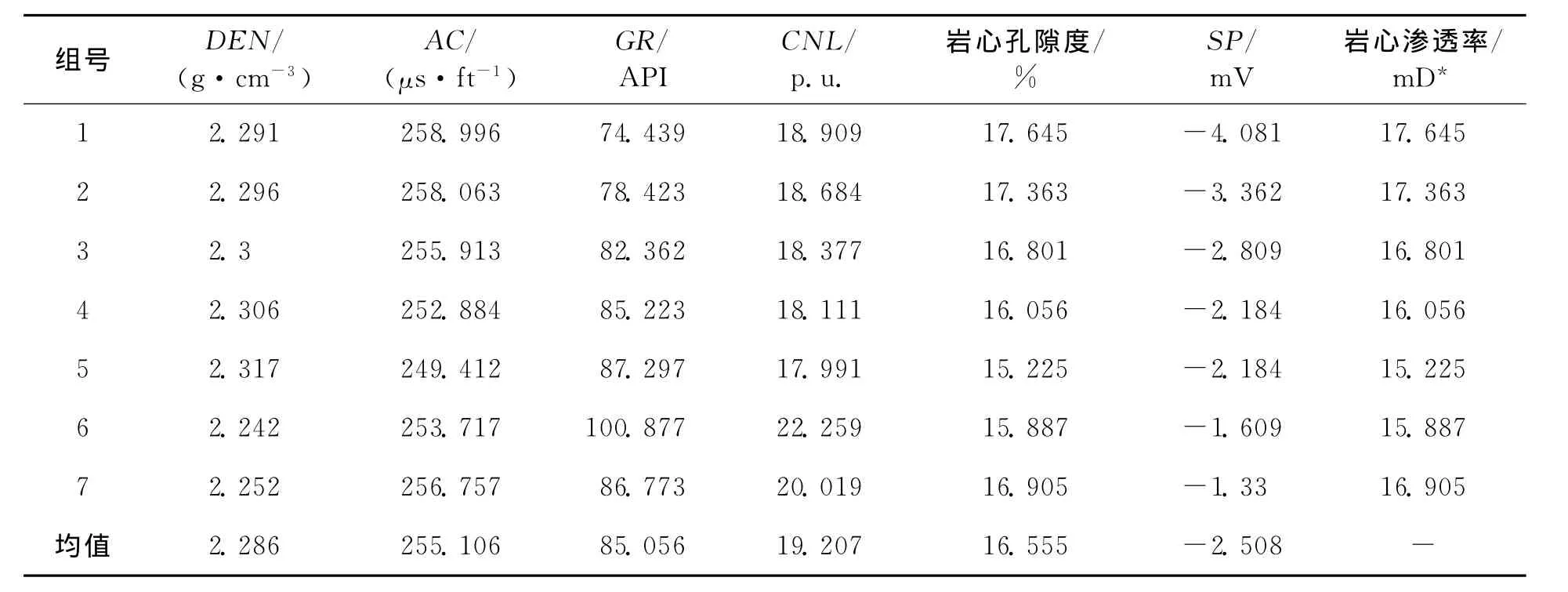
表4 訓練樣本數據

表5 GA－BP神經網絡滲透率預測數據表

6 結 論

（1）利用BP神經網絡可以建立起測井響應和儲層物性參數之間的非線性映射關系，將遺傳算法與BP神經網絡相結合，優化了神經網絡的權值和閥值，避免了標準BP算法易陷入局部極小的缺點，為儲層物性預測提供了一條很好的途徑。

（2）通過MATLAB工具箱庫函數的調用就可以很容易實現GA－BP神經網絡的建模，免去了繁雜的編程，提高了研究效率。

（3）將相似度的概念引入到測井儲層物性預測中。實例研究表明，相似度越高，GA－BP神經網絡預測誤差越小。因此，在儲層物性參數預測之前，須先計算預測樣本的相似度，以判斷是否適合，這樣可以有效地控制預測精度，避免因儲層差別大而造成的神經網絡預測精度降低的現象。

［1］ 連承波，李漢林，渠芳，等.基于測井資料的BP神經網絡模型在孔隙度定量預測中的應用［J］.天然氣地球科學，2006，17（3）：382－384.

［2］ 陳蓉，王峰.基于MATLAB的BP神經網絡在儲層物性預測中的應用［J］.測井技術，2009，33（1）：75－78.

［3］ 陳鋼花，董維武.遺傳神經網絡在煤質測井評價中的應用［J］.測井技術，2011，35（2）：171－175.

［4］ 林香，姜青山，熊騰科.一種基于遺傳BP神經網絡的預測模型［J］.計算機研究與發展，2006，43（suppl.）：338－343.

［5］ 謝立春.BP神經網絡算法的改進及收斂性分析［J］.計算技術與自動化，2007，26（3）：52－56.

［6］ 趙軍，祁興中，宋帆，等.遺傳算法在測井識別凝析氣藏中的應用［J］.測井技術，2006，30（4）：313－316.

［7］ 洪露，馬長山，謝宗安.基于遺傳算法的神經網絡權值優化［J］.貴州工業大學學報：自然科學版，2003，32（6）：48－51.

［8］ 王朋巖.用神經網絡預測儲層的孔隙度［J］.大慶石油學院學報，2003，27（2）：5－7.

Application of Similarity－Genetic Neural Network to Reservoir Parameters Prediction

DONG Xingpeng
（Institute of Seismology，China Earthquake Administration，Wuhan，Hubei 430071，China）

Due to the anisotropy of reservoir，using the linear method it is difficult to get actual reservoir characteristics.On the basis of a combine of genetic algorithm and BP neural network，the global random hunting function of the genetic algorithm is used to optimize neural network connection weights and threshold，which enhances the network tranining precision and parameters prediction accuracy，and as well，increases computing speed by avoiding its disadvantages that standard BP algorithm is apt to trap in local minimal solution.At the same time，we define the similarity in well logging and its calculation formula，and propose a predicting method to combine similarity and Genetic Neural Network.Compared with real samples，the predictive accuracy is higher and effectively controlled，enhance the neural network prediction accuracy.

geophysics logging，genetic algorithm，similarity，neural network，reservoir physical property，prediction

P631

A

2011－12－05 本文編輯 李總南）

1004－1338（2012）03－0267－05

董興朋，男，1988年生，在讀研究生，研究方向為固體地球物理。