規劃層面的危險品運輸路徑優化模型

馮樹民，殷國強

(哈爾濱工業大學交通科學與工程學院，150090哈爾濱)

危險品運輸路徑優化不但能夠減小危險品運輸事故發生的可能性，同時還能降低事故后果，對城市危險品運輸的安全保障有較為深遠的意義.在危險品運輸路徑優化問題上，國內外科研工作者進行了大量研究.Miaou等［1］利用最短路線算法求解運輸成本、事故概率和暴露人口約束的最佳路線;Erkut等［2－3］通過研究多種危險品運輸風險評價模型，選用6個標準，對選線問題“最優路徑”的相似相異性進行系統分析;Zografos等［4］提出了在考慮時間參數情況下的最小化運輸風險和最低運輸成本的混合整數規劃;吳宗之等［5－8］研究了危險品運輸目標體系，分別以運輸風險、事故總概率、暴露人口數等為目標分別建立了危險品運輸路徑優化模型;秦軍昌等［9］考慮路徑優化中的天氣因素，提出了危險品運輸選線的魯棒優化模型;魏航等［10-11］將危險品運輸風險分為人口風險、環境風險和財產風險3部分，并考慮了危險品運輸過程人口風險的時間屬性以及區域風險差異和個體風險差異，構建了運輸風險平衡性模型.

危險品運輸路徑優化選線指標很多，在不同研究階段有些選線指標獲取存在困難，且各指標之間容易發生沖突，并且以往的優化模型多數偏重理論分析，實用性較差.

1 規劃層面的危險品運輸路徑優化指標體系

危險品運輸路徑優化指標大致包括影響人員風險指標、道路特征指標、環境風險指標、成本指標等.其中影響人員風險指標包括影響人數、社會風險、避災減災風險、感知風險和條件風險等;道路特征指標包括路線長度、行駛時間、道路事故率等;環境風險指標主要考慮揮發性危險品事故發生后的揮發特性;成本指標主要指運輸成本.

在危險品運輸過程中影響因素較多，需要考慮的指標也很多，并且眾多的路徑優化標準之間容易發生沖突，如成本最小的運輸路線的潛在運輸風險通常較大，而較小的運輸風險路線的運輸成本可能會相對較高.因此在進行危險品運輸路徑優化時，應綜合考慮各方面要求.

在確定危險品運輸路徑優化指標時，考慮到主要是用于比較不同運輸路線之間的優劣，因此不考慮車輛、駕駛員等共同的因素，只考慮能反映不同路徑優劣的指標.這些指標應能體現出危險品運輸過程主要相關方的利益，同時確定的指標應可以量化.

危險品運輸過程主要涉及兩個部門的利益，政府部門主要關注危險品運輸的風險大小，運輸企業則主要關注經濟成本問題.如果路線的選擇只是滿足政府對于風險控制的需求，而忽視了企業運輸的成本要求，勢必導致選線脫離實際，因此在路徑優化過程中必須協調好二者關系，使危險品運輸選線能夠達到政府與企業間的雙贏.因此將危險品道路運輸路徑優化指標分為兩大類:運輸風險和運輸成本.

考慮到危險品運輸事故屬于低概率重后果事件，所以在危險品運輸路徑優化中必須將運輸風險指放在第一位.對于運輸風險指標，以往研究都考慮了路段事故率以及沿線暴露人口數等因素.在規劃路網層面上，事故率無法得到，從可實施以及可量化角度考慮，選取規劃道路的實際道路情況(道路等級、橫斷面形式)作為影響將來道路事故率的主要指標;暴露人口與用地性質密切相關，故選取道路沿線用地性質指標作為評估事故后果的主要指標;考慮到應急能力對于危險品事故的重要性，將事故應急能力也作為運輸風險的影響因素.

對于運輸成本指標，結合交通領域的相關理論，以路段的時間阻抗為依據，主要考慮道路長度、設計車速、路段飽和度等影響因素.

綜上，得到危險品運輸路徑優化指標體系見圖1.

圖1 危險品運輸路徑優化指標體系

2 危險品運輸路徑優化指標量化

2.1 運輸風險指標量化

危險品運輸風險通常定義為危險品運輸過程事故率與潛在損失后果的乘積.事故發生概率往往受時段、天氣狀況、道路類型、車輛類型、裝載形式和路況等方面的影響，而事故后果嚴重度與影響人數、財產損失以及氣象條件和風向概率等有關.

以往研究都是在現有道路基礎上進行的，結合以往數據得到相應危險品運輸路段事故率，而在規劃路網上路段的事故率無法得到，同時與事故后果相關的數據也無法得知.

在城市規劃道路網上，考慮道路的特性以及道路沿線的用地性質，提出路段風險計算如下:

式中:R為路段風險值;A為路段的安全系數;ρi為第i種用地所對應的人口密度;si為路段沿線的第i種用地的面積.

對于一些具有揮發性的危險品運輸泄漏事故和一些造成了重大人員傷亡的事故，救援工作刻不容緩.事故發生路段的應急響應能力，對于潛在的運輸風險計算來說是一個不可忽視的因素，因此將事故應急能力作為補償因子，加入到危險品運輸的風險值計算當中，即

式中:R'為修正后的危險品運輸路段風險;E為路段發生事故時的應急響應能力;E*為有效的應急響應能力下限值;λ為調整參數，表示應急能力對事故后果的影響程度.

由此得到危險品運輸路徑的風險值為

式中:RL為危險品運輸路徑L的運輸風險;Aj為路段j的安全系數;Ej為路段j的應急響應時間.

2.2 運輸成本指標量化

從運輸企業角度看，危險品運輸不同于一般貨物，運輸成本比一般貨物要高.綜合考慮危險品運輸的全過程，將運輸成本用行駛時間來近似描述.一般來說，路段所需行駛時間并不是常數，而是與路段的交通有關，行駛時間的一般表達式為

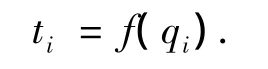
式中:ti為路段i的實際行駛時間;qi為路段i的交通量.

對于行駛時間函數的研究，應用最廣泛的是由美國公路局開發的函數，稱為BPR函數.

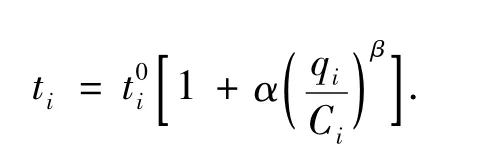
式中:t0i為路段i的自由流行駛時間;Ci為路段i的交通容量;α，β為參數，通常α=0.15，β=4.

由于研究從規劃路網的層面出發，故各條路段的飽和度(q/C)為規劃路網需求預測下的飽和度，并非實際的飽和度.

由此得到危險品運輸路徑的運輸成本為

式中TL為危險品運輸路徑L的運輸成本.

3 指標量化實例分析

圖2為萍鄉市2020年規劃的城市主要貨物運輸通道，危險品運輸通道的選取都是基于干道考慮的，對于支路的運輸并沒有考慮在內.該規劃路網共涉及21個節點，37條路段，這些路段均由主干道、快速路以及高速路改建段構成.大圓點表示危險品的產生吸引的區域，十字表示醫療衛生部門.

圖2 萍鄉市貨物運輸通道

路段安全系數A由路段長度、路面寬度以及道路橫斷面形式決定，考慮危險品運輸屬于特殊貨物運輸，運輸通道的選取只考慮主要干道.文獻［12］發現，當路面寬度＞30 m時，路段的事故率變化并不明顯，在研究對象上只是根據道路等級以及橫斷面形式來研究，橫斷面形式只考慮有無中央分隔帶.確定道路安全系數見表1.

表1 道路安全系數評定標準

道路沿線暴露人口密度由道路沿線的規劃用地性質來計量，用地面積按照危險品運輸事故影響范圍半徑800 m和路段長度計算.各類用地所對應的暴露人口密度考慮采用各類性質的用地所占吸引權重比來確定，結合以往研究成果［13］，確定各類用地的吸引權重比見表2.結合萍鄉當地情況取道路沿線居住用地人口密度為500人/km2，則其他各類用地的人口密度就可以推算出來.

表2 各類用地的吸引權重

統計各路段沿線的用地性質，結合道路等級以及橫斷面形式即可得到各個路段初步的風險值，應用風險校正模型，加入應急能力作為校正因子，取有效響應時間為5 min，即E*=5 min，取λ=0.25.計算得到各個路段校正后的風險R值，見圖3.

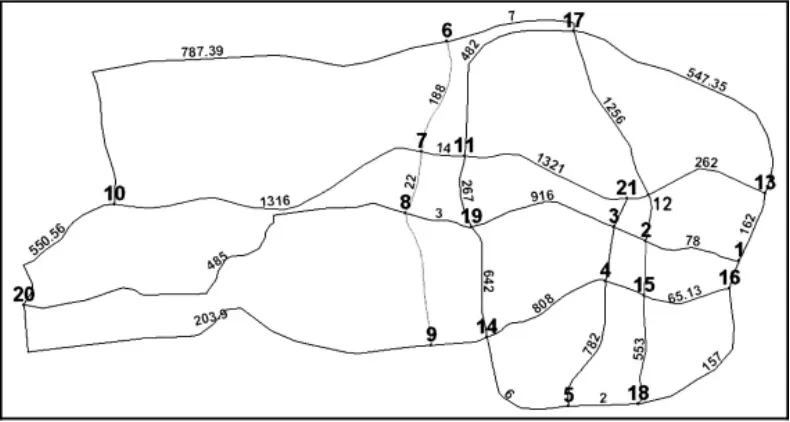
圖3 路段危險品運輸風險

對于成本指標的量化，需要統計各個路段的長度，設計車速以及預測的飽和度.在成本計算中，對于設計車速，高速公路按照120 km/h，快速路按照90 km/h，主干道按照70 km/h計算.路段飽和度按照需求預測結果給出.路段成本計算結果見圖4.

圖4 路段危險品運輸成本

4 危險品運輸路徑優化模型

以運輸風險最小和運輸成本最小為目標，建立危險品運輸路徑雙目標優化模型

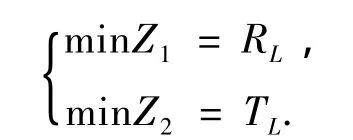
對于雙目標路徑優化選擇問題，一般情形下，選線不太可能同時使兩個目標達到最優，所以理論上講并不存在絕對最優路徑.

由于運輸風險與運輸成本之間存在沖突，準確評估目標間的沖突問題非常困難，通常做法是采用權重法將多目標問題轉化為單目標問題，形成單一的線性評估函數.也可構建多個沖突指標，生成一組Pareto優化路線，由決策者選擇最佳路徑［14］.還可以采用灰色關聯度投影法求取最優路徑［15］.

5 結論

1)規劃層面的危險品運輸路徑優化建立在規劃路網上，不同于以往的路徑優化，提出適合規劃層面的危險品運輸路徑優化指標體系.

2)從可量化、可實施角度選取以規劃路網的性質以及道路沿線的用地性質來量化路段運輸的風險，同時將醫療衛生點到路段的最快響應時間作為應急能力，并將應急能力作為補償因子加入到風險計算當中，改進了傳統風險模型.以車輛行走時間BPR阻抗函數作為路段運輸成本.

3)以萍鄉市總體規劃為背景，根據規劃道路的性質以及沿線用地性質，對危險品運輸的各路段運輸風險和運輸成本進行量化，給出具體計算過程.

4)以運輸風險最小和運輸成本最小為目標，建立雙目標危險品運輸路徑優化模型，探討了模型的求解方法.

［1］MIAOU S P，CHIN S M.Computing k-shortest path for spent nuclear fuel highway transportation［J］.European Journal of Operational Research，1991，53:64 －80.

［2］ ERKUT E，INGOLFSSON A.Catastrophe avoidance models for hazardous materials route planning［J］.Transportation Science，2000，34(2):165 -179.

［3］ERKUT E，INGOLFSSON A.Transport risk models for hazardous materials:revisited［J］.Operations Research Letters，2005，33(1):81 －89.

［4］ZOGRAFOS K G，ANDROUTSOPOULOS K N.A heuristic algorithm for solving hazardous materials distribution problems［J］.European Journal of Operational Research，2004，152(2):507－519.

［5］師立晨，魏利軍，吳宗之.危險品道路運輸多目標路徑優化方法研究［J］.中國安全生產科學技術，2006，10:60－63.

［6］WU Zongzhi，DUO Yingquan，LIU Mao，et al.A study on the methods of risk assessment of hazardous materials during road-transportation［J］.Journal of Basic Science and Engineering，2004，12:36 －44.

［7］任常興，吳宗之.危險品道路運輸選線問題分析［J］.安全與環境學報，2006，6(2):84－88.

［8］任常興，吳宗之，李晉.基于風險分析的危險品道路運輸多目標Pareto最優選線［J］.中國安全生產科學技術，2008(2):10-13.

［9］秦軍昌，張金梁，王刊良.危險品運輸線路問題的魯棒優化模型［J］.統計與決策，2009(20):25－26.

［10］WEI Hang，LI Jun.Analysis of population risk in hazardous material transportation as time varies［J］.China Safety Science Journal，2004，14(10):95 －98.

［11］WEI Hang，LI Jun，WANG Hao.Analysis of total risk of hazardous material during transportation［J］.China Safety Science Journal，2004，15(12):97 -101.

［12］景天然.城市道路條件與交通事故率的關系［J］.同濟大學學報，1992(3):35－40.

［13］韓春燕，殷國強，馮樹民.贛州市道路網規劃研究［J］.公路，2010(6):163 -167.

［14］魏航，蒲云，李軍.一種求解雙目標最短路的方法［J］.系統工程，2005(7):113-117.

［15］呂鋒，崔曉輝.多目標決策灰色關聯投影法及其應用［J］.系統工程理論與實踐，2002(1):103-107.