純電動汽車動力總成懸置系統的優化*

徐中明，李 曉，劉和平

(重慶大學，1.機械傳動國家重點實驗室;2.機械工程學院;3.輸配電裝備及系統安全與新技術國家重點實驗室，重慶 400030)

前言

動力總成懸置是指利用較柔軟的連接元件將動力總成與車架相連接，從而衰減二者之間的振動傳遞，起到隔振、支承和限位的作用。動力總成懸置系統的隔振性能直接影響到整車的NVH性能。目前，國內外對發動機動力總成懸置系統的研究已較深入，論文成果也較多。常采用的研究方法主要有轉矩軸解耦［1］和能量解耦［2］等。文獻［3］～ 文獻［5］中在這方面做了比較深入的研究，分析了懸置參數對懸置系統的固有頻率、解耦魯棒性和總成質心位移與支承處動反力幅頻特性的影響。

對于純電動汽車動力總成懸置系統的研究工作主要集中在動力總成固有特性的分析和優化匹配上，沒有結合電機驅動的特點進行起步、制動和其它工況的瞬態分析［6］。電動機與發動機的特性有很大不同，傳統的分析方法可以借鑒，但在研究純電動汽車動力總成懸置系統的隔振問題時必須考慮電動機的特點。

本文中采用ADAMS軟件對電動汽車的動力總成懸置系統進行建模。根據電動汽車在實際運行中出現的振動問題，結合電機的驅動特性對電動汽車的加速和制動兩種工況進行仿真分析，并以能量解耦為目標對其進行優化，以期為解決電動汽車動力總成懸置系統的振動問題提供一種有效途徑。

1 動力總成懸置系統動力學建模

該動力總成由三相異步感應電機、減速器和差速器組成，其中差速器集成在減速器內。動力總成和懸置元件一起組成動力總成的懸置系統，其固有頻率通常在30Hz以下，比動力總成自身的自由模態頻率低得多。因此在研究動力總成懸置系統的隔振特性時將動力總成簡化為6自由度的剛體模型，將橡膠懸置元件簡化為3向正交的彈簧阻尼模型。電動車動力總成如圖1所示。其中①②③分別表示3個橡膠懸置元件的安裝位置。

坐標系原點取在該動力總成的質心處，X軸平行于水平面并指向汽車前進方向，Z軸垂直向上，Y軸平行于電機轉子軸線，方向根據右手定則確定。定義動力總成的振動分別為在X、Y、Z軸上的平動x、y、z和繞 X、Y、Z 的轉動 α、β、γ，則動力總成的廣義坐標可表示為

根據振動理論建立動力總成懸置系統的振動微分方程為

式中:［M］為質量矩陣;［C］為阻尼矩陣;［K］為剛度矩陣;{Q(t)}為廣義坐標向量;{F(t)}為廣義力向量。

在求解動力總成懸置系統的固有頻率時不考慮阻尼的影響，則其無阻尼自由振動微分方程為

2 懸置系統固有特性和耦合特性分析

固有頻率是動力總成懸置系統的重要特性之一，通過分析懸置系統的固有頻率可以判斷其是否滿足懸置系統的隔振性能要求。懸置系統的固有頻率可通過式(3)變換后得出，即

通常動力總成懸置系統6個自由度方向上的振動是相互耦合的，一個方向上的激勵會引起多個方向上的振動。這一般會使系統的振幅加大，振動頻帶加寬。

利用ADAMS/Vibration模塊計算該動力總成懸置系統的各階固有頻率和模態能量解耦率，其結果如表1所示。

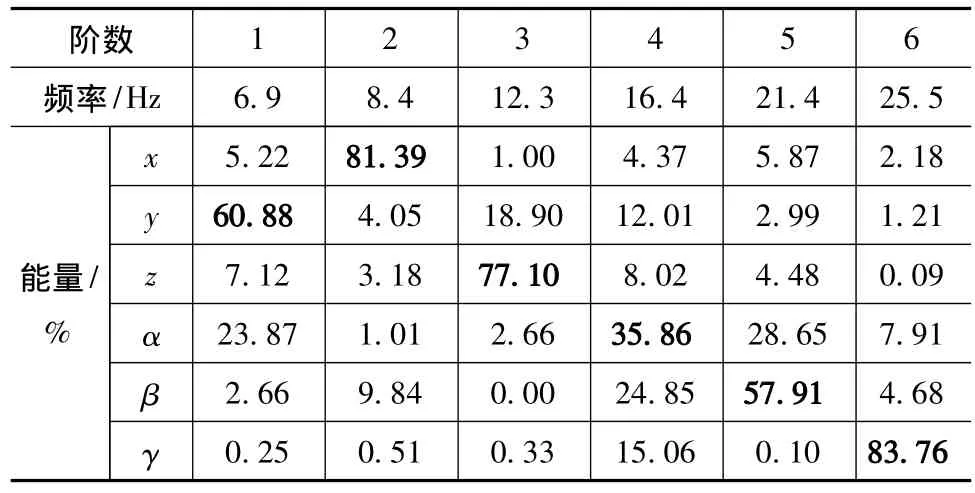
表1 動力總成懸置系統各階固有頻率和振動能量

電動汽車車身的頻率在2Hz左右，輪胎頻率在10Hz左右，由表1可知，該動力總成懸置系統的固有頻率在6～30Hz之間，垂向頻率12.3Hz。從頻率來看和固有頻率不很接近。從其能量分布百分比上看，各方向的解耦率都不高，最高的解耦率(第2階的x向和第6階的γ向)也只有81.39%和83.76%，最低的解耦率僅35.86%，說明該懸置系統的耦合非常嚴重，設計很不合理。

3 動力總成懸置系統瞬態響應分析

電動機與發動機的動力特性有很大不同。電動機在轉速為零時也能輸出很大的轉矩，且響應速度很快，能夠在極短時間里使輸出轉矩發生很大變化。運行中發現電動汽車在急加速和緊急制動工況下其懸置系統的振動非常嚴重。

利用ADAMS/View對電動汽車的加速和減速工況進行仿真分析。在10s的時間里同時計算電動汽車在加速和減速兩種工況下的瞬態響應。其中0～5s這一時間段電動汽車以最大驅動力矩原地起步加速，5～10s這一時間段電動汽車通過控制器以能量回饋的方式進行制動。電機的最大驅動力矩為120N·m，制動力矩為80N·m，電機響應時間取1ms，同時考慮動力總成所受重力和慣性力的影響。慣性力通過樣車整車結構參數和驅動(制動)條件計算加(減)速度來確定。仿真中忽略電機轉矩波動的影響，轉矩的加載曲線如圖2所示，動力總成慣性力的加載曲線如圖3所示。

仿真結果如圖4～圖8所示。

由圖4～圖8可見，在0～2s的時間段，即電動汽車在驅動時動力總成懸置系統主要的瞬態響應階段，曲線振動較大，之后振動趨于穩定。制動時系統從穩態階段進入瞬態階段，在系統主要瞬態階段的5～7s，振動也較大，之后又逐漸趨于穩定。這個過程符合實際中汽車在起步和制動時懸置系統從穩態進入瞬態，之后又恢復到穩態的狀況，說明用10s時間同時仿真計算電動汽車的起步和制動過程是可行的。

從圖4～圖6可以看出，驅動工況時動力總成懸置系統的質心Z向位移較大，幅值接近3.5mm，質心Z向加速度也較大;制動時質心Y向角加速度較大。這主要是由于電動機動力總成自身激勵的特點使動力總成懸置系統在Z向的垂直振動和繞Y軸的俯仰振動比較嚴重，另外路面激勵也是一部分原因。從能量耦合的程度也可看出，第3階模態的Z向能量解耦率只有77.10%，第5階模態的β向能量解耦率只有57.91%，耦合相當嚴重。

由圖7和圖8可見，橡膠懸置元件的Z向受力和變形比較大。其中懸置2的值最大，最大力為876N，最大為位移4.9mm。制動時力和位移的變化范圍也較大。這樣不僅會產生運動干涉，還容易使橡膠元件發生疲勞破壞。

4 懸置系統優化

4.1 優化目標

動力總成懸置系統的優化可從多個角度來選擇優化的目標函數。如以系統固有頻率合理匹配為目標、以能量解耦為目標、以振動傳遞率最小或支承處動反力最小為目標和以人體垂向振動加速度均方根值最小為目標等，或綜合以上多個設計指標進行多目標優化［7］。

理論上講當懸置系統的彈性中心與動力總成的質心重合時，動力總成懸置系統在各個方向上的振動完全解耦。但實際上由于受到懸置元件本身性能和整車布置空間的限制，一般難以實現。只能通過合理設計懸置參數以期使懸置系統各個自由度方向上的解耦達到相對最優。本文中以能量解耦為目標對該動力總成懸置系統進行優化。

4.2 設計變量

從式(2)動力總成懸置系統的振動微分方程可以看出，影響懸置系統隔振性能的量有質量矩陣、剛度矩陣和阻尼矩陣，它們涉及動力總成的質量與慣量參數、剛度和阻尼參數以及懸置元件的安裝位置和安裝角度等。在對動力總成懸置系統進行優化時一般不對系統的質量和慣量參數進行修改;懸置元件的阻尼對系統的振動影響很大，主要作用是降低系統的共振峰值，文中采用固定阻尼比，不將阻尼作為設計變量;懸置元件的安裝位置和安裝角度由于受到安裝空間的限制，不可能有大的改變，因此綜合考慮之后，以3個橡膠元件共9個剛度參數作為設計變量進行解耦優化。

4.3 約束條件

為防止運動干涉，該電動汽車動力總成懸置系統的質心位移要小于5mm。懸置系統的1階固有頻率要高于懸掛質量部分的固有頻率(一般為1～2Hz)和座椅的固有頻率(一般為3～4Hz)，以免發生共振。因此根據隔振理論，該動力總成懸置系統的1階固有頻率應大于。考慮到該電動汽車布置空間的限制，將懸置元件的坐標位置調整為表2所示的值，懸置元件的安裝角度不變。

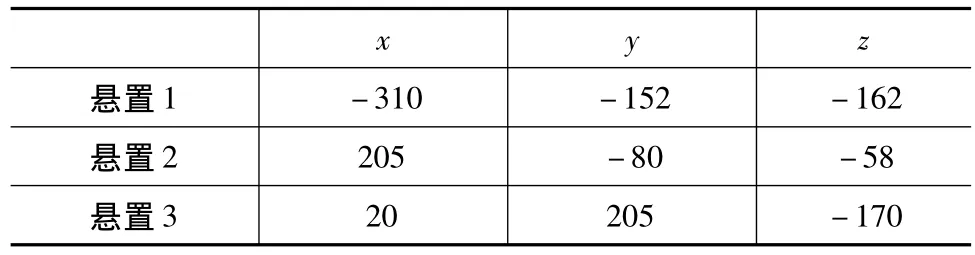
表2 懸置元件彈性中心坐標 mm

4.4 優化結果分析

運用ADAMS/Insight模塊采用3階響應面試驗設計對該電動汽車的動力總成懸置系統進行優化。首先在ADAMS/Vibration模塊下建立懸置系統能量解耦的6個設計目標，再將橡膠元件的9個剛度參數設為設計變量，然后導入Insight模塊進行計算，得到橡膠元件的剛度參數見表3。優化后懸置系統的固有頻率和能量分布百分比如表4所示。

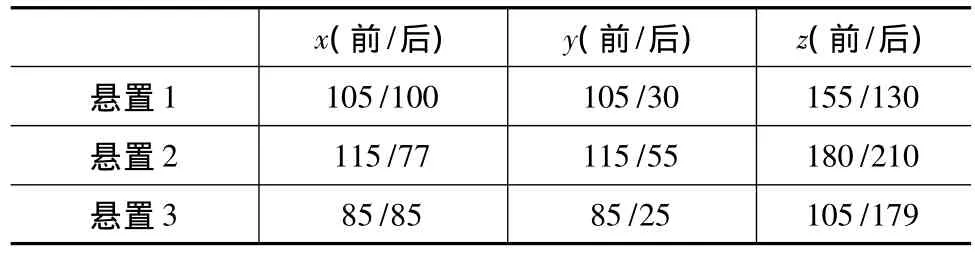
表3 優化前/后橡膠懸置元件的剛度 N/mm

表4 優化后懸置系統各階固有頻率和振動能量

從表4和表1的對比可知，優化前后固有頻率值變化并不大，但能量解耦情況卻有顯著改善，6階模態的解耦率都達到了90%以上。優化后的瞬態響應結果如圖9～圖16所示。

從計算結果可以看出，經解耦優化后，在電動汽車起步和制動兩種工況下動力總成懸置系統的瞬態響應情況得到了很大改善。下面從動力總成懸置系統Z向的瞬態響應情況加以說明。

由圖9～圖10可知，優化后動力總成懸置系統的質心Z向振動位移峰值由3.5mm降低到2mm，振動加速度峰值由10050mm/s2降低到8300mm/s2左右，起步和制動時的振動值都明顯降低，并且由于振動能量降低使振動的衰減加快。

由圖11～圖13可知，優化后3個橡膠懸置元件的Z向受力情況明顯改善，力的峰值和振動穩定后的值都明顯降低，振動也衰減得很快。

由圖14～圖16可知，優化后3個橡膠懸置元件的Z向位移變形明顯減小，振動衰減得很快。特別是第3個橡膠懸置元件的變形量減小得最多，由4mm降到2mm左右。

5 結論

采用動力學仿真分析軟件ADAMS的View、Vibration和Insight模塊對純電動汽車的動力總成懸置系統進行了仿真分析和能量解耦優化，優化后的能量解耦率很高，取得了很好的效果。通過對電動汽車急加速和緊急制動兩種工況進行瞬態響應計算獲得了該電動汽車的動力總成懸置系統的瞬態振動特性，經解耦優化后，動力總成懸置系統的瞬態響應特性得到了很大改善。這說明通過能量解耦的方法能很好地解決動力總成懸置系統的振動問題，為電動汽車動力總成懸置系統的設計提供依據。

［1］Jeong T，Singh R.Analytical Methods of Decoupling the Automo-tive Torque Roll Axis［J］.Journal of Sound and Vibration，2000，234(1):85-114.

［2］江合連.混合動力轎車動力總成懸置系統隔振與優化研究［D］.長春:吉林大學，2008.

［3］呂振華，范讓林.動力總成—懸置系統振動解耦設計方法［J］.機械工程學報，2005，41(4):49-54.

［4］上官文斌，黃天平，等.汽車動力總成懸置系統振動控制設計計算方法研究［J］.振動工程學報，2007，20(6):577-583.

［5］吳杰，上官文斌，等.動力總成懸置系統解耦布置的魯棒性分析［J］.振動與沖擊，2009，28(9):15-20.

［6］王珣，張立軍，王建.燃料電池轎車電動動力總成懸置系統動態特性分析［J］.汽車技術，2009(2):29-32.

［7］宋才禮.動力總成懸置系統隔振性能研究［D］.鎮江:江蘇大學，2009.

［8］余卓平，王建，等.燃料電池轎車動力總成懸置系統的優化設計［J］.機械設計，2009，26(7):50-53.

［9］Yu Yunhe，Naganathan Nagi G，Dukkipati Rao V.A Literature Review of Automotive Vehicle Engine Mounting Systems［J］.Mechanism and Machine Theory，2001，36:123-142.