發電機欠勵限制與失磁保護配合的分析
劉宏猷,邵富平,郝貴敏,熊 麗
(大唐河北發電有限公司馬頭熱電分公司,河北 邯鄲 056044)
在發電機勵磁系統和發電機保護中分別設有欠勵限制和失磁保護,勵磁調節器欠勵限制必須和失磁保護相匹配,任何操作或電力系統擾動都應保證欠勵限制先于失磁保護動作。DL/T 843-2010《大型汽輪發電機勵磁系統技術條件》中明確規定“欠勵限制的動作曲線應注意與失磁保護的配合”。
1 300MW機組失磁保護的整定計算
1.1 勵磁系統介紹
大唐河北發電有限公司馬頭熱電分公司(簡稱“馬頭發電公司”)300MW發電機組為東方電機廠產品,配套使用的是GEC-313勵磁控制系統,發電機勵磁方式為自并勵勵磁系統。由勵磁變壓器、勵磁調節柜、進線柜、整流柜(3面柜)、滅磁過壓保護柜(1面柜)等構成;勵磁調節柜內安裝的是勵磁控制器,是勵磁反饋控制的核心部分。整流柜內安裝的是由大功率晶閘管組成的三相全控整流橋,根據發電機勵磁電流的大小,可由若干個整流柜向發電機提供勵磁電流。滅磁過壓保護柜中安裝的是滅磁開關和非線性或線性滅磁電阻及過電壓保護裝置。
1.2 失磁保護整定的基本參數
根據9號機組短路計算書,相關數據如下。
基準容量SB=100MVA;系統聯系電抗Xs=0.072 8;發電機參數:暫態電抗X′d=0.256 8;同步電抗Xd=1.854 8;額定電壓UGN=20kV;額定視在功率SGN=353MVA;TA變比nTA=3 000;TV變比nTV=200;二次額定電壓Ugn=100V。
當發電機低勵或失磁時,發電機機端測量阻抗軌跡進入異步邊界阻抗圓,作為發電機進入異步運行狀態的判據:
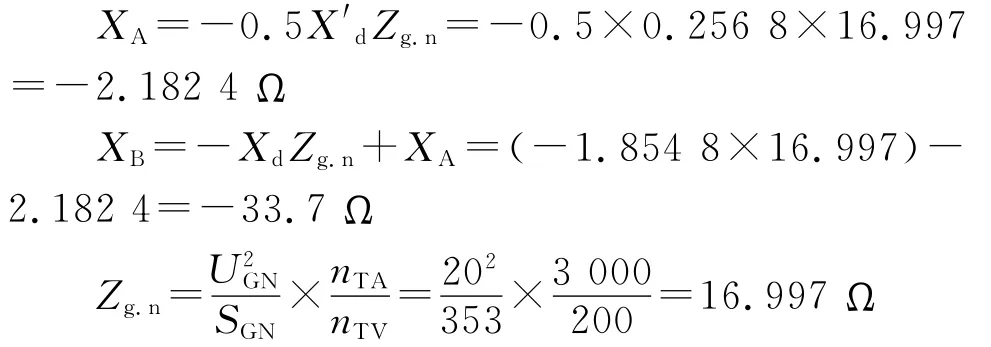
式中:XA為異步邊界圓和jX軸的第1交點的縱坐標整定值,Ω;XB為異步邊界圓和jX軸的第2交點的縱坐標整定值,Ω;Zg.n為發電機額定基準二次阻抗有名值,Ω。
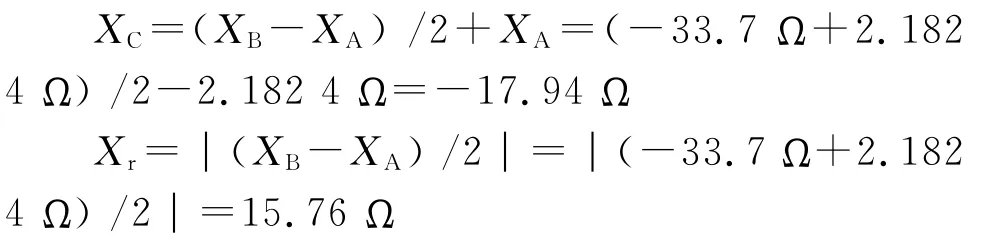
取XC=-17.94Ω,Xr=15.76Ω
失磁保護采用異步邊界阻抗圓如圖1所示。
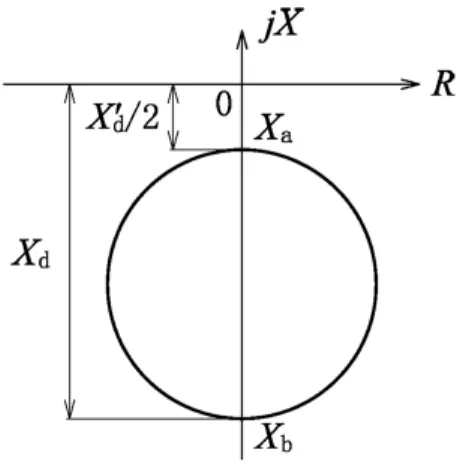
圖1 異步邊界阻抗圓
1.3 失磁保護機端三相電壓判據
取機端三相電壓,本判據主要用于防止由發電機失磁故障引發的廠用電系統不能正常工作,其三相同時低電壓動作判據為:UOP.3ph=0.95Ugn,根據省調涉網保護要求,機端電壓整定為95V。
2 發電機失磁保護及勵磁系統欠勵限制配合關系
2.1 發電機失磁機端測量阻抗變化
發電機從低勵或失磁開始到進入穩定異步運行,一般可分為低勵或失磁后到失步前、靜態穩定極限點、失步后的異步運行3個階段來分析。發電機由低勵或失磁開始到失步之前的階段,發電機發出的功率基本保持不變,是一個等有功功率過程,而無功功率在這段時間內由正值變為負值。隨著勵磁電流不斷下降,發電機的感應電勢逐漸降低,其功角特性曲線降低,使得功角增大,當功角被拉大到90°時,發電機處于靜態穩定極限點,由此產生了發電機由穩定向失步變化的轉折點。通過計算分析,可以得到靜態穩定邊界阻抗圓。隨后發電機失步,進入異步運行階段,這時由機端觀測的發電機等值阻抗為發電機的異步阻抗。異步阻抗與轉差率有關,并在一定范圍內變化,該范圍可包含在一個阻抗圓內,稱其為異步邊界阻抗圓。
2.2 靜態穩定極限阻抗圓、異步邊界阻抗圓與等有功阻抗圓的相對位置
從失磁開始到靜態穩定破壞前,機端阻抗的變化軌跡是一個阻抗圓,稱其為“等有功阻抗圓”(如圖2所示),該圓圓心為,半徑為US2/2P=0.16。
異步邊界阻抗圓的整定為:XA=-0.5X′d=-0.128 4,Xb=-Xd=-1.854 8。
靜態穩定極限阻抗圓(如圖2所示)的整定為:XC=XS=0.072 8,Xb=-Xd=-1.854 8。
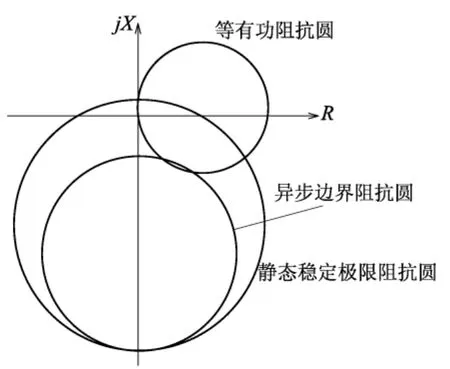
圖2 靜態穩定極限、異步邊界阻抗圓與等有功阻抗圓的相對位置
從圖2中可以看出,等有功阻抗圓與異步邊界阻抗圓在阻抗平面上有相交點。
2.3 失磁保護阻抗繼電器與欠勵限制線的特性配合分析
由于欠勵限制動作整定值是按照靜態穩定極限阻抗圓為條件設定,但其卻反應在P-Q平面上計算,而失磁保護是在R-X阻抗圓平面上。所以,為了使兩者參數配合,需要將兩者都歸算到同一個平面上。
2.3.1 以SB=353MVA為基準歸算20kV側電抗值
Xd=1.854 8×353/100×202/353=7.42Ω。
Xs=0.072 8×353/100×202/353=0.29Ω。
2.3.2 失磁保護靜態穩定極限阻抗圓在P-Q平面上的動作特性

失磁保護機端三相低電壓UOP=0.95×20=19 kV,則有圓心(0,597.5),半徑646.2。
作靜態穩定極限P-Q圓如靜態穩定極限阻抗圓,圓外為動作區;該圓與汽輪發電機的靜態穩定極限邊界完全一致。
2.3.3 失磁保護采用異步邊界阻抗圓時與欠勵限制線的配合
0.5X′d=0.5×0.256 8×202/100=0.51Ω,Xd=1.854 8×202/100=7.42Ω。
異步邊界阻抗圓(如圖3所示)為:
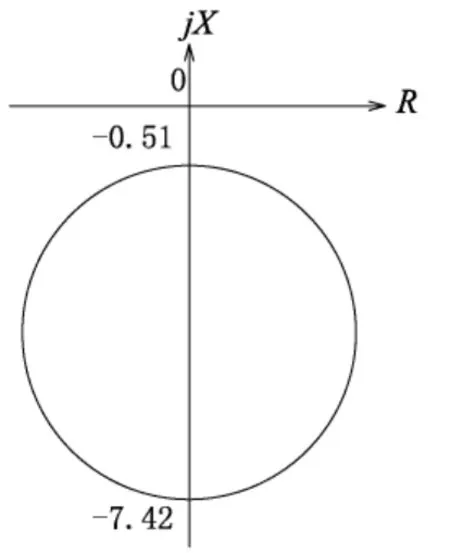
圖3 異步邊界阻抗圓
圓心[0,-(7.42+0.51)/2]=(0,-3.97),半徑(7.42-0.51)/2=3.46。
異步邊界阻抗圓的方程式為:R2+(X+3.97)2=3.462,即R2+X2+7.94X+3.79=0。
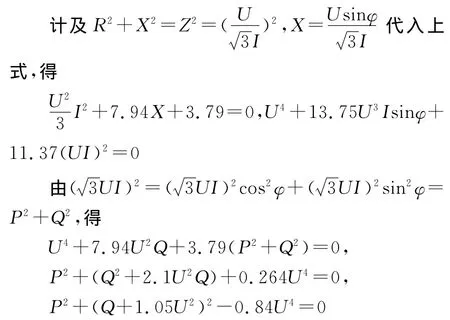
仍設失磁保護機端三相低電壓:UOP=0.95×20=19kV
則上式P2+(Q+379.1)2=330.92
因此異步邊界P-Q圓為圖4中的圓③:圓心(0,-379.1),半徑330.9。
如圖4所示,在P-Q平面上,欠勵限制線(圖4中曲線②)與靜態穩定極限阻抗圓和異步邊界阻抗圓均實現了合理配合,相對而言異步邊界圓的裕度更大。

圖4 靜態穩定圓、異步圓與欠勵限制線的配合
3 結論
通過介紹馬頭發電公司勵磁系統欠勵限制和發電機失磁保護的定值整定方法,分析了勵磁系統欠勵限制和發電機失磁保護之間的配合關系。從理論上論證了馬頭熱電公司9號機組勵磁系統欠勵限制和發電機失磁保護之間有很好的配合關系。
[1] 王維儉.電氣主設備繼電保護原理與應用[M].2版.北京:中國電力出版社,2002.
[2] 張保會,尹項根.電力系統繼電保護[M].北京:中國電力出版社,2005.
[3] 高春如.大型發電機組繼電保護整定計算與運行技術[M].北京:中國電力出版社,2005.

