基本過程能力指數的分析與應用問題研究
韓亞利
(長沙航空職業技術學院,湖南 長沙 410124)
在生產過程的質量分析與控制中,計算與評價過程能力指數是一項非常重要的工作。特別是近年來,隨著計算機技術的迅速發展,開發了很多質量管理和質量控制軟件,使得在計算過程能力指數值時,所需要的大量數據的實時收集、計算和分析,可以借助于計算機軟件來輕松地實現,極大地促進了過程能力指數的理論研究和在生產實際中的應用。
過程能力(Process Capability,PC)以往稱工序能力,現已根據ISO 標準規定,統一稱為過程能力,是指在生產過程處于穩定狀態時,該過程所生產的產品能滿足質量要求的能力。而過程能力指數(Process Capability Index,PCI)則是將過程能力量化后的評價標準,表示過程能力滿足質量技術標準(產品規格、公差)的程度。
經過長期的理論研究和實踐,從事數理統計質量控制的研究人員提出了許多種過程能力指數。根據文獻的不完全統計,目前已在實踐中應用和正在進行研究的單變量過程能力指數多達20 多種,多變量過程能力指數也有7 種。但從研究的原理和過程來看,這些過程能力指數都是從Cp、Cpk、Cpm和Cpmk等4個基本指數的基礎上發展、變化而來的[1]。它們之所以被稱為基本指數,首先,是因為它們是最早提出來的(1986年,美國質量專家V.E.Kane 在公開發表的文獻中就系統地介紹了這4個指數)、也是最簡單的指數(單變量指數);其次,還因為這4個指數都是建立在過程特性值服從最常見的正態分布假設之上的,是當生產過程處于穩定狀態時進行過程能力分析與評價的、最常用的幾個指數。因此,正確理解、把握、解釋這幾個基本過程能力指數的定義、概念和應用特點就顯得尤為重要。
1 過程能力指數
對于穩定受控的生產過程,由于不可避免地存在各種隨機因素的作用,其過程特性值總呈現一定的分散性。在一般情況下,過程特性值服從正態分布N(μ,σ2),其中μ 為過程特性值的總體均值,σ 為過程特性值的總體標準差。在正態分布曲線圖上,T=Tu- Tl為技術規格的公差幅度,Tu、Tl分別表示上、下規格界限,技術規格的公差中心
1.1 第一代過程能力指數Cp、Cpk
(1)過程能力指數Cp。美國著名質量專家朱蘭(J.M Juran) 在1974年首先提出了用統計控制狀態下的6σ 表示的過程能力指數Cp,其定義式為:

在Cp定義式中,T = TU- TL反映產品質量的設計要求,總體標準差σ 反映了過程特性值的分散程度,可通過計算樣本標準差S 來估計。所以Cp定義式將6σ 與T 比較,就反映了過程質量滿足產品質量設計要求的能力,定量的表征了該工藝過程滿足技術規范要求的能力。Cp值越大,表明該工藝過程滿足技術規范要求的能力越高,但對設備和操作人員的要求也越高,相應的經濟成本也越大。
Cp就是通常所說的過程能力指數,該指數討論的是過程特性值均值μ(分布中心)和技術規格的公差中心M 重合一致的情況,即μ=M,但這只是一種理想的狀態。因此,Cp值僅表示工序過程能力的潛力,又稱為潛力過程指數。
(2)實際過程能力指數Cpk。在實際生產過程中,經常有分布中心與公差中心不重合的情況,即μ≠M有偏移量ε,如圖1 所示。
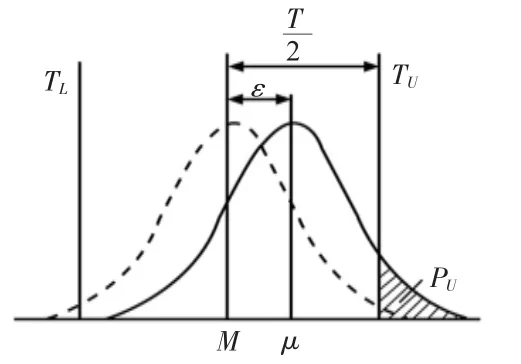
圖1 μ≠M 有偏移量ε 時的情形
從圖1 可得知,當μ≠M 有偏移量ε 時,不合格品率PU明顯增大,過程能力減小。此時,Cp已不足以反映有偏移的實際情況,需要加以修正。
美國質量專家V.E.Kane 在1986 提年出了需要定義一個校正因子來表征偏移量的大小,并將修正后的指數Cpk定義為:
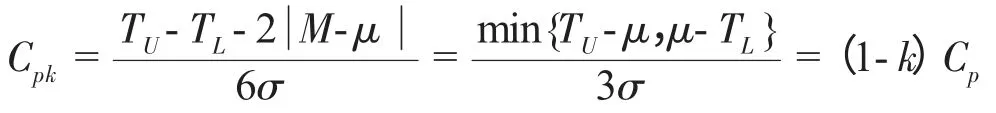
顯然,偏移系數0≤k≤1。即:當μ≠M 時,Cpk CPk的定義式充分考慮了分布中心μ 與公差中心M 之間的位置關系,克服了Cp指數的缺陷。因此,Cpk在實際生產過程中比Cp應用更多,很多質量研究學者又稱其為實際過程能力指數[2]。 雖然Cpk考慮了μ 偏移M 的程度,但對于μ 偏離目標值T 的情況仍無法反映。無論Cp還是Cpk的定義式,對于給定區間(TL,TU)內的μ 值,當σ →0 時,Cp和Cpk都會發散至無窮大,因此Cp和Cpk不能很好的用于過程集中程度的度量。針對指數Cp和Cpk的缺點,一些質量研究學者又在此基礎上進行了修正,并引入田口損失函數期望值的概念,將其定義為“田口指數”CPm: 其中:σ'2= E[(Y-T)2],表示Y 偏離目標值T 的方差的期望。 由于田口指數CPm的設計考慮到μ 與T 之間的關系,故無論使過程方差變大,還是過程偏離目標變大,都會引起CPm的減小,因此,CPm能綜合反映過程偏離目標的離散程度。 該指數把顧客期望的理想值(也即目標值)引入進來,體現了Taguchi 質量管理思想——產品偏離目標值就會有質量損失。所以CPm在反映過程期望損失的能力上要明顯優于CP和CPk,通過計算CPm可以對過程的經濟性進行客觀的估計。這就是CPm與Cp、Cpk的本質區別。 Pearn Kotz 和Johnson 將CPk和CPm的 優 點 相 結合,于1992年提出了過程能力指數CPmk的定義: 由定義可知,CPmk同時考慮了μ 與M 及T 之間的關系。Peam Kotz 同時還證明,當T=M 且μ=T 時,CPmk指數比CPk和CPm都靈敏,即CPmk的下降速度最快。因此,CPmk指數能同時反映過程的不合格品率和期望損失[2]。 CPmk又稱為混合指數,由CPk的分子與CPm的分母混合而成,其對過程能力的綜合評價效果要好于CPk和CPm。但是,研究表明在很多情況下該指數與實際生產過程也還是有一些差距[3]。 對過程能力評價的基本原則是:既要考慮生產過程有充足的過程能力,又要考慮生產過程有合理的經濟性指標。在一般情況下,由抽樣采集的樣本數據計算出過程能力指數后,即可根據Cp、Cpk值對過程能力進行評價,如表1 所列;如果存在偏移系數k,則需要根據Cp、Cpk值的大小對某些參數進行處理,如表2 所列。 表1 過程能力指數Cp 值評價標準 表2 存在偏移系數k 時的處理 上述Cp值評價標準只是傳統的一般要求,只能作為實際工作的參考,其它幾個過程能力指數的評價標準可參考有關文獻資料。 需要說明的是,所謂過程能力不足或過高,都是針對特定生產制造過程以及特定產品的特定工序過程而言,不應理解為統一的模式。例如,當Cp叟1.33時,過程能力充分滿足質量要求,故在ISO9000 標準中要求Cp叟1.33;而在一些企業推行的六西格瑪管理模式中,則要求Cp值達到2,這是現代企業的高標準、嚴要求,也是高新技術發展的必然。 由已知條件計算可得,公差中心M=20.007 5;又已知分布中心向右偏移,偏移量ε=偏移系數k=0.2,過程能力指數Cp=0.933。 由表1 所知,Cpk=0.933,在1.0>Cpk叟0.67 范圍內,屬于Ⅲ級過程能力,表現為該工序的過程能力不足,質量保證能力較差;應分析原因,采取工藝措施,提高過程能力以保證產品質量。具體有以下幾種途徑: (1)針對零件設計功能,適當加大內孔公差范圍,減少工序加工難度; (2)選用高精度機床設備,減少偏移量ε,提高工序加工精度; (3)查找原因,確定質量改進方向,減少過程特性值的分散程度σ。 隨著計算機技術的發展,過程能力指數的計算和分析已非常簡便、快捷,但在實際工作中,質量管理人員還是會出現一些技術問題,使得他們不能很好地利用這一質量工具來分析、評價過程能力。本文主要涉及與過程能力指數的定義、特征有關的兩個技術問題的處理。 在實際生產現場的質量控制中,有些質量管理人員為了節省抽樣時間,只抽取少量的樣本數據就計算過程能力指數,這樣往往會導致其分析結論和生產過程的實際情況產生很大差異。 根據數理統計學原理,這種基于樣本得到的過程能力指數估計值本身就會產生估計偏差。特別是,當抽取的樣本容量n 太小、且樣本中還存在某一個或幾個異常值時,就將很難保證抽樣結果反映出隨機性變量的主要特征。即這些異常值的存在會影響到數據分布的正態性,對樣本均值和標準差的計算帶來很大誤差,從而使過程能力指數嚴重失真。 當樣本容量n 很小時,過程能力指數的置信區間也會很大。我們可以根據抽取的樣本數據,計算當過程能力指數的估計值=1 時,不同的樣本容量n所對應的CP置信區間,如表3 所列。 表3 與樣本容量n 對應的Cp 置信區間 事實上,在小樣本條件下(n 小于20 ~ 30)難以判定過程特性值數據分布的正態性,也很難說明在抽樣時,過程是否處于穩定或受控狀態,計算出的過程能力指數值可能和實際值有很大的偏差。因此,有些統計質量學專家質疑、反對在小樣本條件下計算過程能力指數[4]。 在抽樣的過程中,難免會發現有些抽樣數據明顯與其它數據不同(異常值)。因此,在計算和分析過程能力指數時,應結合使用控制圖等質量工具,通過數據分布檢查有無異常波動或異常值存在。異常波動對質量的影響大,但采取措施不難消除,故在過程中一旦發現異常值,就應該盡快追蹤其原因,采取措施加以消除,并納入標準,保證它不再出現。若找不到導致異常值的原因,則不能隨便剔除抽樣數據。 基本過程能力指數的定義都設定過程特性值服從正態分布,當數據分布為非正態分布時,基本過程能力指數定義的理論基礎就不成立,此時計算過程能力指數是毫無意義的。因此,在得到樣本數據后,首先就要檢查數據分布是否為正態分布。有些現場質量管理人員在計算過程能力指數時,往往會忽視對數據分布的正態性檢驗,直接就根據抽取的樣本數據計算均值和標準差,這樣往往會造成誤判。 當過程特性值不服從正態分布時,對基本過程能力指數進行修正的理論研究成果很多,但這些非正態分布總體下的指數設計方法,均具有一定的主觀性,大多比較抽象,不便于實際使用者掌握。但是,對于某些由于特殊的工藝原因導致數據分布非正態的情況,為了仍然能夠應用過程能力指數表征工藝過程的質量保證能力水平,可通過一些簡單的轉換方法,盡量把非正態數據轉換成正態,然后根據轉換后的數據計算過程能力指數[5]。 等效指數轉換是一種能應用于生產實際的、較為簡便的方法。等效指數轉換的主要思路是通過計算過程特性值的不合格品率,以在同樣不合格品率的情況下,當質量特征值的均值和目標期望值重合時的過程能力指數作為等效過程能力指數。這樣,過程能力指數就和過程特性值分布類型無關,且只與工藝成品率對應。對于總體均值與公差中心不重合時存在的偏離,也可以計算得到存在偏離時的等效過程能力指數。用這種方法處理非正態數據比較直觀,容易理解,具體的轉換方法可參考有關文獻資料。 科學地計算和分析過程能力,可以清楚地了解和評價過程質量水平,對于產品設計、工藝制定、計劃安排、生產調度和技術改造等方面都具有重要意義,同時也是一項非常復雜的、技術難度很高的專業性工作。本文通過對上述幾個基本過程能力指數的定義、特點的研究,給出了各種指數的應用特征和范圍,能夠為生產現場的質量管理人員進行過程能力分析、評價提供指導,也為建立計算機系統模塊提供了清晰的數學模型和相應的數據支持。 [1]劉光第.質量管理學(第二版)[M].北京:清華大學出版社,2003. [2]龔益鳴.質量管理學[M].上海:復旦大學出版社,2000. [3]錢中侯,張公緒.質量專業理論與實務[M]. 北京:中國人事出版社,2001. [4]張公緒.質量專業工程師手冊[M].北京:企業管理出版社,1994. [5]張公緒,孫 靜.新編質量管理學(第二版)[M].北京:高等教育出版社,2003.1.2 第二代過程能力指數CPm
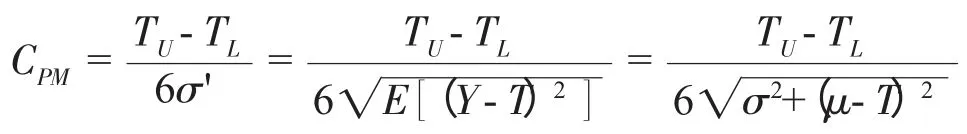
1.3 第三代過程能力指數CPmk
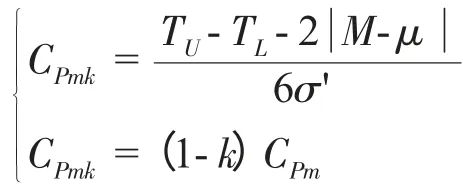
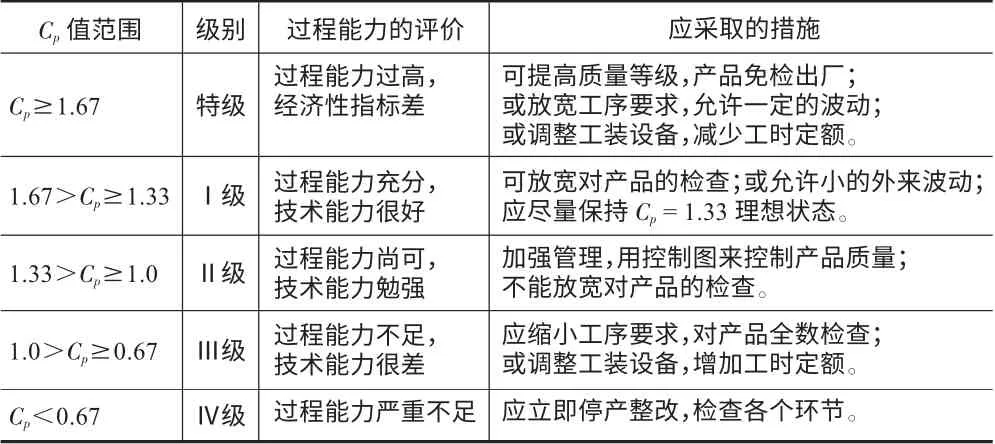
2 過程能力的分析和評價

3 幾個技術問題的處理
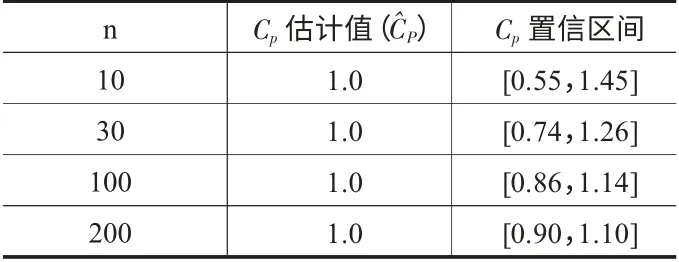
3.1 樣本容量和異常值的處理
3.2 非正態分布的等效指數轉換
4 結束語

