OFDM系統中基于導頻的信道估計算法性能分析
馬玉峰
(沈陽理工大學 遼寧 沈陽 100159)
0 引言
正交頻分復用 (Orthogonal Frequency Division Multiplexing,OFDM)具有高速的數據傳輸能力、高效的頻譜利用率和抗多徑干擾能力,因而在無線通信領域被廣泛關注。由于無線信道的時變特性引起多徑衰落和多普勒效應,破壞OFDM系統中子載波之間的正交性,導致載波間干擾(ICI)限制了OFDM系統在高信噪比下的性能,使OFDM傳輸系統的性能大幅度下降。為了在接收端準確地恢復發送端所發送的原始信號,通常需要根據接收信號對信道進行估計。本文采用基于導頻的信道估計,分別對 LS(最小平方誤差)估計器,LMMSE(線性最小均方誤差)估計器及其簡化算法進行了分析研究。分析了各種信道估計器的性能,并且研究了如何通過參數調整來提高信道估計器的性能以降低信道對整個系統的影響。
1 信道估計算法原理分析
1.1 基于LS的信道估計算法研究
最小平方LS(Least-Square)信道估計就是從最小平方的意義上得到的信道估計器,設接收端在導頻點處接受到的信號為Y,發送的信號為X,噪聲為n,則有:

在不考慮AWGN的影響的情況下,LS算法的估計值為:
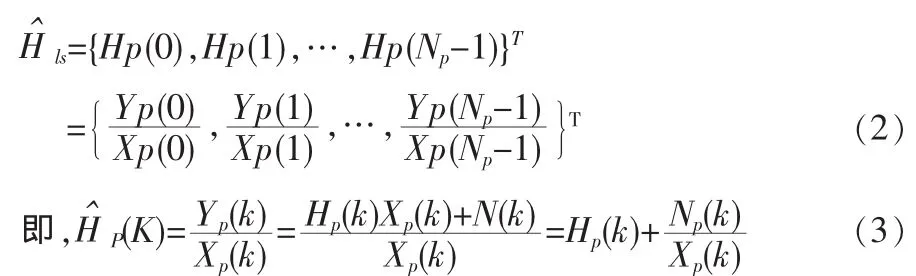
1.2 基于LMMSE準則的信道估計算法研究
在噪聲η與信號X不相關的條件下,信道傳輸函數在最小均方誤差意義下的最佳信道估計器是:

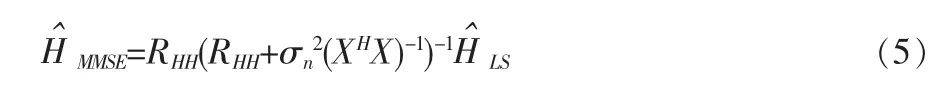
信道響應的MMSE估計在進行最優化問題求解時考慮了噪聲的影響,所以信道估計的均方誤差較小。但由于MMSE估計的運算量很大,在實現過程中要知道信道的統計特性,尤其是維數增加時,矩陣的求逆運算量非常大,在實際應用中受到了一定的限制。
1.3 基于低秩LMMSE的信道估計算法研究
假設在一個OFDM符號內導頻信號位置為Lp={in,0≤n≤Np-1},Np為一個OFDM符號內的導頻信號數,用Xp=diag[xi0,xi1,…,xiNp-1]表示導頻信號矩陣,yp=[yi0,…,yiNp-1]T表示接收到的導頻信號,則導頻位置信道頻率響應的最小二乘(LS)估計包括數據位置在內的信道頻率響應的LMMSE估計為:

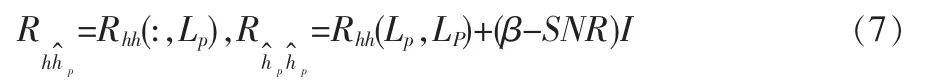

其中,Q1,Q2為酉矩陣,D為對角陣,其對角線的奇異值按照從大到小排列。
采用低秩估計(秩為r)的信道頻率響應為:
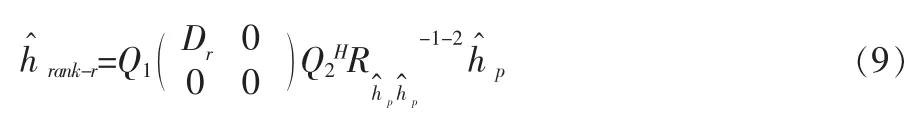
其中Dr為D的左上角r×r矩陣,也是一個對角陣,包括了r個最大的奇異值。當且僅當數據為全導頻的情況下有此時通過化簡并整理可以得到:

Δr也是對角陣,對角線上的元素為:
下面我們來比較LMMSE估計算法和低秩估計算法的計算量。兩者都要先由估計導頻位置的信道最小二乘估計決定,所需要的乘法次數都為Np。所不同之處在于式(6)和式(7)的區別,由于式(6)中的R和式(7)中的都是可以預先計算好的,不必每一次估計都要重新計算一次,所以這兩個預計算的計算量不必計算在內。由于是滿秩的,秩為 r,所以(7)式的乘法次數為 N(N+NP),而(7)式的乘法次數為 r(N(N+NP))。 總的來說,LMMSE 估計算法的計算量為每估計一個OFDM符號的信道需要N0+N(N+NP)次乘法,低秩估計算法的計算量為每估計一個OFDM符號的信道需要NP+r(N+N0)次乘法。顯然,低秩估計算法的計算量比LMMSE估計算法的計算量少。
2 仿真結果分析
仿真環境為每幀100個OFDM符號,共有100×128個星座映射符號;16QAM調制下,1個星座映射符號包含4個bit,載頻為 2GHz,帶寬1MHz,子載波數128個,cp數為 16,子載波間隔為7.8125kHz,一個OFDM符號長度為128μs,cp長度為16us,調制方式采用16QAM調制方式,最大多普勒頻率為132Hz,多徑信道為5徑,功率延遲譜服從負指數分布exp(-t/trms),trms=(1/4)*cp時長,各徑延遲取為delay=[0 2e-6 4e-6 8e-6 12e-6],導頻符號間隔為10。
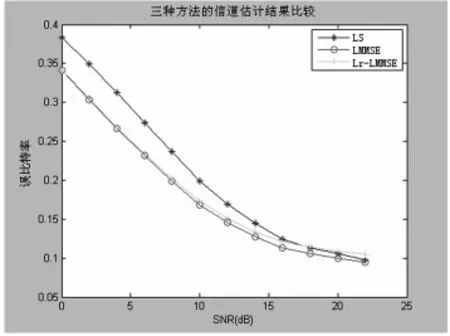
圖1 三種方法的信道估計結果比較
如圖1所示,在信噪比相對較小的情況下可以發現基于LS(最小平方)信道估計的方法效果明顯較差,當信噪比大于15dB并小于20dB時的時候三種方法基本估計結果相同,而當信噪比大于20dB時LS(最小平方)信道估計方法更接近于基于LMMSE的信道估計方法,但由于其復雜度高而被人們所忽視。從圖1中還可以得到基于低秩的LMMSE信道估計算法當在信噪比大于10dB后誤碼率明顯大于沒有降秩的LMMSE信道估計方法,但由于在每估計一個OFDM符號時所需要的計算量比LMMSE估計和LS估計的計算量要少,復雜度要低,而且誤差性能也比基于LS的信道估計方法好,所以低秩LMMSE的估計方法更優越。
3 結束語
本文研究了三種基于導頻的信道估計技術:基于最小平方LS(Least-Square)信道估計,基于LMMSE準則的信道估計,基于低秩LMMSE的信道估計,并對這三種估計算法各自的優、缺陷做了進一步的分析與比較。從上面分析可以看出,LMMSE準則的算法復雜度遠遠高于LS準則。而性能上MMSE準則優于LS準則。而基于低秩的LMMSE的信道估計方法無論從復雜度還是性能上都比較突出。因此在實際應用時就根據具體情況采用不同的方法。
[1]王文博,鄭侃.寬帶無線通信OFDM技術[M].人民郵電出版社,2003:10-67.
[2]劉艷國,余國華.信道估計在OFDM系統中的應用[J].通信與廣播電視,2008,01.
[3]李小文,潘迪.OFDM系統的導頻信道估計方法的設計與性能分析[J].2009,04.
[4]Sinem Coleri,Mustafa Ergen,Anuj Puri,et al.Channel estimation Techniques based on pilot arrangement in OFDM Systems[J].IEEE Transactions on Broadcasting 2002,48(3):223-229.
[5]任大盂,張曙.一種快變信道下OFDM系統的Kalman信道估計算法[J].哈爾濱工程大學學報,2007(11):1268-1272.

