基于平方和的一類不確定非線性系統(tǒng)的魯棒穩(wěn)定性

陳少燕（廈門大學，福建 廈門 361005）

1 引言

不確定系統(tǒng)的魯棒分析與綜合問題一直以來都是控制界的研究熱點，目前大多采用Lyapunov穩(wěn)定理論來研究，其中二次穩(wěn)定是一個非常重要的概念和方法[1]。但是，二次穩(wěn)定性要求對所有的不確定參數(shù)，存在一個公共的Lyapunov函數(shù)，這種要求過于苛刻，因此二次穩(wěn)定是一個較為保守的概念[2]。如果能夠根據(jù)變化的參數(shù)選取不同Lyapunov函數(shù)，就可以大大降低系統(tǒng)設計的保守性。因此，不少學者通過將Lyapunov變量參數(shù)化來獲得一類依參數(shù)Lyapunov函數(shù)的穩(wěn)定條件[3-5]。相對于單一Lyapunov函數(shù)的穩(wěn)定條件，其系統(tǒng)保守性得到明顯改善。但是以上方法運用于線性模型或者模型近似線性化上，這樣處理上丟失了原模型中的非線性部分，得到的結果精度較低。

近年來，由于SOS理論的提出，許多學者采用SOS理論分別對非線性系統(tǒng)的魯棒性和穩(wěn)定性分析、幾何定理證明、量子信息論、吸引域估計等問題進行了研究。SOS理論在處理非線性控制問題過程中的優(yōu)勢在于：（1）非凸非線性控制問題可以轉化為凸優(yōu)化問題；（2）不需要對原始模型進行過多的化簡近似；（3）得到的控制器是關于狀態(tài)變量的多項式方程，便于工程執(zhí)行。

本文針對一類不確定非線性系統(tǒng)，利用SOS理論結合Lyapunov函數(shù)[6]的方法，給出了使系統(tǒng)穩(wěn)定的非線性控制器設計方法，最后利用SOSTOOLS[7-9]工具箱求解出控制律。本文將用SOS理論方法彌補以往設計方法中不能給出系統(tǒng)有效控制器設計和求解方法的不足。此外，采用的SOS理論方法彌補了文獻[6]中LMI不能計算全局解的不足。

2 基于SOS理論的非線性狀態(tài)反饋控制器設計

定義1[6]：對于多項式f(x)，如果存在一組多項式fi(x) 滿足：

則稱多項式f(x)允許平方和分解，或稱多項式f(x)是SOS。

引理2[6]：多項式f(x)（d e g (f(x) )=2d）是SOS，當且僅當存在半正定矩陣Q≥0及單項式向量Z(x)（ d eg(Z(x))≤d），使得：

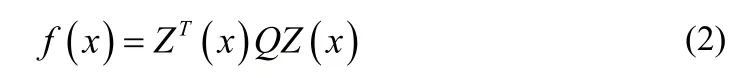
考慮一類不確定非線性系統(tǒng)

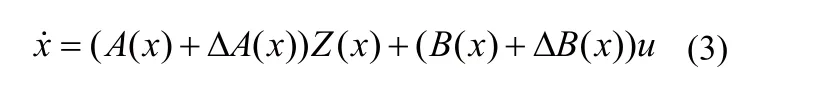
這里A(x)，B(x)為含x的多項式矩陣， ?A(x)和?B(x)分別是函數(shù)矩陣A(x)和B(x)的不確定項；Z(x)為含x的N×1多項式，并且滿足假設3。

假設3[6]：當且僅當x=0時，Z(x)=0 。

定義矩陣函數(shù)M(x)為N×n的多項式矩陣，Mij(x)是矩陣函數(shù)M(x)第(i,j)個元素，定義為：

其中i= 1 ,L ,N,j= 1,Ln。

假設4[10]：

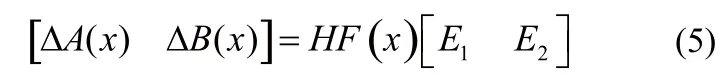
其中：F(x) ∈ ?s×s，其滿足不等式(6)：

其中：I是適當維數(shù)的單位矩陣；H∈ ?n×s、E1∈?s×N和E2∈?s×m是 已知的定常數(shù)矩陣。

為找到一個狀態(tài)反饋控制器u=k(x) =F(x)Z(x)，使得系統(tǒng)在平衡點x=0穩(wěn)定，所以我們提出定理7。下面的引理對定理7證明有關鍵性作用。

引理5[11]：已知適當維數(shù)的矩陣H、E和Y，其中Y是對稱矩陣，矩陣不等式：

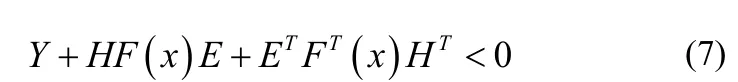
對所有滿足條件(6)的F(x)都成立，當且僅當存在一個標量ε> 0，使得

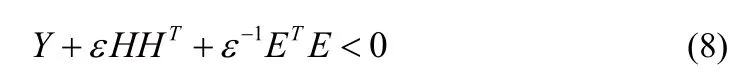
引理 6[12]：（S c h u r補引理）對于非線性對稱矩陣Q(x) =QT(x)、R(x) =RT(x)和S(x)，矩陣不等式

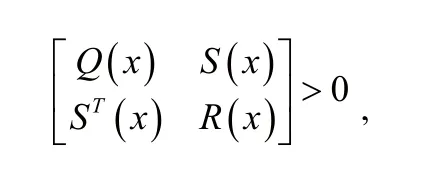
等價于R(x)>0 ，Q(x) ?S(x)R?1(x)ST(x)>0 。

定理7：對于系統(tǒng)(3)，假設存在對稱常數(shù)矩陣P，多項式矩陣函數(shù)K(x)，常數(shù)ε1>0、ε3>0、ε4>0及正定函數(shù)ε2(x)，使得下列矩陣表達式是SOS，

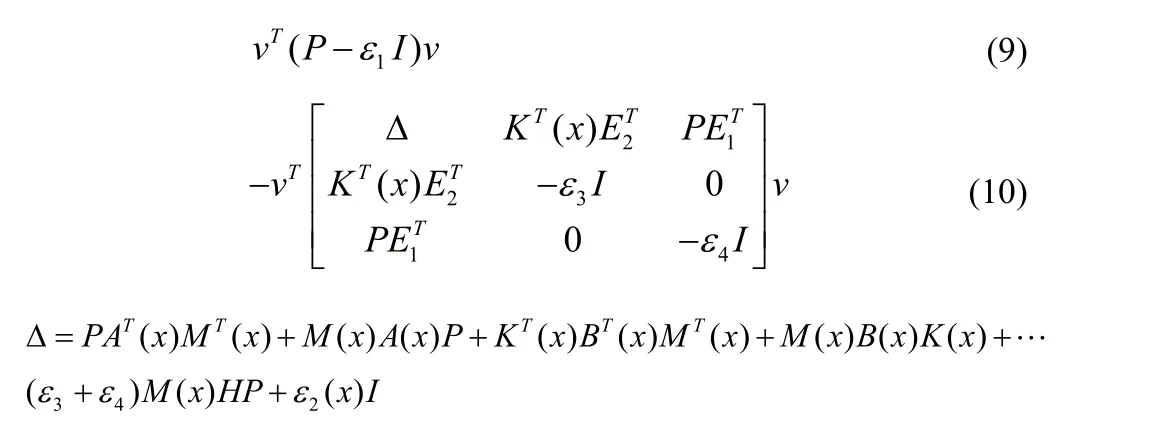
其中：v∈?N，則閉環(huán)系統(tǒng)是穩(wěn)定的，控制器

是系統(tǒng)(3)的一個狀態(tài)反饋控制器。若當x≠0，則ε3(x) > 0，那么閉環(huán)系統(tǒng)全局漸近穩(wěn)定。

證明：假設存在對稱常數(shù)矩陣P和多項式矩陣函數(shù)K(x)滿足式（9），（10）。定義：

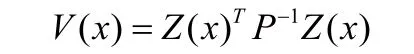
下面我們要證明V(x)是下面閉環(huán)系統(tǒng)的李亞譜諾夫函數(shù)。

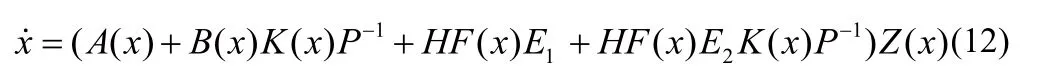
由引理2，條件(9)說明P和P?1對于所有的x都是正定的，所以V(x)也是正定的。沿閉環(huán)系統(tǒng)(12)的任意軌跡，V(x)的時間導數(shù)是：

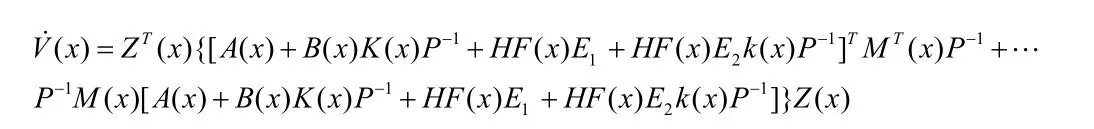
整理上式，得：

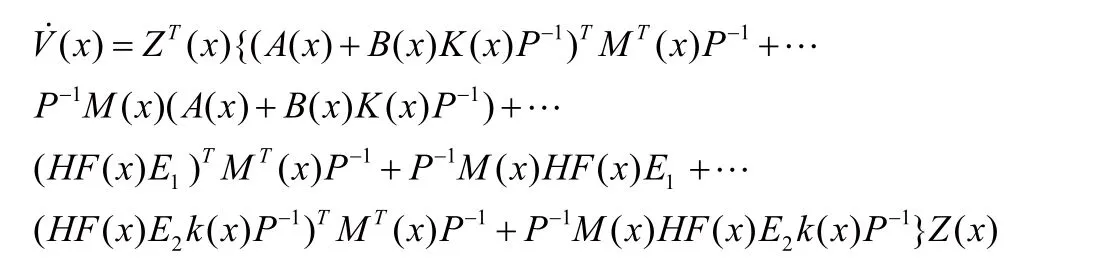
利用引理4和5，可得：

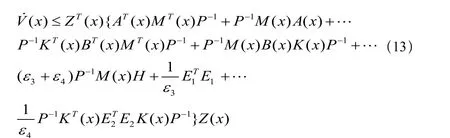
由(10)可知

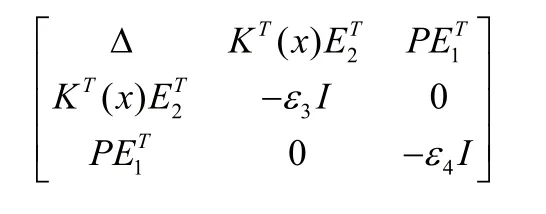
其中，

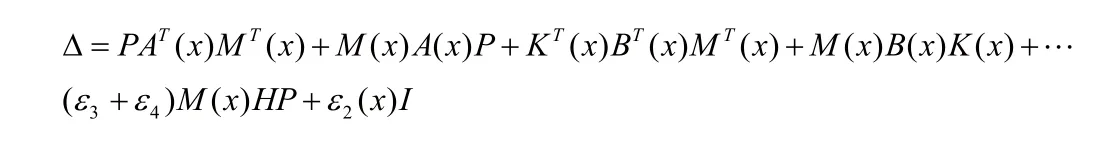
是半負定的。利用引理6展開后，再左右同乘P?1，可得到式(13)是半負定的。因此(x)≤0，所以V(x)是該閉環(huán)系統(tǒng)的Laypunov函數(shù)，閉環(huán)系統(tǒng)(12)是穩(wěn)定的。如果式(10)中，當x≠0，ε3(x) > 0 ，即V(x)的時間導數(shù)是負定的，閉環(huán)系統(tǒng)(12)全局漸近穩(wěn)定。

3 仿真實例

考慮如下不確定系統(tǒng)：

利用定理6設計狀態(tài)反饋控制器，可得

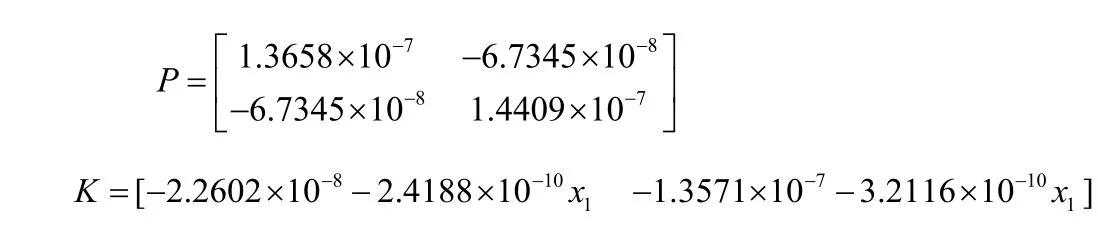
狀態(tài)反饋控制器：

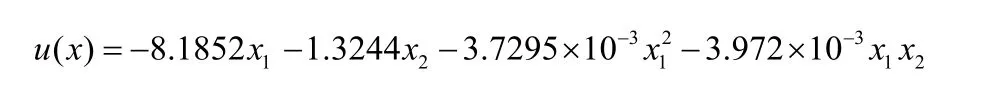
圖1為閉環(huán)系統(tǒng)漸近穩(wěn)定的系統(tǒng)狀態(tài)向量的時間響應圖。

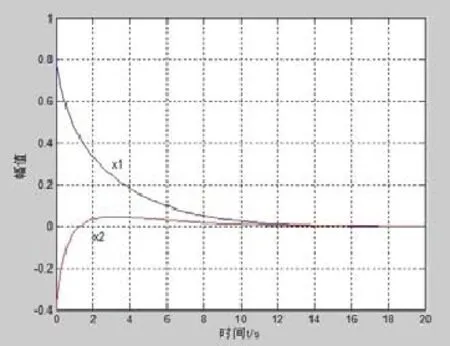
圖1 系統(tǒng)狀態(tài)向量的時間響應圖

從圖1中可以看出用基于SOS理論的方法設計非線性狀態(tài)反饋控制器可以使不確定非線性系統(tǒng)達到穩(wěn)定。

4 結論

針對一類不確定非線性系統(tǒng)，利用SOS理論結合Lyapunov函數(shù)的方法，給出了使系統(tǒng)穩(wěn)定的非線性控制器設計方法。利用SOS理論方法不需要對原始模型進行過多的化簡近似，得到的控制器是關于狀態(tài)變量的多項式方程，便于工程執(zhí)行。這彌補了以往設計方法中不能給出使系統(tǒng)有效的控制器設計和求解方法的不足。此外，采用的SOS理論方法彌補了LMI不能計算全局解的不足。仿真結果表明，本文提出基于SOS理論的狀態(tài)反饋控制器設計方法是有效的。

[1]黃琳.穩(wěn)定性與魯棒性的理論基礎[M].北京:科學出版社,2003.

[2]俞立.魯棒控制——線性矩陣不等式處理方法[M].北京:清華大學出版社,2002.

[3]Geromel J C, Korogui R H. Analysis and synthesis of robust control systems using linear parameter dependent Lyapunov functions[J].IEEE Trans on Automatic Control,2006,51(12):1984-1989.

[4]Oliveira Ricardo C L F. LMI conditions for robust stability analysis based on polynomially parameter-dependent Lyapunov functions[J].Systems and Control Letters,2006,55(2): 52-61.

[5]歐陽高翔,倪茂林,孫承啟.基于依參數(shù)Lyapunov函數(shù)的不確定系統(tǒng)魯棒穩(wěn)定控制[J].控制與決策.2008,23(12):1432-1440.

[6]S. Prajna, A. Papachristodoulou, and Fen Wu. Nonlinear control synthesis by sum of squares optimization: a Lyapunov-based approach[C].Proc.of the 5th Asia Control Conference, 2004, pp. 157-165.

[7]Prajna S, Papachristodoulou A, Seiler P, et al. Sostools: Sum of squares optimization toolbox for Matlab[R].California: California Institude of Technology,2004.

[8]Parrilo P A. Structured semidefinite programs and semialgebraic geometry methods in robustness and optimization[D].California: California Institute of Technology,2000.

[9]S. Prajna, A. Papachristodoulou, and P. A. Parrilo. Introducing SOSTOOLS:A general purpose sum of squares programming solver[C].Proc. Of the 41st IEEE Conference on Decision and Control, Las Vegas, Nevada USA,2002,741-746.

[10] Sing Kiong Nguang, Minyue Fu. Robust Control of Systems with Both Norm Bounded and Nonlinear Uncertainties[C].Proceedings of the 32nd Conference on Decision and Control 1993:2561-2566

[11]L. Xie. Output feedback H∞ control of systems with parameter uncertainty[J].Int. J. Contr., 1996,63(4):741-750.