基于信任度函數的認知無線電頻譜感知算法研究

李 轉，任旭虎

(中國石油大學(華東)信息與控制工程學院,山東 青島266555)

認知無線電CR(Coynitive Radio)技術能夠感知并分析某個特定區域的頻段，找出適合自己通信的“頻譜空洞”，利用某些特定的技術來處理利用合適的頻段，使其在不影響已有的通信系統的前提下進行工作[1]。如何進行高效的無線頻譜分析和估計是認知無線電感知無線環境工作中的關鍵技術之一[2-3]。頻譜分析是一個發展相對成熟的數字信號處理技術，它已經形成了許多具有特色的理論和算法。在認知無線電技術中，也可利用已有的算法進行無線環境檢測。

1 信任度函數

在認知無線電系統中，假設有多個認知用戶，且第i個和第 j個認知用戶測得的數據分別為 xi和 xj，若xi的真實性越高，則認為xi被其他數據所信任的程度就越高[2-3]。 所謂 xi被 xj信任程度，即從 xj來看 xi為真實數據的可能性，這種可能性被稱為信任度。為了對測得的數據間的信任度進行統一量化處理，通常定義一個信任度函數f來表示xi被xj信任的程度。根據信任度定義，設：

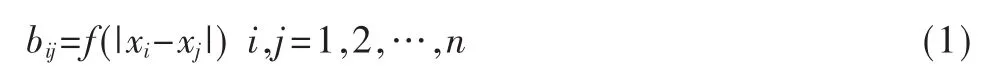
式(1)中，f為一個連續的下降函數，且 0≤f≤1,則信任度函數可表示為：

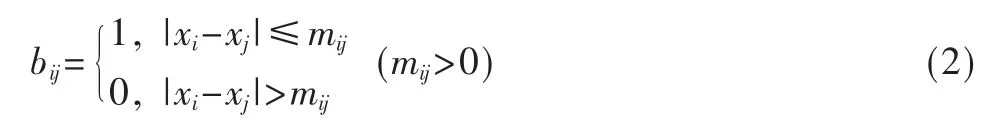
式(2)中，mij為融合上限。根據信任度數f的定義，可將其表示為指數函數的形式：

式(3)中|xi-xj|的值越小，bij的值就越大，數據 xi和 xj間的相互信任度就越大。當|xi-xj|的值為0時，bij=1。反之，如果|xi-xj|的值很大，則bij的值很小，說明數據 xi和 xj間的相互信任度bij很小。

由于指數函數 bij在|xi-xj|∈[0,∞]上的取值是 1～0單調遞減的，所以滿足了信任度函數應該具有的性質。在實際應用中,當|xi-xj|的值超過了設定的上限值mij時，可認為這兩個數據已經不再相互信任，此時bij=0。即：

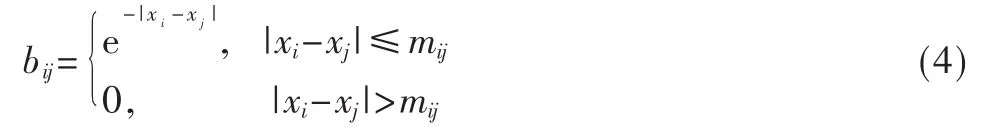
式(4)中，bij為滿足模糊性要求的指數函數形式。它既充分利用了模糊理論中信任度函數確定的優點，同時也避免了數據之間相互信任程度的絕對化，更加符合實際問題的真實性，可使融合結果更加精確和穩定。

假設有n個認知用戶，根據測得數據間的信任度函數bij，可建立信任度矩陣 B。

對于 B中第i行元素來說，若Σbij(j=1,2,…,n)的值較大，則表明第i個認知用戶測得的數據被大多數認知用戶信任。反之，信任度較小，即第i個認知用戶測得數據為真實數據的可能性較小。

2 數據融合

假設用wi來表示第 i個認知用戶測得的數據 xi在融合過程中所占的權重[4]。由于wi值的大小反映了其他認知用戶測得的數據對第i個認知用戶測得數據xi的綜合信任程度，因此可以利用wi對 xi進行加權求和，得到數據融合的表達式：

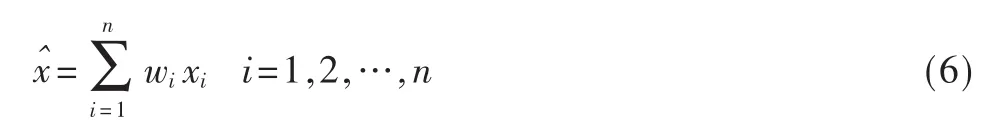
式(6)中，wi應滿足

wi綜合了一個關于xi的信任度系統中各子系統bi1,bi2,…,bin的全部信息，因此只需求出一組非負數a1,a2,…,an,使得：

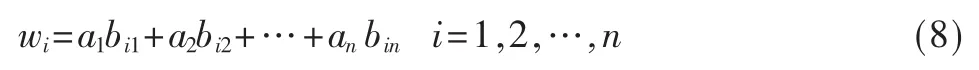
可以將式(7)改寫成矩陣形式：

式(9)中,W=[w1,w2,…,wn]T,A=[a1,a2,…,an]T。

由bij≥0可知信任度矩陣B是一個非負矩陣，且該對稱矩陣存在最大模的特征值 λ(λ＞0)，使得

可以求出λ及其對應的特征向量A，且A中的分量滿足 ai＞0(i=1,2,…n)的條件。 由此可得：

式(11)可作為對各認知用戶測得的數據間綜合信任程度的度量，即：

對wi進行歸一化處理，得到：

因此可求出對所有認知用戶測得的數據融合估計的最終結果為：

3 信任度函數在頻譜感知中的應用

3.1 頻譜感知的基本步驟

基于信任度函數的頻譜感知算法是在原來的能量頻譜感知算法的基礎上提出來的[5-6]，該算法針對未知信號模型，對于各認知用戶首先分別采用能量感知算法，然后對感知能量進行歸一化處理，再由融合中心確定信任度[7-9]。頻譜感知的流程圖如圖1所示。

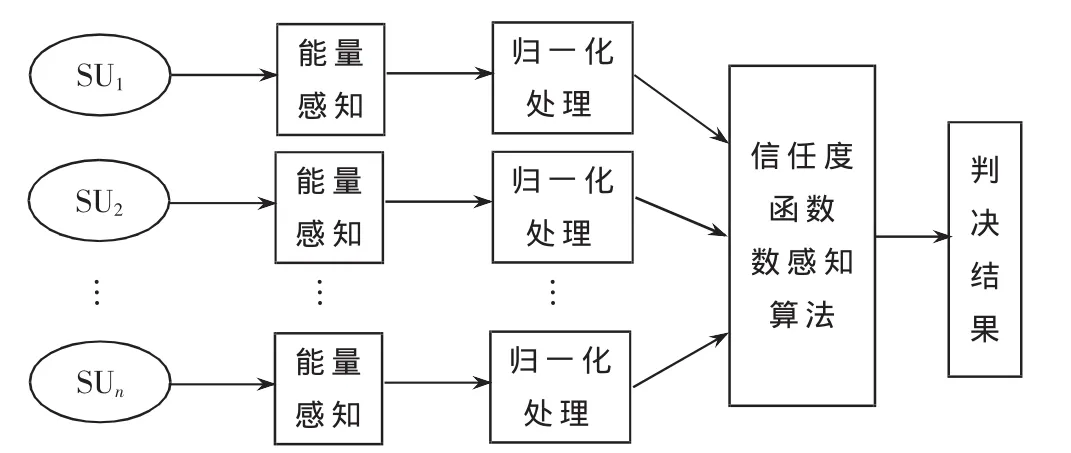
圖1 基于信任度函數頻譜感知流程圖

3.2 仿真及分析

假設具體仿真條件為：5 km×5 km的方形認知無線電網絡，單個認知用戶SU(Second User)的感知半徑RD為500 m。

假設認知用戶SU1～SU9在不同時刻利用能量感知算法對主用戶是否存在進行多次感知。再將各認知用戶的能量統計量歸一化處理得到14組數據如表1所示。其中，各認知用戶的判決結果取值范圍為0～1(若取值接近0則表示主用戶信號不存在，接近1則表示主用戶信號存在，判決結果在0.5附近時不確定性最大)。

經過多次檢驗，取 mij=0.2。 當|xi-xj|＞0.2時，bij=0；當|xi-xj|≤0.2時，對一般信任度函數來說 bij=1；對指數信任度函數來說bij=e-|xi-xj|。利用本文提出的方法對14組數據(可看作是14個時刻的檢測值)分別進行計算，其中以第2組數據為例，建立信任度矩陣，由矩陣計算得T2時刻一般信任度矩陣和指數信任度矩陣的最大模特征值 λ02、λ′02以及其對應特征向量 B02、B′02(即各信任度所占的權重)分別為：

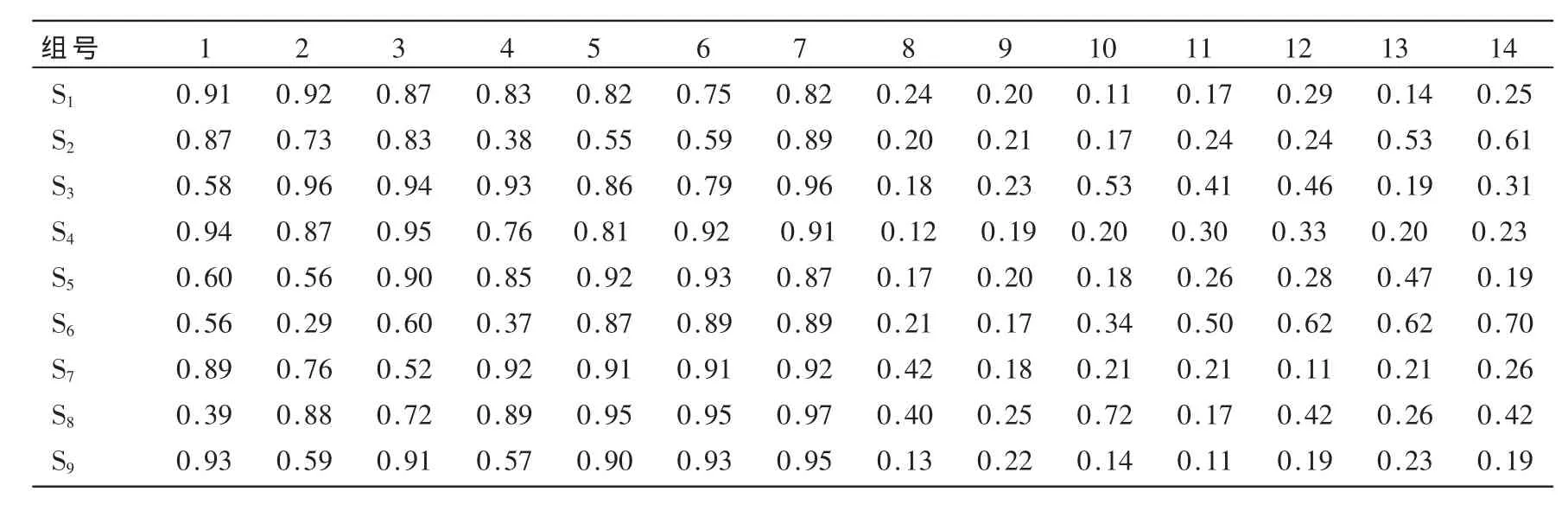
表1 各認知用戶在不同時刻感知信道的利用情況

單從數學的角度來看信任度函數的表達式，一般信任度函數的取值只有0和1兩種結果，而指數信任度函數是從0到1變化的[10]。因此，如果用一般信任度函數來處理不確定的信息，可能就會因為主觀判斷過于絕對化從而會出現錯誤的判斷結果。而對于指數信任度函數來說，當數據較多時可以近似為一個逐漸遞減的函數，對不確定信息的判斷不會過于絕對化。

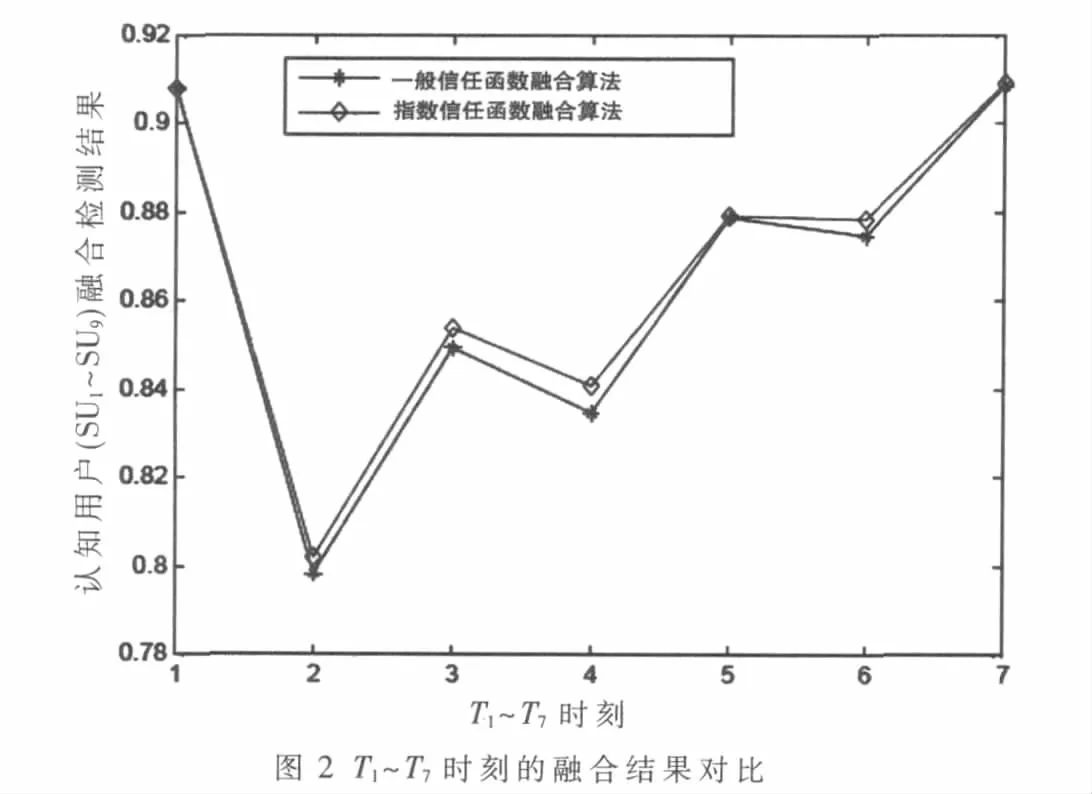
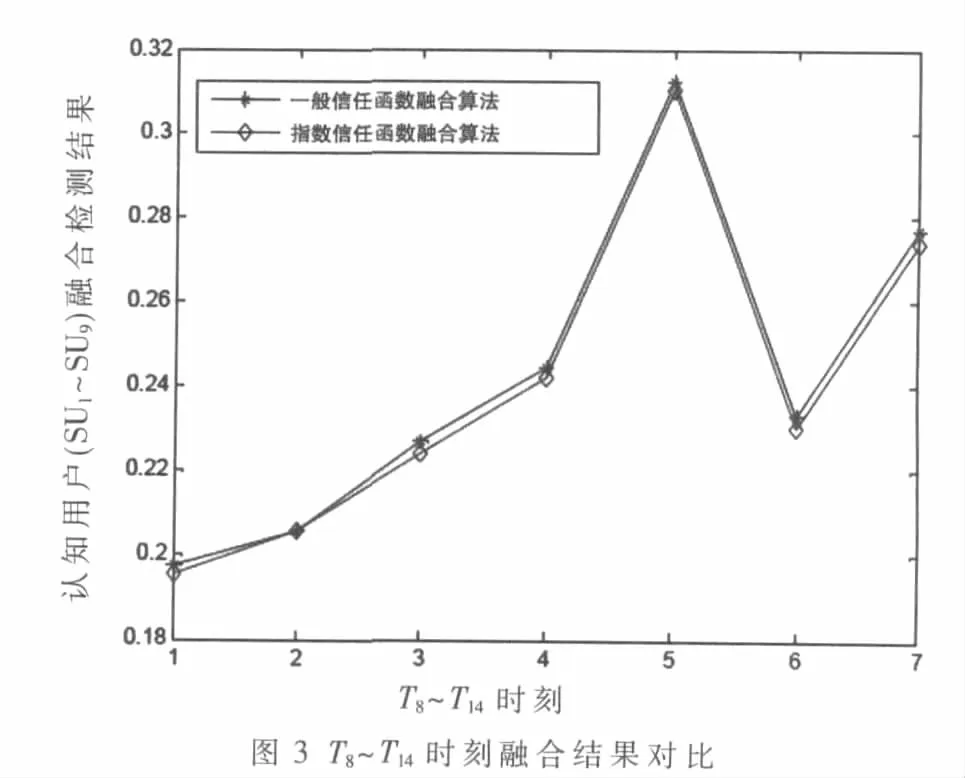
由圖2和圖3可知，在T1～T7時刻時，指數信任度函數的值大于一般信任度函數的值，在 T8～T14時刻，指數信任度函數的值小于一般信任度函數的值。這就說明若信任度較高，則指數函數的信任度大于一般函數的信任度；若信任度較低，則指數函數得出的信任度小于一般函數的信任度，即指數函數得出的信任度更接近實際的信任度。

對于融合結果來說，若授權用戶存在，則融合結果越大越好；反之，融合結果越小越好。例如在T2時刻時，授權用戶存在，采用指數信任度函數法和一般信任度函數法得到的融合結果分別為0.801 7和0.798 4。在T8時刻時，授權用戶不存在，采用指數信任度函數法和一般信任度函數法得到的融合結果分別為0.195 3和 0.197 4。即采用指數信任度函數法得到的結果更可靠。若某一認知用戶的信任度在0.5附近，則它的模糊性很高，但我們希望得到的融合結果能降低這種模糊性。由上述結果可知指數信任度函數法能滿足上述要求。

基于信任度函數的認知無線電頻譜感算法是考慮不同認知用戶和主用戶之間的信道環境以及各個用戶的感知可靠度的一種算法。采用一般信任度函數時，在可信度范圍內認知用戶的測量結果就會被完全信任。這樣不利于對實際情況做出客觀判別，從而導致融合結果受主觀因素的影響較大。若使用指數信任度函數，則能滿足信任度函數應該具有的特性，使得融合結果更加準確，具有更高的參考價值。由實際應用結果可知，采用指數信任度函數法得到的最終數據融合結果比一般信任度函數法得到的結果更加精確，并使數據融合過程具有更好的抗干擾性。

[1]吳今培,孫德山.現代數據分析[M].北京：機械工業出版社,2006.

[2]周賢偉,王建萍,王春江.認知無線電[M].北京：國防工業出版社,2008.

[3]馮文江,郭瑜,胡志遠.認知無線電中的頻譜感知技術[J].重慶大學學報(自然科學版),2007，30(11)：46-49.

[4]焦竹青，熊偉麗，張林，等.基于信任度的多傳感器數據融合及其應用[J].東南大學學報，2008,38增刊(1)：253-257.

[5]林威,吳捷,張欽宇,等.基于認知無線電系統合作檢測的數據融合研究[J].通信學報，2009(10)：135-140.

[6]卞荔，朱琦．基于數據融合的協作頻譜感知算法[J]．南京郵電大學學報(自然科學版),2009，29(2)：73-78.

[7]楊志偉,楊家瑋.認知無線電中的一種干擾溫度估計算法[J].通信技術,2006,39(12)：128-130.

[8]SAHAI A,HOVEN N,TANDRA R.Some fundamental limits in cognitive radio[C].Allerton Conf.on commun[C].Control and Computing 2004,October,2004.

[9]殷振華,耿志,劉郁林,等.基于能量檢測的頻譜感知方法的介紹[J].通信技術,2007,40(11)：83-85.

[10]胡振濤,劉先省.基于相對距離的一種多傳感器數據融合方法[J].系統工程與電子技術,2006,28(2)：196-198.