基于雙核Nios II系統(tǒng)的數(shù)字預(yù)失真器設(shè)計*

曾德軍，石棟元，李金政，夏 威，何子述

（電子科技大學(xué) 電子工程學(xué)院，四川 成都611731）

在現(xiàn)代無線通信系統(tǒng)中，功率放大器（PA）是整個發(fā)射機中最為關(guān)鍵的部件之一。然而，PA固有的非線性特性會對通信質(zhì)量造成嚴重影響。數(shù)字預(yù)失真技術(shù)作為一種高效的功放線性化方法，近年來得到了廣泛重視和研究[1-4]。

傳統(tǒng)的數(shù)字預(yù)失真器一般采用FPGA+DSP的方案，結(jié)構(gòu)較為復(fù)雜，成本較高。本文在FPGA芯片中構(gòu)建了SoPC系統(tǒng)，設(shè)計了一個自適應(yīng)數(shù)字預(yù)失真器（DPD），它具有集成度高、成本低等優(yōu)點。同時，采用并行RLS算法提取DPD模型參數(shù)，降低了傳統(tǒng)RLS預(yù)失真算法的復(fù)雜度。采用雙核Nios II并行操作，提升了硬件處理速度，保證了預(yù)失真處理的實時性和敏捷性。

1 DPD多查找結(jié)構(gòu)

本文采用記憶多項式模型[5]作為DPD的行為模型，表示為：

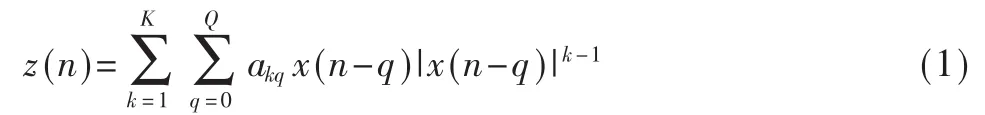
其中，x(n)和z(n)分別代表DPD的輸入和輸出信號，akq為記憶多項式模型參數(shù)，K為多項式階數(shù)，Q為記憶深度。

實現(xiàn)式(1)的方法是將其表達成基本預(yù)失真單元(BPC)的組合形式，如圖1所示。其中，表項值函數(shù)的表達式如下：

本文使用間接學(xué)習(xí)結(jié)構(gòu)[6]提取DPD的參數(shù) akq，通過參考文獻[6-7]的推導(dǎo)可知，參數(shù)提取方程總可以轉(zhuǎn)換成如下形式：

其中，a=[a10，…，aK0，…，a1Q，…，aKQ]T為 DPD 參數(shù)向量；U=[u10，…，uK0，…，u1Q，…，uKQ]為與輸入信號有關(guān)的輸入矩陣；z為與期望信號有關(guān)的向量。考慮到參數(shù)計算數(shù)值穩(wěn)定性問題和DPD對突變環(huán)境的適應(yīng)能力，工程上一般采用自適應(yīng)算法求解式(3)。

2 并行RLS算法及其Nios II實現(xiàn)

RLS算法作為一種應(yīng)用極為廣泛的自適應(yīng)算法，具有性能優(yōu)越、收斂速度快等優(yōu)點。然而，傳統(tǒng)的RLS算法涉及到大量的高維矩陣操作，算法復(fù)雜度高。本文根據(jù)參考文獻[8]的思想，對傳統(tǒng)RLS算法進行改進，生成并行RLS算法，并將其運用到DPD模型的參數(shù)提取過程中。

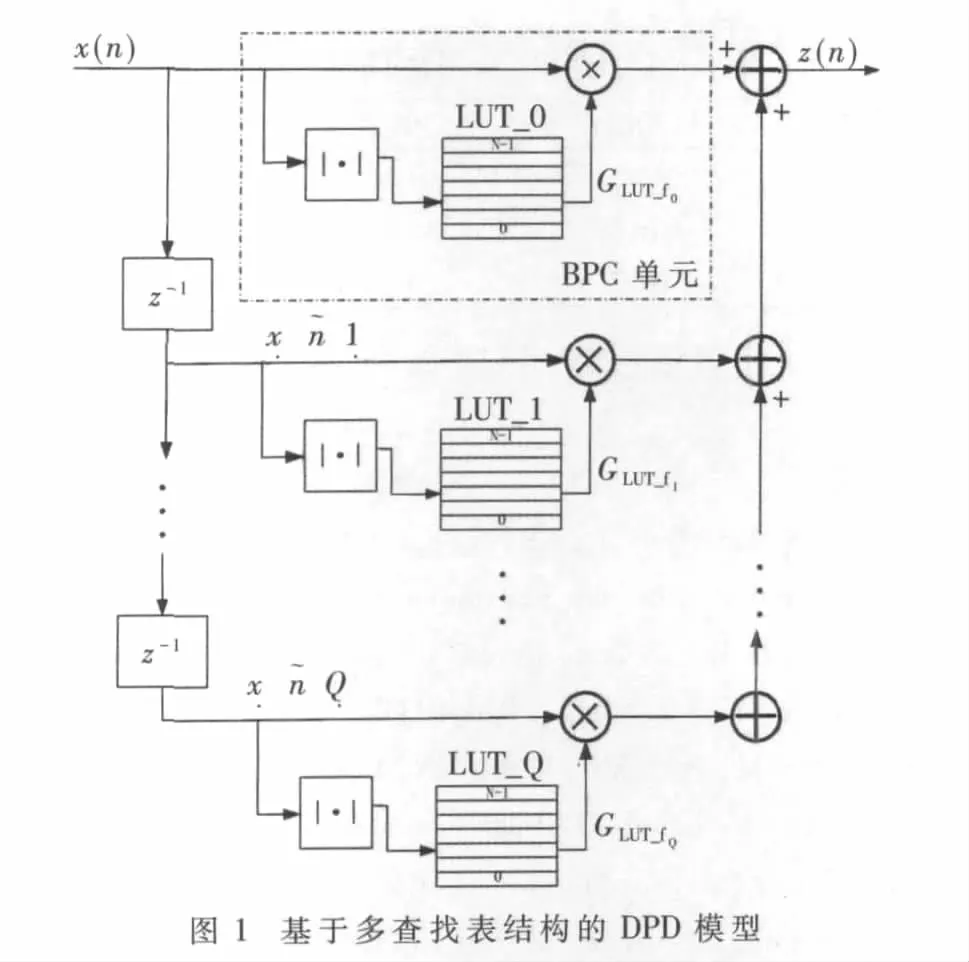
并行RLS算法的核心思想是將n時刻矩陣U的向量元素 u(n)以及 DPD參數(shù)向量 a(n)劃分為 q組子向量，分別為 ui(n)、ai(n)，其中 i=1，2，…，q，進而生成子濾波器組。采用自適應(yīng)算法對各組子濾波器分別更新，更新完成后再將各子濾波器的權(quán)向量重新組合成一個完整的權(quán)向量，即aopt(n)。并行 RLS算法的步驟如表1所示。已知條件為：新輸入向量u(n)，權(quán)向量 a(n-1)，期望信號 d(n)，矩陣 P(n-1)。

表1 并行RLS算法步驟

表2對比了傳統(tǒng)RLS算法與并行RLS算法在加法和乘法運算量上的差異。相對于傳統(tǒng)RLS算法，并行RLS算法的最大優(yōu)勢在于降低了矩陣維數(shù)，故減小了運算復(fù)雜度。

從表2可知，并行RLS算法的q值越大，算法復(fù)雜度的優(yōu)化程度越高。然而，多次仿真實驗證明隨著q值的增加，并行RLS算法的收斂速度會變慢，性能也會受到影響。經(jīng)過綜合權(quán)衡后，本文使用q=2時的并行RLS算法，并采用雙核Nios II進行實現(xiàn)，其架構(gòu)如圖2所示。

表2 傳統(tǒng)RLS與并行RLS算法的運算量

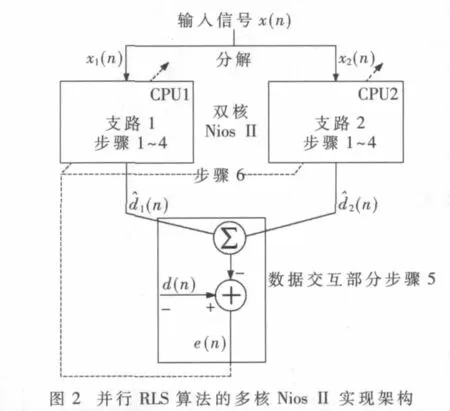
在并行RLS算法中，主要的濾波過程和算法更新過程都是完全獨立的，可以在CPU1和CPU2中并發(fā)執(zhí)行。并行RLS算法涉及到的交互數(shù)據(jù)放在共享存儲區(qū)內(nèi)，雙核可以通過互斥機制訪問。

圖3為基于查找表的DPD在雙核Nios II系統(tǒng)中的實現(xiàn)結(jié)構(gòu)。該系統(tǒng)的工作狀態(tài)可以經(jīng)歷如下階段：

(1)DPD學(xué)習(xí)過程：DPD不加入傳輸鏈路，基帶信號直接上變頻后輸送至PA，雙核Nios II收集基帶信號和PA反饋信號。

(2)并行RLS算法處理過程：雙核Nios II按照圖2的步驟求解出DPD模型參數(shù)向量a。

(3)查找表更新過程：將a的元素值代入方程式，通過雙核Nios II計算出查找表的表項值，并將表項值寫入查找表RAM中，完成更新。

(4)DPD工作過程：DPD加入傳輸鏈路，構(gòu)成DPD+PA的完整預(yù)失真系統(tǒng)。基帶信號通過查表完成預(yù)失真操作。

3 系統(tǒng)功能驗證

本實驗中采用的功放的中心頻率為710 MHz，線性增益為43 dB，1 dB壓縮點為-8.5 dBm；DPD模型的多項式階數(shù)為3，記憶深度為2，輸入到PA的測試信號是具有5 MHz帶寬的WCDMA信號。

通過圖4和表3可見，WCDMA信號在未加入DPD前，其鄰道頻譜干擾嚴重，ACPR只有19 dB。但加入DPD后，信號的帶外雜散信號得到抑制，且ACPR改善量在15 dB～20 dB之間。同時，加入DPD后系統(tǒng)的NMSE得到明顯改善，WCDMA信號帶內(nèi)失真得到了控制。實驗測試表明，DPD的預(yù)失真效果理想，達到了預(yù)期設(shè)計目的。

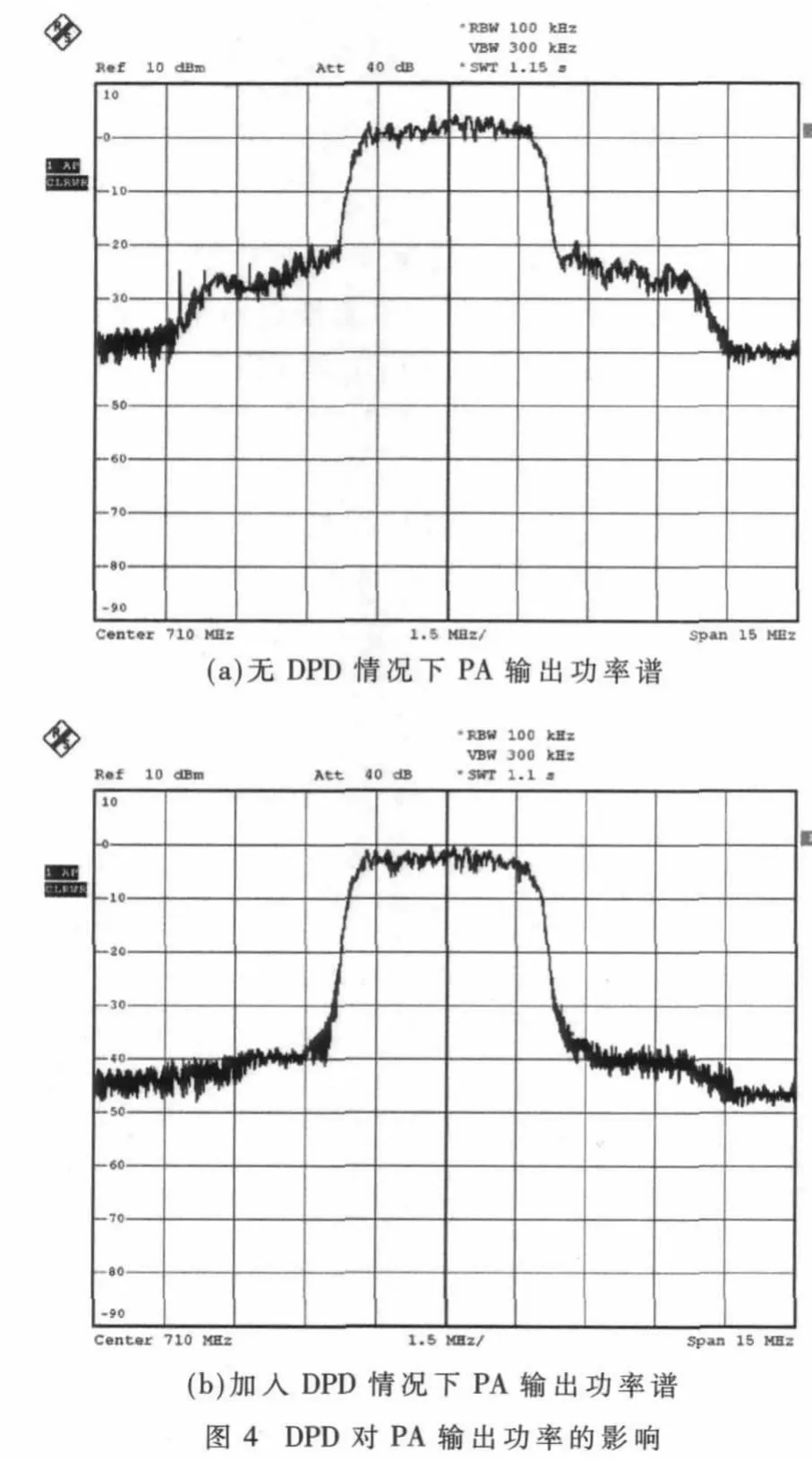
本設(shè)計在FPGA芯片中實現(xiàn)了一個基于雙核Nios II的自適應(yīng)數(shù)字預(yù)失真器（DPD）。該系統(tǒng)穩(wěn)定可靠，能夠?qū)Ψ诺姆蔷€性進行較好的補償，且能夠抑制信號經(jīng)過功放后的帶外頻譜滋生，同時提高了信號在帶內(nèi)頻譜的平坦度。

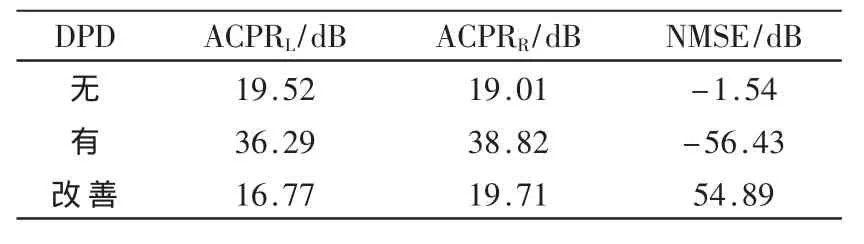
表3 WCDMA信號下DPD系統(tǒng)實測性能

[1]HONG S，WOO Y Y，KIN J，et al.Weighted polynomial digital predistortion for low memory effect doherty power amplifier[J].IEEE Transaltions on Microwave Theory and Techniques，2007，55(5)：925-931.

[2]YOUNES M，HAMMI O，KWAN A，et al.An accurate complexity-reduced “PLUME”model for behavioral modeling and digital predistortion of RF power amplifiers[J].IEEE Transactions on Industrial Electronics，2011，58(4)：1397-1405.

[3]GUAN L，ZHU A.Dual-loop model extraction for digital predistortion of wideband RF power amplifiers[J].IEEE Microwave and Wireless Components Letters，2011，21(9)：501-503.

[4]GILABERT P，MONTORO G，BERTRAN E.FPGA implementation of a real-time NARMA-based digital adaptive predistorter[J].IEEE Transactions Ciruits And System，2011，58(7)：402-406.

[5]DING L，ZHOU G T，MORGAN D R.A robust digital baseband predistorter constructed using memory polynomials[J].IEEE Transactions on Communication，2004，52(1):159-165.

[6]劉寧.功放數(shù)字預(yù)失真算法研究及硬件實現(xiàn)[D].成都：電子科技大學(xué)，2011.

[7]GILABERT P L，CESARI A，MONTORO G，et al.Multilookup table FPGA implementation of an adaptive digital predistorter for linearizing RF power amplifiers with memory effects[J].IEEE Transaction on Microwave Theory and Technigues，2008，56(2)：372-384.

[8]CHATURVEDI A K，SHARMA G.A new family of concurrent algorithms for adaptive volterra and linear filters[J].IEEE Transactions on Signal Processing，1999，47(9)：2547-2551.