快速傅里葉變換的硬件實現

蘭海洋，林曉煥

（西安工程大學 電子信息學院，陜西 西安 710048）

0 引言

19世紀20年代，法國工程師傅里葉（Fourier）指出：任意一個周期函數都可以分解為無窮多個不同頻率正弦信號的和，這即是傅里葉級數[1]，求解傅里葉系數的過程就是傅里葉變換。傅里葉變換的應用非常廣泛，主要的領域有：物理學、電子類學科、數論、組合數學、信號處理、概率論、統計學、密碼學、聲學、光學、海洋學、結構動力學等[2]。快速傅里葉變換（FFT）是離散傅里葉變換（DFT）的一種快速算法。一般采用 ROM 的方法來實現FFT，其速度不能滿足實時性的要求[3]，這里采用移位存儲器的方法來存儲旋轉因子，大大地提高了FFT的運算速度。

1 算法原理

設長度為N的有限序列x(n)的DFT為：

設序列x(n)的長度N(N=2M,M為任意整數)按N的奇偶性把x(n)分解為兩個N/2點的子序列：

則x(n)的N點DFT為：

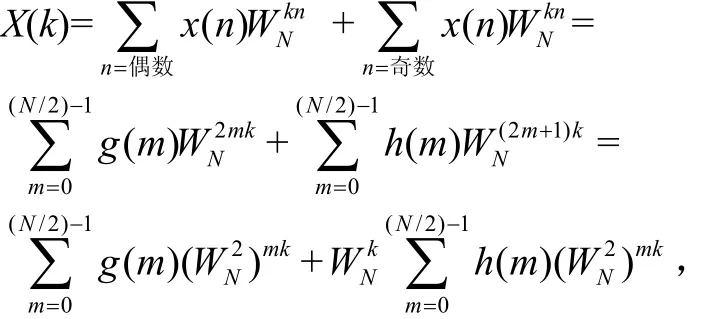
由于

所以

式中，G(k)和H(k)分別為 g(m)和 h(m)的 N/2點 DFT，表達式如下：

由于G(k)和H(k)均以N/2為周期，考慮到對稱性，有,X(k)就可表達式為：

這樣就將N點的DFT分解為兩個N/2點的DFT以及上面兩式的運算，使DFT運算量減少，將每個N/2點的DFT分解為兩個N/4點的DFT，由于N是2 的正整數次冪，還可以繼續分下去，直到分解為2點的DFT為止，這種運算可用圖1的流圖表示，稱為蝶形運算符。當N=8時[5]，整個信號的流圖如圖2所示。

圖1 蝶形運算符

圖2 8點FFT蝶形運算示意

2 電路過程原理

2.1 FFT的總體設計

FFT設計主要由以下部分組成：蝶形運算單元，地址產生單元，功能切換單元，存儲單元，浮點單元和時序控制元。各模塊功能如下：

蝶形運算單元采用DIT方式完成FFT的蝶形運算，雙口RAM1和 RAM2作為存儲器，從RAM1中讀出數據存入RAM2中，或從RAM2中讀出數據存入RAM1中。ROM作為預置旋轉因子的存儲單元，功能切換單元用來完成RAM1與RAM2間數據讀寫功能的切換；地址產生單元用于產生 RAM 的讀、寫地址和 ROM 的讀地址；浮點單元用于記錄蝶算單元輸出數據的位信息并完成蝶算單元輸入數據的截位；時序控制單元：產生各模塊的使能信號、控制信號，使整個流程正常有序的工作。

2.2 蝶形單元的設計

由以上分析可知，蝶形運算單元是FFT算法最核心的的部分。因此要實現FFT算法電路，首先是設計蝶形運算單元，然后利用蝶形模塊及其他幾個模塊的配合實現FFT。

由圖1可知，蝶形模塊的輸出為A+BC和A-BC。這里涉及加法、減法、和乘法的相互運算，即蝶形運算單元的電路主要由加法器、減法器和乘法器構成[5]。

1）N為加法器。多為加法器的構成有兩種方式：串行進位和并行進位。串行進位方式是將全加器級聯構成多為加法器。并行進位加法設有并行進位產生邏輯，運算速度快；并行進位加法器通常比串行級聯加法器占用的資源多。隨著位數的增加相同位數的并行加法器與串行加法器的資源占用快速增大。蝶形運算模塊中采用并行進位的實現方式[6]。

2）N位乘法器。N位乘法器的運算方法和手工算法一樣，是由N位加法器構成的以時序邏輯方式設計的N×N位乘法器方案，其原理是：若被乘數某位為 1，則乘數左移幾位，若為 0則不進行運算，然后逐次相加，直至被乘數的最高位[7-8]。

3）N位減法器。其設計方法和原理和加法器相同。

以輸入信號為8為二進制數來實現FFT設計，具體說明如何利用Verilog HDL語言完成蝶形運算單元的設計與實現。圖3為蝶形運算單元的核心電路圖，蝶形運算的實現由乘法器、加法器和減法器和控制輸出使能模塊相互運算完成的。

圖3 蝶形運算單元的核心電路

其中X1_r，X1_im，X2_r，X2_im分別為X1，X2的實部與虛部，c,d分別代表復數的實部與虛部；y1_r,y2_r,y1_im,y2_im分別代表輸出y1,y2的實部與虛部，他們分辨對應于A+BC和A-BC的實部與虛部。圖4為蝶形運算單元模塊。

圖4 蝶形運算單元模塊

3 實驗結果

在XILinxA公司的FPGA上進行驗證，目標芯片采用Virtex系列的XCV300，編寫軟件為ISE 10.1。

Virtex是Xilinx FPGA中的高端產品，內部有豐富的資源，包括RAM，乘法器，IOB，可編程互聯線，數字時鐘管理器 DCM 和可編程邏輯陣列CLB，這一系列產品不斷的升級和更新，性能也越來越卓越。 FFT的仿真圖如圖5所示。由波形圖5中可以看出，當Start為低電平時，FFT開始運算，給輸入端順序送入8個數據，計算結束后，數據從輸出端順序輸出。大大提高了運算速度。

圖5 FFT運算仿真波形

4 結語

文中采用Verilog語言實現FFT算法，利用ISE進行仿真，在分析快速傅里葉變換（FFT）算法的基礎上[9-10]，采用移位存儲器存儲算子的方法，提高了運算速度，滿足了實時性的要求。采用FPGA實現高速數字信號處理的算法具有可行性和優越性，由于FPGA的并行性特點使得算法的實現速度具有很大的提升，因此越來越得到電子工程師們的青睞，但由于文中采用256點基2FFT算法，使數據和性能方面存在缺陷，可以采用1024點FFT提高性能和數據精度。

[1] 王遠模,趙宏鐘.用FPGA實現浮點FFT處理器的研究[J].國防科技大學學報，2004，26(06):61-64.

[2] 李加元,成立.系統芯片設計的可復用護技術[J].半導體技術，2006，32(0l):15-19.

[3] 劉歡,謝志遠.分裂基 FFT算法討論與改進[J].通信技術，2008，41(03):124-128.

[4] 劉韜,樓興華.FPGA數字電子系統與開發實例導航[M].北京:人民郵電出版社，2005.

[5] 韓穎,王旭,吳嗣亮.FPGA實現高速FFT處理器的設計[J].電訊技術，2003(02):74-78.

[6] 劉韜,樓興華.FPGA數字電子系統與開發實例導航[M].北京:人民郵電出版社，2005.

[7] 袁俊全,孫敏琪,曹瑞.Verilog HDL數字系統設計及其應用[M].西安:西安電子科技大學出版社，2002.

[8] 李懷金,王大鳴.數字匹配濾波捕獲方法研究與 FPGA實現[J].通信技術，2007,40(05):41-43.

[9] 姚興波,楊永俠.FFT算法在 OFDM中的應用研究與設計[J]. 信息安全與通信保密,2011(03):58-60.

[10] 李勇,李雀.OFDM系統中多導頻的FFT信道估計算法[J].信息安全與通信保密,2008(03):30-33.