深空通信中極低碼率編碼技術研究

岳 平，胡 飛

（西南通信研究所，四川 成都 610041）

0 引言

深空通信的特點是通信距離長、信號衰減大以及地面信噪環境惡劣，這樣較難進行信號處理。構造逼近香農極限的信道糾錯編碼且能在深空環境中得到應用是深空通信研究中的一項重要內容，糾錯編碼能有效地提高系統的利用效率。一直以來，深空通信將級聯碼作為信道編碼技術，傳統方式是將卷積碼作為內碼，RS碼作為外碼。由于深空通信的發展，傳統編碼技術已經難以滿足需求，同時，碼率較低，碼長較長的碼字的設計得以實現，可以將其應用到深空通信。

1977年，Paul D. Shaft首先研究了用于擴頻通信的低碼率（碼率1/2到1/64）卷積碼。1990年，A. J. Viterbi提出了一類由Hadamard碼卷積級聯構造的低碼率正交卷積碼（碼率低至 1/512）。基于Turbo碼的思想，1997年又提出了低碼率的串接Hadamard碼，其后Ping L等提出了低碼率的Turbo-Hadamard碼[1]，其碼率為7/370，誤碼率為510-時，可達到-1.2 dB，但存在誤碼平臺。

繼Gallager在1962年提出了低密度奇偶校驗碼（LDPC）后，Tanner于1981年提出了廣義低密度奇偶校驗碼（GLDPC）的概念[2-3]。最近Yue Guosen和Ping L等基于 LDPC碼的思想提出了 LDPC-Hadamard碼[4]，距-1.6 dB的距離更近，LDPC碼沒有誤碼平臺，LDPC- Hadamard碼也是沒有誤碼平臺的。

文獻[4]描述了 LDPC-Hadamard 碼的構造原理，并提出了優化方法。為了將其應用到深空通信系統中，本文基于文獻[4]的設計思想設計出了一種低碼率的LDPC-Hadamard 碼。

本文首先給出了 LDPC-Hadamard碼的基本構造模型并分析了譯碼過程；列出了LDPC-Hadamard碼基本模型的不足，接著改進和構造了低碼率的碼字并進行仿真，分析了碼率和碼長，研究了它們對碼字性能的影響；最后是全文總結。

1 LDPC-Hadamard碼

1.1 LDPC-Hadamard編碼結構

構造 LDPC[5]碼實際上就是對校驗矩陣進行設計。在校驗矩陣H中，每行表示一個約束方程，每列表示一個符號變量，Tanner圖中分別用校驗節點和變量節點表示。如果校驗矩陣中的任意一個元素= 1，則表示第i個校驗節點與第j個變量節點相連，否則不相連。度為j的變量節點是一個( j ,1)的重復碼，度為j的校驗節點是一個(j, j - 1 )的單奇偶校驗碼。

將LDPC碼的校驗節點由單奇偶校驗碼約束換成其它分組碼約束，就構成了GLDPC碼[6]，如果將單奇偶校驗碼約束換成 Hadamard碼約束則構成了LDPC-Hadamad碼。

1.2 LDPC-Hadamard譯碼方法

因子圖用來描述一個全局函數的乘積因子和變量之間的關系。一個因子圖包含有兩類節點，分別是函數節點jf和變量節點iυ。若iυ是jf的自變量，那兩點連一條線。SP算法使消息在因子圖上傳遞，來計算某個變量的邊緣函數。符號表示從節點υi傳給節點fj的消息，符號表示節點jf傳給節點iυ的消息。SP算法消息更新的規則為：

其中 n (q)表示因子圖與節點q相連的節點集合，υQj表示與第j個因子有關的變量集合。邊緣函數即為進入每個變量節點的消息之積。

Tanner圖是一種特殊的因子圖，用 SP算法對LDPC碼和LDPC-Hadamard碼進行迭代譯碼。｛rk｝表示接收信號，表示第k個符號從AWGN信道得到的消息；表示與第k個變量節點相連的邊的集合，Um與第m個校驗節點相連的邊的集合；rm,k表示第m個校驗節點傳給第k個變量節點的外部消息，表示第k個變量節點傳給第m個校驗節點的外部消息； qk表示比特的后驗對數似然比，而表示判決后得到的碼字，其中的 LDPC碼字由表示，H表示 LDPC碼的校驗矩陣；r表示Hadamard的階數，H-1表示Hadamard碼譯碼器。譯碼算法如下：

（1）初始化

（2）迭代

1）水平步驟：

2）譯碼：

3）垂直步驟：

1.3 LDPC-Hadamard存在問題分析

GLDPC的碼率可以由公式得出：

所以：

其中，cR是校驗節點的平均碼率。設0＜R＜1，如果有多余的碼作為重復碼字，當cR小于1/2時，碼字中包含有不可忽略的度1節點。

前面提到的LDPC-Hadamard碼存在較多度為1的變量節點，且其數目與 Hadamard碼的階數r（ 3r≥ ）成正比。進行迭代譯碼時，度為1的節點的外信息不會被更新，碼字性能會受到影響。

從文獻[4]可知，為了接近信道的最大容量，變量節點和校驗節點的 EXIT曲線必須相匹配。由于變量節點的EXIT曲線是凹形的，而Hadamard碼的EXIT曲線既不是凹形也不是凸形，因此，它們的EXIT圖不能被優化而相互匹配。

2 LDPC-Hadamard碼的改進和優化

[4]，對 LDPC-Hadamard碼設計一種新的編碼結構來解決上述問題。

如圖1所示：①通過PEG算法構造一個信息位為K，碼長為 NL，碼率R的規則 LDPC碼，行重為ρ，列重為λ；②將LDPC碼字中與校驗節點相連的所有變量比特映射成為階數 r =ρ-2的Hadamard碼并除去它的信息比特，得到 M = NL-K個Hadamard碼字，每個Hadamard碼字長為2r-ρ；③將LPDC碼字和這些Hadamard碼字組合在一起得到碼長為的LDPC-Hadamard碼，碼率。表1是各種碼率的編碼參數。

圖 1 LDPC-Hadamard碼的構造

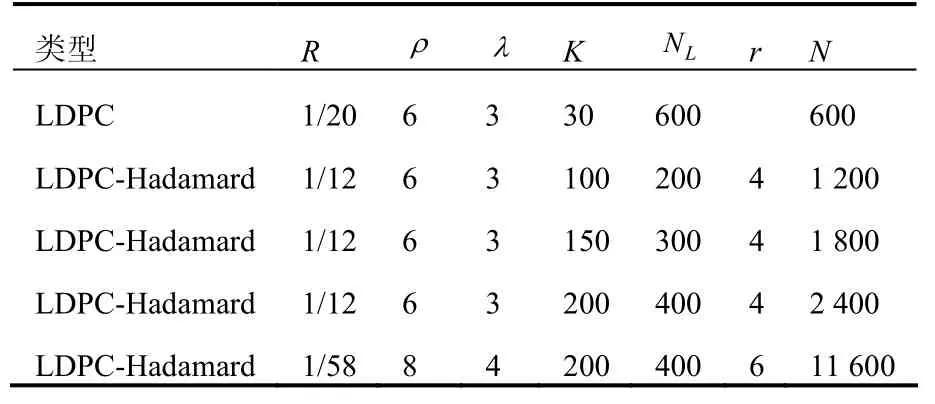
表1 LDPC碼及各種碼率的LDPC-Hadamard碼

3 仿真結果與分析

仿真分析了LDPC碼[7]和LDPC-Hadamard碼的誤碼性能，其中LDPC采用了文獻[5]提出的編碼方案，LDPC-Hadamard碼如表1所示，碼字長度分別為1 200和11 600。仿真結果如圖2所示。

由圖2知，LDPC-Hadamard碼性能比LDPC碼改善了 0.8 dB以上。對于兩種不同的 LDPCHadamard碼，碼長11600的LDPC-Hadamard碼的誤碼性能比碼長1200的LDPC-Hadamard誤碼性能更好，二者差距為0.4 dB，但是后者碼字長度短很多，便于工程實際應用。

圖2 不同碼率的碼字性能

圖3給出了表1中碼率為1/12、不同碼字長度的 LDPC-Hadamard碼的誤碼性能對比，這些LDPC-Hadamard編碼采用了相同的編碼方法。可以看出：LDPC-Hadamard碼字長度越長，其性能越好，大約改善了0.025 dB以上。但是，碼字過長將導致譯碼延時過大，不便于工程應用。

圖3 碼長對譯碼性能的影響

4 結語

GLDPC碼[8-9]基于傳統LDPC編碼技術，采用級聯編碼思想來構造新型編碼，其誤碼性能較好。LDPC-Hadamard碼是一種特殊的GLDPC碼，它將LDPC碼和 Hadamard碼級聯起來，其性能優于LDPC碼。仿真結果表明，LDPC-Hadamard碼在碼率為 1/58、碼字長度為 11600時，誤碼率為 1 0-5的信噪比可達到-0.7 dB，而碼率為1/12、碼字長度為1 200的LDPC-Hadamard碼在誤碼率為 1 0-5的信噪比可達到-0.2 dB。LDPC-Hadamard編解碼技術能夠在極低信噪比的深空通信等環境中得到廣泛應用。

參考文獻

[1] PING L, LEUNG W K,WU K Y.Low-rate Turbo-Hadamard Codes[J].IEEE Trans. Inf. Theory,2003(49):3213-3224.

[2] TANNER R M.A Recursive Approach to Low Complexity Codes[J].IEEE Transactions on Infromation Theory,1981,27(05):533-547.

[3] BOUTROS J, POTHIER O, ZEMOR G.Generalized Low Density (Tanner) Codes[C].USA:IEEE Press,1999:441-445.

[4] Yue Guosen, Li Ping,Wang Xiaodong. Generalized Low-density Parity-check Codes on based Hadamard Constraints[J]. IEEE Transactions on Information Theory,2007,53(03):1058-1079.

[5] 韓輝,周武旸,董桂強,等.一種改進的 LDPC碼譯碼算法[J].通信技術,2009,42(11):214-216.

[6] LENTMAIER M,ZIGANGIROV K S.On Generalized Low-density Parity-check Codes based on Hamming Component Codes[J]. Communication Letters,1999,3(08):248-250.

[7] 易燕,申敏.一種快速準規則 LDPC碼編碼器的硬件實現[J].信息安全與通信保密,2007(04):54-55.

[8] MILADINOVIC N,FOSSORIER M P C.Generalized LDPC Codes and Generalized Stopping Sets[J].IEEE Transactions on Communication,2008,56(02):201-212.

[9] 龔莉萍,陳云榕,胡凱.LDPC編譯碼技術研究[J].通信技術,2009,42(07):10-12.