改進小波在調制模式識別中的應用

秦立龍，王振宇，閆朋展

(解放軍電子工程學院信息系，安徽 合肥 230037）

0 引言

在調制模式自動識別的框架內，調制模式自動調制識別一般使用統計模式識別[1]。基于統計模式識別的方法可以分成兩個部分：特征提取和分類器設計。特征提取負責對接收到的信號提取出最能表現其調制特征的參數。分類器則根據已提取出的特征把信號劃分到相應的類別。現有的數字調制模式識別特征提取算法主要歸納為以下幾種：基于瞬時信息的特征提取、基于時頻分析的特征提取、基于累積量的特征提取、基于譜相關法的特征提取等。

針對通信信號調制模式的特點，提出了一種新的特征提取方法，將最優插值估計算法用于預測器的設計。經過仿真證明，這種基于最優插值估計的提升小波效果優秀，符合工程需要。

1 小波變換簡述

第2代小波變換[2]是Swelden提出的一種不依賴于傅里葉變換的小波構造方法，小波基構造方法靈活，算法簡單，執行效率高。第2代小波變換將傳統小波變換過程分為分裂、預測和更新3個階段。

（1）分裂

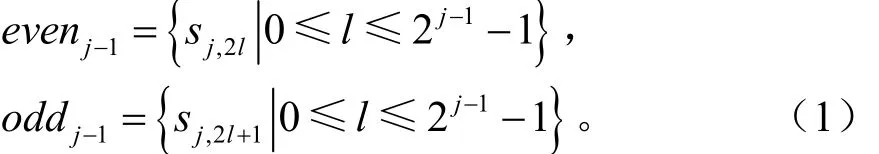
（2）預測

對于一個局部相關性較強的信號，它的偶子集和奇子集是高度相關的，因此，知道其中任何一個，就有可能在它合理的精度范圍內預測另一個。記預測算子為P，預測誤差 dj-1即為：

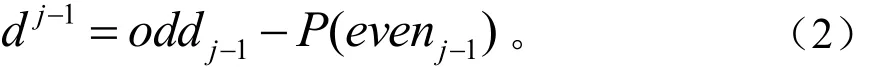
（3）更新

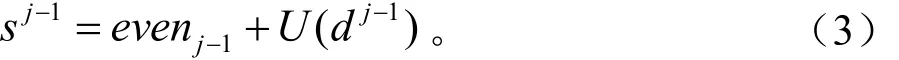
2 小波變換的改進

為了有效地提取分析信號的特征，使P的選擇能夠反映信號的結構，將最優估計方法[3]引入 P的設計，以期獲得一組最優的預測系數，即尋找一組P使目標函數J=dTd最小。使用相鄰的2D (D為正整數)個偶樣本來進行估計，設：

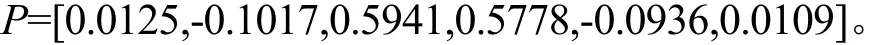
3 特征的提取

首先利用MATLAB產生了高斯白噪聲信道下7種待識別數字信號的仿真數據，這7種常用數字調制信號為：2ASK、4ASK、2FSK、8FSK、MSK、4PSK、8PSK、16QAM信號，主要調制參數為：載頻fc=10 kHz，采樣頻率fs=200 kHz，MSK碼元速率fb=4×fc/5，其他信號碼元速率為fb=2 000 B，頻率偏移量Δf =2 000 Hz。提取的特征參數定義如下：

三要大力培育農民用水戶協會等群管組織，建立完善村級水管員制度，使每一項農水工程都落實好管理主體。要建立和完善收費補償機制，實行政府補貼，通過業主招標、承包租賃等方式，保障投入農田水利設施資金的合理效益。

std(·)表示標準差算法，di為第 i層分解的細節系數。通常均值差別越大，類間分離越好；方差越小，類內聚集越好。對7種調制信號以間隔1 dB變化加入信噪比為0～20 dB的噪聲，每種特征參數各取150個特征樣本，計算特征參數的均值。以第三層特征分解為例，仿真結果如圖1所示。

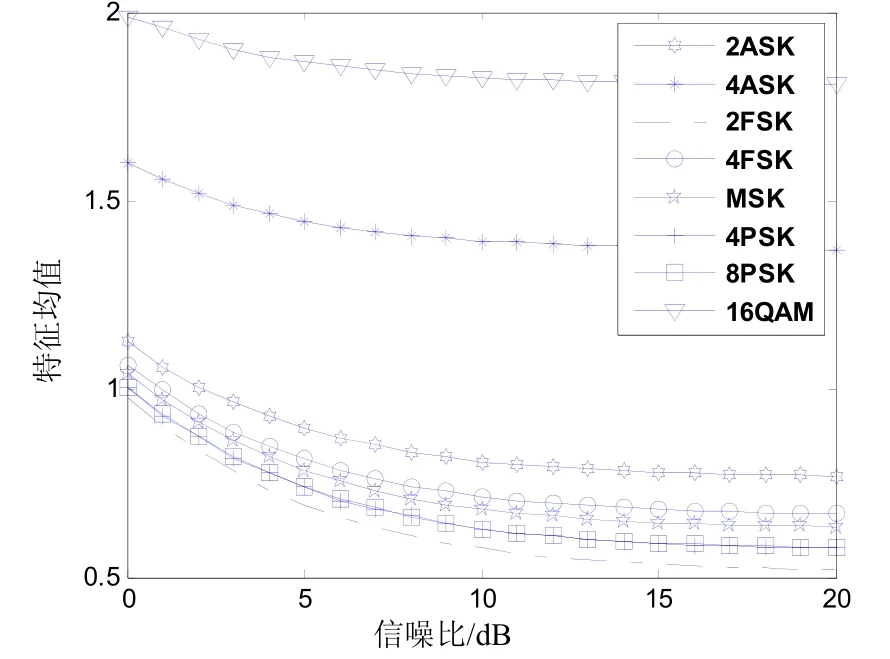
圖1 第三層分解數據的標準差隨信噪比變化曲線

由圖可得，不同調制方式的信號特征差別較大，所以提取的分類特征能實現其類間、類內識別。

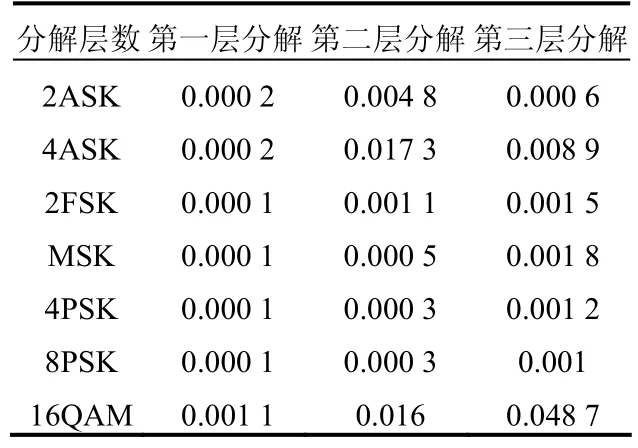
表1 信噪比為5 dB時歸一化特征參數均值的方差

通過表1可以看出，改進的第二代小波方差較小，表明算法得到的數據類內聚集較好。在此基礎上，可以進一步進行調制模式識別。

4 特征識別性能分析

4.1 分類器的設計

支持向量機（SVM，Support Vector Machine）是依據統計學習理論提出的一種機器學習方法[5]。它是以結構風險最小化準則來實現的，其魯棒性強，結構簡單、推廣性好，彌補了神經網絡分類器存在的固有問題，具有很大的優越性。分類器使用徑向基核函數[6]，其表達式為：

分類器的結構采用二叉樹支持向量機。由于類距離算法在分類問題中性能優良，并且推廣性能好，所以依據該算法生成二叉樹結構。經計算機仿真確定的二叉樹分類向量機結構為：16QAM、4ASK、2ASK、2FSK、MSK、4FSK、4PSK、8PSK。

4.2 最優參數值的確立

在實際應用中，需要事先確立向量機中兩個參數(懲罰因子c和核參數σ)，不同的參數值，向量機的分類性能也不盡相同。利用粒子群算法[7]來尋找最優的參數值，參數σ、c的搜索空間均設為0～1000，以分類正確率作為粒子群算法的適應度值。流程如下：

1）初始化種群中粒子的位置（σ、c）和速度。

2）根據不同的核參數σ、c，計算各粒子的適應度值（分類準確率），并得到各粒子迄今為止最優位置和群體迄今為止最優粒子位置。

3）根據式(7)計算自適應慣性權重：

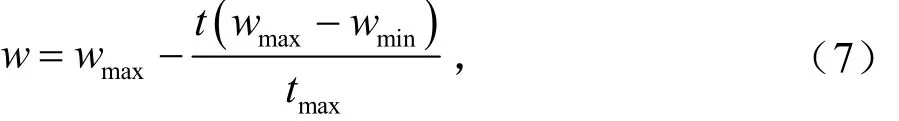
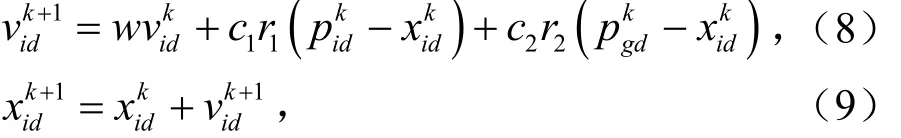
更新粒子速度和位置。

4）判斷是否滿足最大迭代次數。若滿足，算法結束并輸出最優參數值和正確率，否則，迭代次數加1，轉向步驟2。

4.3 性能仿真與分析

每種信號提取樣本數為150 個，其中50 個樣本用于向量機的訓練，100個樣本用于正確率的測試，得到分類正確率曲線如表2所示。

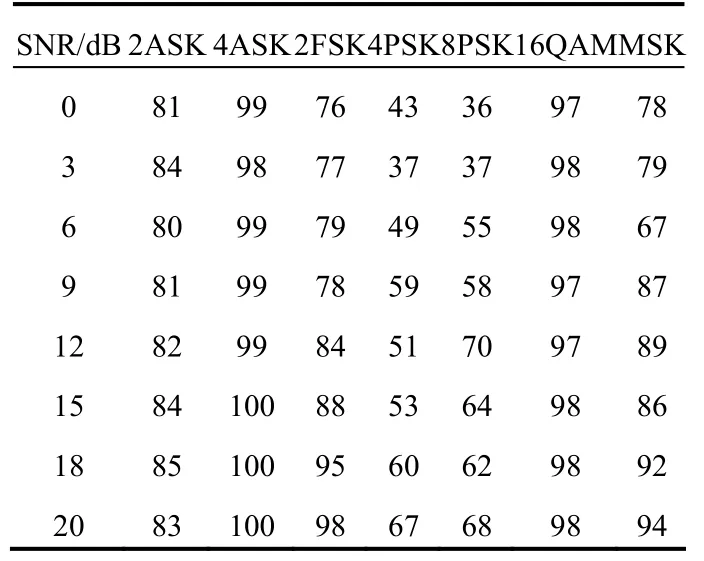
表2 不同調制方式分類正確率(單位∶%)

計算機仿真結果表明：在信噪比為0～20 dB的情況下，基于改進第二代小波的特征識別方法能夠得到較高的調制模式正確識別率，說明新算法能夠很好的分析信號，證明其具有良好的有效性。

文獻[8]中利用 sym4基小波分解細節系數，然后計算標準差作為特征參數。sym4小波具有很多的優良特性，因此選用此小波函數進行對比很有意義。仿真得到兩種小波分類正確率曲線如圖2所示。

仿真結果表明：改進的提升小波與sym4小波相比，能夠得到更高的調制模式識別正確率，說明新算法能夠更好的分析信號，具有更好的有效性。

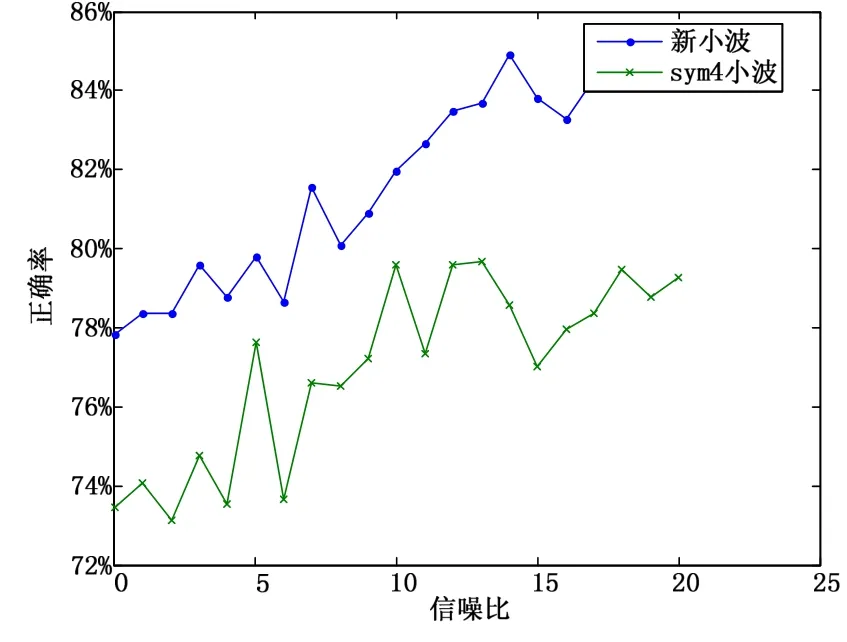
圖2 分類正確率隨信噪比變化示意

5 結語

針對 7種常用數字調制信號進行了計算機仿真，仿真結果表明：改進的提升小波在使特征值具有更好的特征均值和方差的同時，降低了算法的復雜度，提高了識別的正確率，充分說明新算法具有更好的有效性和工程應用性，但是在識別PSK信號時效果欠佳。如何改進PSK信號的識別正確率，是接下來需要研究的方向之一。

[1] 唐峰,蔣興浩,孫錟鋒,等.基于多特征融合的運動對象識別算法[J].信息安全與通信保密,2012(03):57-58.

[2] 楊揚,鄧家先,吳昊.提升小波高速分解的系統設計與實現[J].通信技術,2011,44(04):16-18.

[3] 段晨東,姜洪開,何正嘉.一種改進的第 2代小波變換算法及應用[J].西安交通大學學報, 2004,38(01):47-50.

[4] FERNANDEZ G, PERIASWAMY S, SWELDENS W. Liftpack:a Software Package for Wavelet Transforms Using Lifting[J]. Proc of SPIE on Wavelet Applications in Signal and Image Processing. 1996,2825(04):396-408.

[5] 張學工.關于統計學習理論與支持向量機[J].自動化學報, 2000, 26(01):32-42.

[6] 王玲霞,袁佳,張效義.基于小波包變換的輻射源信號特征提取和識別[J].通信技術,2009,42(03): 215-217.

[7] KENNEDY J, EBERHART R C. Particle Swarm Optimization[C].USA:IEEE, 1995:1942-1948.

[8] 閆朋展.基于特征選擇和BT-SVM的數字調制模式識別研究[D].安徽:解放軍電子工程學院,2011.