基于橢圓曲線的跨域端到端口令認證密鑰協商協議

張曉敏

陜西省行政學院 陜西 710068

0 前言

伴隨著自組織網絡、移動網絡和普適計算等現代通信環境的快速發展，在跨域的環境下構造安全的端到端信道成為必然。跨域認證密鑰協商協議主要是解決此類問題的，為處于不同域中的用戶建立安全信道。口令因其容易記憶，易于選取，節省存儲空間，適合實際應用等特點成為最簡單的認證方法。跨域的端到端的口令認證密鑰協商協議(C2C-PAKA)的主要目的是使分布在不同域中持有不同口令的兩個客戶端可以在各自服務器的協助下實現相互認證并協商出共同的會話密鑰。

2002 年，Byun等人提出了第一個跨域的端到端的認證密鑰協商協議。然而，文獻[2]指出該協議不能抵抗字典攻擊。隨后，對此協議的其它類型的攻擊或效率改進以及協議的變形在文獻[3-6]中被相繼提出。但是，這些協議的變形都僅提供了啟發式的安全分析。在文獻[7]中，Byun等人首次提出了跨域的端到端的口令認證密鑰協商協議的形式化證明方法并給出了一個具有安全性證明的協議。其后，王等人指出如果服務器之間共享的密鑰泄露，文獻[7]中的協議易遭受口令泄露模仿攻擊和中間人攻擊。在文獻[9]中，Phan等人展示了如何對文獻[7]的協議進行在線不可測字典攻擊。此外，文獻[10]指出Byun等人的安全模型中的缺點并在改進后的模型中證明了一個新的跨域的端到端認證的密鑰協商協議的安全性。然而，文獻[10]存在使用計算負載高的公鑰加密、協議的輪數沒有達到最優并且改進的安全模型刻畫的安全性質較少等問題。

以上的方案中用戶從對應服務器獲得認證所需信息，而后直接通信以建立會話密鑰，這種方式稱為直接通信架構。此外，用戶還可以采用間接通信架構，通過相應的服務器來建立會話密鑰，這樣就減少了用戶交互輪數。在文獻[11]中，Ota等人采用了間接通信架構提出可普遍組合的C2C-PAKA方案，但需要的輪數較多。文獻[12-13]提出了采用間接通信架構的跨域認證方案。但是在這兩種方案中，用戶和服務器之間共享的秘密信息僅有口令，因此，方案難以抵御密鑰泄露模仿攻擊和不可測在線字典攻擊等復雜攻擊。吳等人采用公鑰加密技術提出了一種認證方案，可以抵御不可測在線字典攻擊、未知密鑰共享攻擊和密鑰泄露模仿攻擊等，并且輪效率較高。Yoneyama等人引入服務器的公私鑰對抵抗此類攻擊。 但是，這兩個方案采用模冪運算或對運算等復雜運算，通信代價和計算代價都偏高，不易于實現。

本文中，我們基于橢圓曲線上的離散對數問題，在直接通信架構下給出一個跨域的口令認證的密鑰協商協議。該協議中，誠實的服務器是不能獲取任何關于會話密鑰的值。域內服務器通過口令實現和用戶的相互認證，不同域的服務器之間通過公私鑰對實現對對方的認證，而用戶之間借助于各自域中的服務器的協助實現相互認證。與同類協議比較，該協議具有較小的通信負擔和計算負擔，更易于實現。此外，協議還能夠抵抗字典攻擊、口令泄露模仿攻擊和未知會話密鑰共享攻擊等通用攻擊類型，同時能夠實現前向安全、無密鑰控制和已知會話密鑰安全等安全屬性。

1 預備知識

p是有限域Fp的元素個數，其中p是大素數(長度大于160，或p=2m，m為正整數) 。定義Fp上的橢圓曲線E：y2=x3+ax+b ，當p＞3；或y2+xy=x3+ax2+b，當p=2。P是E（Fp）中階為q的一個基點，q為大素數。

1.1 橢圓曲線上離散對數問題(DLP)

G是由點P生成的循環加群，給定Q，找到正整數n，使得Q=nP。

1.2 橢圓曲線Diffie-Hellman 密鑰交換協議(ECDH)

A選擇隨機數a∈Fq并計算PA=aP發送給B；B選擇隨機數b∈Fq并計算PB=bP發送給A。A和B分別計算aPB，bPA從而得到共同的會話密鑰K=（ab）P。

2 協議描述

2.1 公開參數

P是q階循環加群G的生成元， H：｛0,1｝*→｛0,1｝l是哈希函數；A,B是用戶，pwA，pwB是用戶相應的口令；VA和VB分別是用戶A和B分別與對應的服務器SA和SB共享的信息。此外，服務器SA和SB分別持有公私鑰對(PrSA,PKSA)和(PrSB,PKSB)。

2.2 初始化過程

本部分中，我們將給出一個安全高效的C2C-PAKA協議NC2C-PAKA。該協議中有四個參與方，分別為A，SA，B和SB，其中A和B分別處于SA和SB的域中。

初始化階段：客戶端A、B和相應的服務器共享利用算法gpw獲取的口令pw，SA和SB分別存儲A、B的驗證元：VA=H（IDSA,IDA,pwA）P ，VB=H（IDSB,IDB,pwB）P 。此外，初始化階段還定義了一系列的密碼學函數和參數，例如Hash函數等。

算法gpw口令生成算法：從口令字典中隨機選取口令pw給客戶端。

算法?注冊算法：客戶端將其口令pw與其服務器共享，服務器同時將其選取的公開參數發送給客戶端。

協議描述 NC2C-PAKA協議的具體描述見下文，協議運行的一個實例如圖1所示。

(1) A選取隨機值rA∈Zq*，計算TA=rAPKSA+H(IDA,pwA)P 和RA=rAP。隨后，A利用TA加密消息｛IDA,IDB,IDSA,IDSB,RA｝，然后將加密結果和RA一起發送給SA。

(2) 收到消息后，SA先利用RA計算TA′=PrSARA+VA，然后用TA′解密收到的消息，將解密后的消息和接收到的消息進行對比。如果各項數值不一致，則協議終止。如果驗證成功，SA選取sA∈Zq*，計算，然后利用KAB加密消息｛IDA,IDB,IDSA,IDSB,R*A｝ ，并將加密結果發送至SB。

(3) 與此同時，B和SB同樣執行步驟(1)(2)中相應的操作。

(4) SA收到加密消息｛IDB,IDA,IDSB,IDSA,RB*｝后，用KAB解密消息，對比各參與方的身份信息。如果驗證沒有通過，協議中止。否則，SA計算，然后將消息發送給A。

(5) 同時，SB將會收到加密消息｛IDA,IDB,IDSA,IDSB,R*A｝，用KAB解密消息，對比各參與方的身份信息。如果驗證沒有

通過，協議終止。否則，SB計算，然后將消息發送給B。

(6) A收到SA的消息后，利用接收到的計算并驗證α′=?α。如果驗證失敗，則協議終止。否則，A按如下方式計算最終的會話密鑰：

(7) B執行和A在第五步中類似的操作，通過驗證收到的消息β來驗證的合法性。如果驗證通過，則按如下方式計算和A的共同會話密鑰：

正確性：如下所述，誠實執行協議后，各用戶能夠計算獲得相同的會話密鑰。

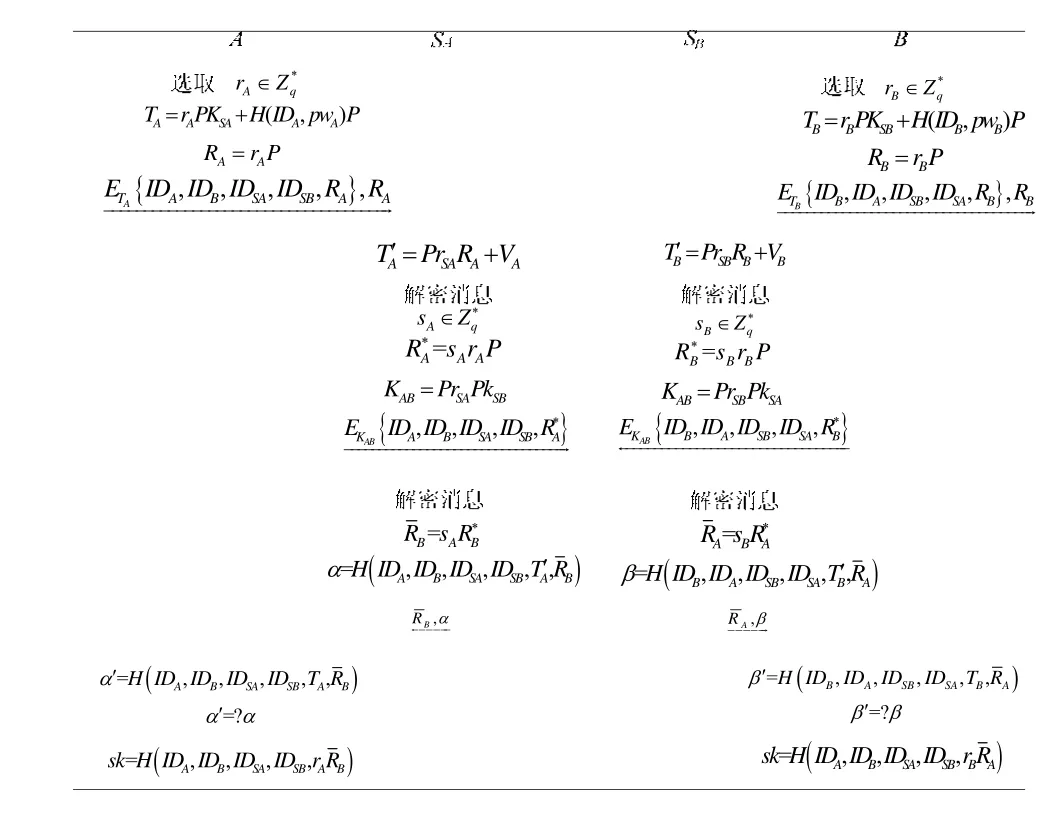
圖1 NC2C-PAKA協議運行實例

3 效率和安全性分析

3.1 效率分析

我們分析協議的通信、計算和輪復雜度以及存儲開銷和實現成本。我們的協議中，用戶A和服務器SA與用戶B和服務器SB各自之間的交互是同步進行的。此外，服務器SA和SB之間的信息傳遞也是并行的。因此，我們減少了通信步驟，降低了通信代價。與同類協議比較，我們的協議避免了消耗較高的模冪運算和對運算。具體比較結果如表1所示。為了比較計算復雜度，我們使用了下列符號表示消耗的時間以及采用如下對比關系： TS表示一次對稱加密所需時間；TPa表示一次對運算所需時間；TMul表示一次點乘運算所需時間；TExp表示一次模冪運算所需時間，并且1TExp?240TMul；TEC Mul表示一次橢圓曲線上的點乘運算所需的時間，1TECMul?29TMul；由于哈希運算所需時間較少，在此我們將其忽略。

表1 效率比較

3.2 安全性分析

(1) 抵抗字典攻擊。首先，在離線字典攻擊中，攻擊者利用其截獲的信息驗證猜測的口令是否正確。該協議中，以用戶A為例，協議中傳遞的信息與口令相關的僅有以TA′作為部分輸入的和以TA加密的消息｛IDA,IDB,IDSA,IDSB,RA｝。攻擊者在各輪中通信中截獲這些信息，由于TA′=PrSARA+VA和TA=rAPKSA+H(IDA,pwA)P，這里，PrSA是服務器SA的私鑰，rA是用戶選取的隨機數，公開信道上傳遞是其橢圓曲線上的離散對數形式RA。因此，敵手沒有足夠的信息來驗證其猜測的口令是否正確。離線字典攻擊可以避免。其次，本協議可以抵抗在線字典攻擊，因為服務器A在解密消息后需要驗證被加密的信息是否和自己掌握的信息一致，以此來確定用戶是否真正知道口令。一旦驗證失敗，服務器就會意識到是誰的口令已經作為在線字典攻擊的目標了。如果失敗的次數超過預定的門限值，服務器A就會通知該用戶停止使用該口令并啟用新的口令。

(2) 抵抗口令泄露模仿攻擊。口令泄露模仿攻擊是指如果一個用戶的口令泄露，敵手可以偽裝成其它用戶來和該用戶進行交互協商會話密鑰，以達到其攻擊目的。本協議中，假設用戶A(B)的口令泄露，敵手可以利用該口令計算口令信息VA=H（IDSA,IDA,pwA）P 或 (VB=H（IDSB,IDB,pwB）P )，但敵手仍然無法獲取服務器SA(SB)的私鑰信息PrSA(PrSB)。因此，敵手仍然不能計算有效的驗證信息α(β)，也就是說，敵手不能成功偽裝為服務器與用戶進行交互。我們的協議能夠抵抗口令泄露模仿攻擊。

(3) 抵抗未知會話密鑰共享攻擊。未知會話密鑰共享攻擊是指敵手致使用戶A認為自己與用戶B共享了一個會話密鑰，實際上這個會話密鑰是用戶A和敵手共享的。產生此類攻擊的根本原因是協議執行時用戶身份信息被替換，同時其它參與方沒有發現。我們的協議中， 協議所有參與方的身份信息均和協議運行的其它信息一起經過只有通信雙方才能產生的密鑰加密傳遞的，接收方可以驗證發送方的消息是否被篡改。因此，我們的協議從根本上避免了此類問題的發生，協議能夠抵抗未知會話密鑰共享攻擊。

(4) 前向安全性。由于最終的會話密鑰是由隨機數構成的，而隨機數是由各參與方隨機選取的，在協議交互過程中，傳遞的信息是隨機數所對應的離散對數形式。由于離散對數問題的困難性，攻擊者即使獲得用戶與服務器的長期密鑰，仍然無法獲得隨機數，因此不能計算出會話密鑰。所以協議提供前向安全性。

(5) 無密鑰控制。協議使用Diffie-Hellman密鑰交換協議的思想協商會話密鑰，此外rA是由用戶A隨機選取的，sA是由服務器SA隨機選取的，rB是由用戶B隨機選取的，sB是由服務器SB隨機選取的。因此，任何一方不能單獨控制會話密鑰的選擇，達到了協議無密鑰控制的目的。

(6) 已知會話密鑰安全。攻擊者攻破一次通信的會話密鑰，無助于攻破另一次通信的會話密鑰。這是因為通信雙方最終得到的會話密鑰是由隨機數構成，由于兩次通信使用的是不同的隨機數，這種隨機數的不相關性使得攻擊者即使攻破了一個會話密鑰也無法利用該信息攻破另一次通信的會話密鑰，以此實現已知密鑰安全。

[1] Byun J.,Jeong I.,Lee D.,et al.Springer Berlin/Heidelberg.2002.

[2] Chen L. A weakness of the password-authenticated key agreement between clients with different passwords scheme.ISO/IEC JTC 1/SC27 N3716.

[3] Kim J.,Kim S.,Kwak J. et al.Springer Berlin/Heidelberg.2004.

[4] Byun J.W.,Jeong I.R., Lee D.H.,et al.assword-Authenticated Key Exchange between Clients with Different Passwords.In Proceedings of Proceedings of the 4th International Conference on Information and Communications Security.2002.

[5] Phan R.,Goi B.M.Springer Berlin/Heidelberg.2005.

[6] Wang S.,Wang J.,Xu M.Springer Berlin/Heide lberg. 2004.

[7] Byun J.W.,Lee D.H.,Lim J.I.EC2C-PAKA：An efficient client-to-client password-authenticated key agreement[J].Information Science.2007.

[8] J. Wang, Y.Z.Cryptanalysis of a client-to-client password--authenticated key agreement protocol.2008.

[9] Phan R., Goi B.M.Springer Berlin/Heidelberg.2006.

[10] Feng D.G.,Xu J.Springer Berlin/Heidelberg.2009.

[11] Ota,.,Yoneyama,K.,Kiyomoto,S.,Tanak,T.,Ohta,K.Universal ly Compos-able Client-to-Client General Authenticated Key Exchange[J]. IPSJ Journal.2007.

[12] Yin,Y.,Bao, L.Secure Cross-Realm C2C-PAKE Protocol.In：Batten,L.M.,Safavi-Naini,R.(eds.) ACISP 2006.LNCS,4058,Springer,Heidelberg (2006).

[13] Wang,F.,Zhang,Y.A New Security Model for Cross-Realm C2C-PAKE Protocol.In： Cryptology ePrint Archive：2007/342(2007).

[14] Wu, S.,Zhu, Y.Password-Authenticated Key Exchange between Clients in a Cross-Realm Setting.In： Cao,J.,Li,M.,Wu,M.-Y.,Chen, J.(eds.) NPC 2008. LNCS,vol.5245, pp. 94-104.Springer, Heidelberg (2008).

[15] Kazuki Yoneyama, Haruki Ota, Kazuo Ohta. Secure cross-realm client-to-client password-based authenticated key exchange against undetectable on-line dictionary attacks.Proceedings of the 17th international conference on Applied algebra, algebraic algorithms and error-correcting codes,Bangalore, India, 257-266, Springer-Verlag(2007).