軌道不平順數字特征分析
梁志明,劉秀波,李紅艷,李海浪
(中國鐵道科學研究院 基礎設施檢測研究所,北京 100081)
軌道不平順是指軌道幾何位置相對軌道設計位置的變化。由于目前的測量方法無法得到軌道幾何絕對位置,軌道不平順一般由左右高低、左右軌向、水平、三角坑和軌距來描述和控制。軌道不平順的形成和發展是很多帶有隨機性的因素共同作用的結果。這些因素包括鋼軌的初始不平順、線路鋪設誤差、道床路基的不均勻殘余變形、線路維修和大修誤差等。所有這些因素都使得軌道不平順具有隨機性。隨機性的軌道不平順包含許多不同幅值和波長的諧波成分,波長范圍很寬,波長為0.01~200.00 m的軌道不平順都很常見。根據國內外有關資料和專家的意見[1-5]波長1 m以下的軌面短波不平順主要由鋼軌接頭、焊縫、不均勻磨耗、鋼軌擦傷、剝離掉塊、波浪和波紋磨耗以及軌枕間距等因素形成;波長為1~4 m的軌道不平順主要由鋼軌在軋制過程中形成的周期波和鋼軌在使用中形成的波浪磨耗引起;波長為4~30 m軌道不平順主要由道床路基的殘余變形不均勻沉降、道床彈性密實度不均勻、各部件間隙不等、接頭或焊縫形成的以鋼軌長為基長的復雜周期波,中、小橋墩、橋臺、橋頭區、涵洞、道口等軌道剛度變化和橋梁動撓度等原因形成的不平順;波長為30~200 m軌道不平順多由道床路基沉降不均、路基施工過程中形成的先天性不平順和跨度較大的橋梁靜動撓度等原因形成的不平順;200 m以上的軌道不平順是由地形起伏、線路坡度變化等原因形成的。軌道不平順的隨機性決定了軌道不平順不能用一個明確的數學表達式來表示,只能用描述隨機數據的“均方值”、“標準差”、“功率譜密度”等統計函數來表示軌道不平順的隨機性特征。
以往軌道不平順譜的計算都假設軌道不平順具備平穩性和正態性,因此常取一段或幾段線路的軌道不平順譜表示整體軌道不平順譜。但在軌道不平順檢測過程中發現,軌道不平順常常具有非平穩特征。如果軌道不平順隨機數據樣本是非平穩的,那么目前軌道不平順譜的計算和統計方法就不合理。因此,對實際軌道不平順的平穩性和正態性進行研究很有必要。
1 軌道不平順平穩性和正態性檢驗方法
1.1 平穩性檢驗方法
最常用的方法有輪次檢驗[6]和逆序檢驗[7],均為非參數檢驗。
1)輪次檢驗
輪次檢驗原理是將被分析的隨機信號分成若干段,并求出各段的均方值(或者均方根值、方差、標準差等),組成一個新時間序列。如果信號是平穩的,則新序列的變化將是隨機的,而且沒有趨勢項。檢驗步驟是先求出這些均方值的中值,再逐個地將各段的均方值與中值比較,其中大于中值的均方值記為“+”,小于中值的均方值記為“-”,這種從“+”到“-”和從“-”到“+”變化的次數稱為輪次數,用 r表示。一個序列的輪次數表明了同一隨機變量的測量值是否獨立。平穩隨機過程的輪次數將滿足一定的統計規律,具有如下的均值和方差
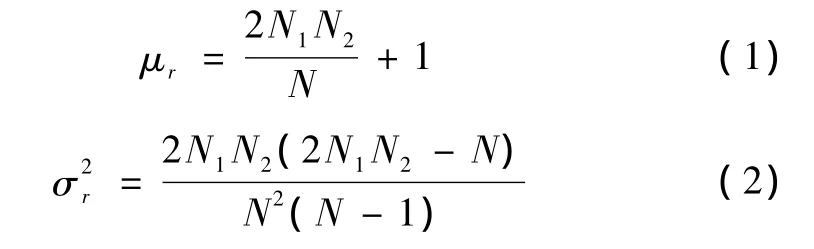
式中 N——樣本記錄等分段數;
N1——均值大于中值段的個數;
N2——均值小于中值段的個數;
r——輪次數。
對于平穩隨機過程,當N→∞時,有 N1=N2,此時均值和方差簡化為
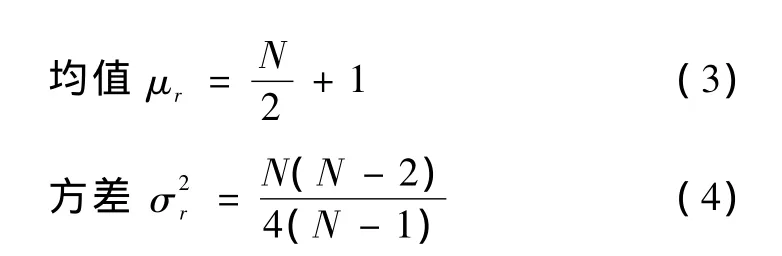
因此,式(1)是式(3)的一種逼近關系,其逼近程度與N的大小有關,在給定置信度和N的情況下,可以確定置信區間即

如果求得的輪次數r落在置信區間內,則所測量的隨機過程是平穩的。落在置信區間外則是非平穩的。式(5)中的上、下限值可以由輪次查表得。
2)逆序檢驗
逆序檢驗是一種對均值或方差可能存在某種趨勢進行檢驗的方法。首先由時間序列求出一個大致不相關的均值或方差的序列(把整個數據記錄分成M段,然后求各段按時間平均的均值和方差)。設該序列為y1,y2,…,yM,每當出現 yj> yi(j> i,i=1,2,…,M -1)時,定義為yi的一個逆序。對于下標為i的已知值yi,其逆序數定義為與 yi相應的逆序的個數 Ai。逆序總數為

可以證明,以隨機數序列出現的A的平均值和方差為

則統計量

式中,A為逆序總數,A1為 A的平均值,A2為 A的方差。
漸近服從正態分布N(0,1)。根據M算出E[A],然后按實際逆序數A得出μ值。如果μ值是處在±2之內,則可接受“序列無趨勢”假設;否則拒絕該假設(在0.05顯著水平上)。顯然,如果 A很大,表明序列均值(或方差)有上升的趨勢,而 A很小,表明序列的均值(或方差)有下降的趨勢。
逆序非平穩趨勢檢驗方法具有局限性,但對于單調的趨勢隨機數據序列是有效的。
1.2 正態性檢驗
在概率論與數理統計中,常用偏度和峰度值檢驗隨機信號的正態性。滿足正態分布隨機信號的偏度和峰度近似服從正態分布。任意隨機信號樣本函數的偏度為S,峰度為K。可以根據下面的統計量對隨機信號進行正態性檢驗[8]。
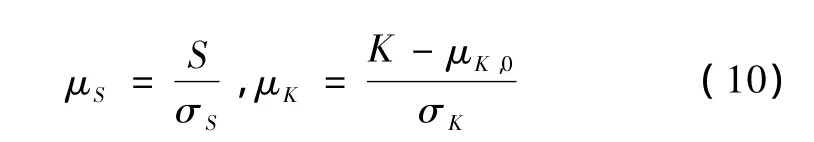
式中
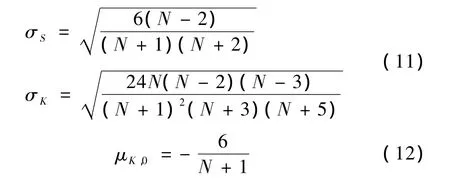
式中,N為樣本個數。
定義概率函數為
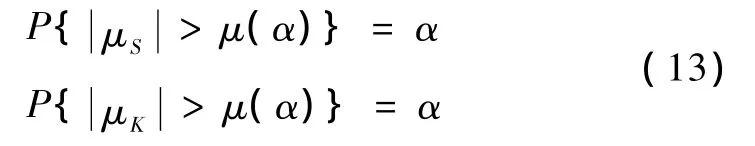
其中,α為顯著水平,μ(α)可由查表得到。
根據式(10)計算隨機信號樣本函數的 μS和 μK,由表1,查 μ(α)則有:且,隨機信號為正態分布;或,隨機信號為非正態分布。

表 1 μ(α)
2 軌道不平順統計量計算分析
2.1 軌道不平順的平穩性
圖1至圖3分別為軌向、高低、軌距和水平的均方根變化曲線。從圖中可以看出:如果把線路劃分成不同區段,均方值變化趨勢可以滿足平穩性條件。這說明不同的線路條件、施工方式、維修方式、運營條件和地理環境等因素影響了軌道不平順產生、發展和變化。線路較長時,由于線路常常劃分成不同工程局施工、不同鐵路局和工務段維修,使得線路設備和維修方式不盡相同,而且受不同區域地質和氣候等因素影響,使得較長線路不滿足平穩性條件。因此,在計算軌道不平順譜時,不能通過局部區段軌道不平順譜代替整條線軌道不平順譜,而且也不能用簡單平均方式計算軌道不平順譜。
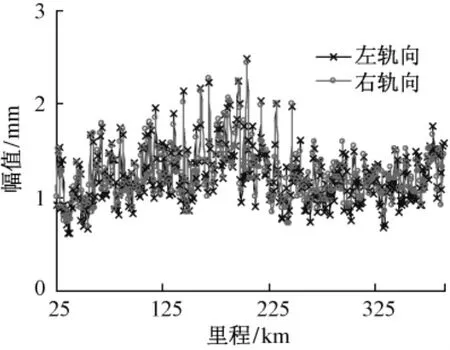
圖1 軌向均方根變化曲線

圖2 高低均方根變化曲線

圖3 軌距和水平均方根變化曲線
2.2 軌道不平順正態性
從圖4軌道不平順偏度變化曲線可以看出:水平不平順偏度偏離零線較大,而且隨里程變化較大,水平偏度大值主要出現在曲線頭尾,而軌距偏度大值主要出現在道岔附近。
從圖5軌道不平順峰度變化曲線可以看出:軌距不平順峰度除局部地段遠大于3外,其余都接近3;水平不平順峰度大于3。
由以上分析可知,部分里程不滿足正態性。進一步研究發現,峰度大的位置一般包含幅值較大的長波局部不平順,如圖6所示線路設置的超高對水平不平順的影響,正是這一原因使得軌道不平順不能滿足正態性,同時也表明軌道不平順含有非平穩特征成分或趨勢項。
3 結論
研究了軌道不平順數字特征的統計量和檢驗軌道不平順平穩性和正態性的方法。利用實測的軌道不平順數據對軌道不平順的數字特征、平穩性和正態性進行了研究。通過研究得到以下結論:
1)按1 000 m長度計算,軌道不平順數據絕大多數里程不滿足正態性條件。長波大幅值局部不平順是產生軌道不平順不滿足正態性的主要原因。
2)線路局部區段滿足平穩性條件,但整條線路基本不滿足平穩性條件。
[1] 趙國堂.高速鐵路無碴軌道結構[M].北京:中國鐵道出版社,2006.
[2] 袁長卿,高月婷.軌道不平順性對高速鐵路的影響[J].鐵道建筑,2007(增):109-112.
[3] 陳憲麥,楊鳳春,吳旺青,等.秦沈客運專線軌道譜的研究[J].鐵道建筑,2006(8):94-97.
[4] COENRAAD ESVELD.ModernRailwayTrack(Second Edition)[M].Holand:MRT-Productions,2001.
[5] 楊飛,黎國清,劉金朝,等.高速鐵路軌道不平順預設試驗最大幅值的研究[J].鐵道建筑,2011(7):112-115.
[6] 劉秀波,吳衛新.鋼軌焊接接頭短波不平順功率譜分析[J].中國鐵道科學,2000,21(2):26-33.
[7] 楊位欽,顧嵐.時間序列分析與動態數據建模[M].北京:北京理工大學出版社,1988.
[8] 中國電子、儀器儀表學會信號處理學會《振動數字信號處理程序庫》編委會.振動數字信號處理程序庫[M].北京:科學出版社,1988.

