Fault Diagnosis of Bearing Based on Integration of Nonlinear Geometric Invariables

GUAN Zhen-zhen(關(guān)貞珍)，ZHENG Hai-qi(鄭海起)

(Ordnance Engineering College，Shijiazhuang 050003，Hebei，China)

Introduction

Fault characteristic extraction is a most important step in the fault diagnosis of bearing.At the present，the main methods are time-domain amplitude analysis and frequency-domain fault characteristic spectrum analysis.However，these methods sometimes can not get the enough accuracy and stability due to the effect of work environment and nonlinearity characteristics of bearing system.The characteristic parameters which can response the nature of the nonlinear systems are attempted to find for the diagnosis of bearing fault in this paper.Currently，some dynamic characteristic parameters of nonlinear systems(such as fractal dimension，Lyapunov exponent)have been gradually introduced into fault diagnosis，but these methods are mainly based on single parameter which must affect the diagnosis accuracy because it only reflects the nonlinear system from one side.So this paper attempts to integrate the multiple non-linear geometric parameters to improve the diagnosis accuracy of bearing fault.

1 Characteristic Extraction of Nonlinear Geometric Invariable

1.1 Feature Parameter of Fractal Dimension

For complex mechanical system，the fractal dimension［1－2］can reflect the independent variable number of the system status and the complexity degree of its attractor.Here the fractal dimension is introduced into the bearing fault diagnosis to get the nonlinear vibration characteristics.Currently，the parameters which express the fractal dimension are box dimension，information dimension，self-similarity dimension，correlation dimension，each of them has their own characteristics.As the correlation dimension can be estimated from time series signals，its calculation is simple，and it can reflect the inherent relation of engineering signal.So the correlation dimension is chosen as fault characteristic parameter in this paper.Its calculation method is shown as{xk:k=1，…，N}is a test time series，we extend them tomdimension space and get a new time series with phase space reconstructable technology

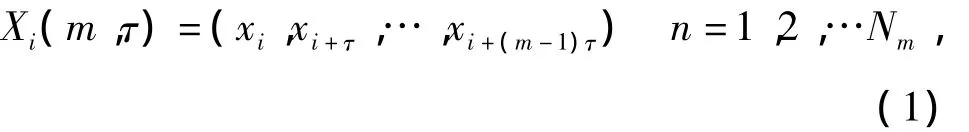
whereτis delaying time，τ=kΔt，Δtis sampling interval，kis integer.

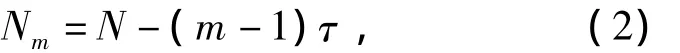
whereNis the number of time series，mis embedding dimension.We choose one pointXjfromNmand calculaterijbetween the test point andXj

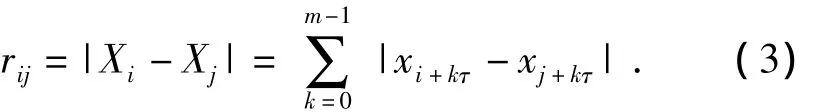
The correlation integral functionC(r)is defined as

whereHis Heaviside function

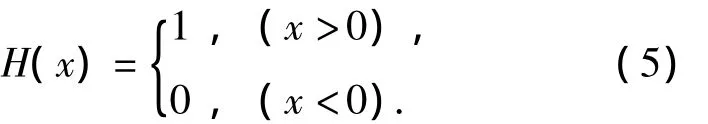
Whenris enough small，the following formulations are got

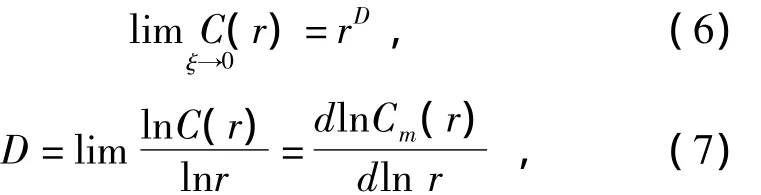
whereDis fractal dimension.

1.2 Lyapunov Exponent Feature Parameter

Lyapunov exponent［3－4］describes quantitatively the average rate of phase space orbit contraction or divergency.Its minimum value determines the speed of orbit contraction while its maximum value decides the speed of orbit divergency，namely，the maximum Lyapunov exponent can reflects the changing degree of attractor resulting from the initial conditions.So it can be used to reflect the attractor“strange”level of nonlinear system.

The methods of calculating Lyapunov exponent from the time sequence are main Jocobian method，Wolf method，and small amount data method.Jocobian method is simple，but can only be used for continuous system described by differential equations;Wolf method has been widely used in the time series prediction research，but it requires the sampling time series to be noise-free or of very low noise;small amount data method does not calculate all of Lyapunov exponent spectrum except for the largest Lyapunov exponent，and its result is affected significantly by embedding dimension.We choose Wolf method to calculate the largest Lyapunov exponent based on its extensive application and the bearing vibration signals which are filtered.Its calculating method is as follows.

Step 1 Chose a phase pointXt0in the reconstructed phase space，andX't0isXt0nearest phase point，we calculate the distance ofXt0andX't0

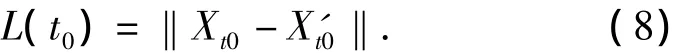
Step 2Xt0andX't0are the start points，and calculate the distances of them when the angle of their distance vector is the smallest after one calculating period.

Step 3 Search the phase pointXt1at the timet1=t0+τ，and calculateL(t1)andL'(t1)according to Step 1 and Step 2.

Step 4 Repeat the above steps until the evolvement getting end pointXk(m，τ)，if the evolvement step isM，the mean of exponent increasing rate is the max Lyapunov exponent

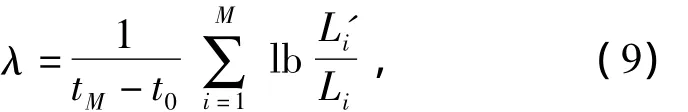
wheretM－t0is the striding row when phase space is reconstructed，Mis iterative time.

1.3 Kolmogorov Entropy Feature Parameter

Kolmogorov entropy［5］is an important parameter of describing chaotic motion and is defined based on entropy.Strange attractor divides the phase space intonunits which scaleεd，and these units are labeled as，…，.If the previously status of this system，，…，is known，thenKn+1－Knshows the needed additional information of the predict system which is in the unit of，which meansKn+1－Knmeasuring the value of lost information from the time(n－1)τtonτ，Kolmogorov entropy is an average value of lost information.

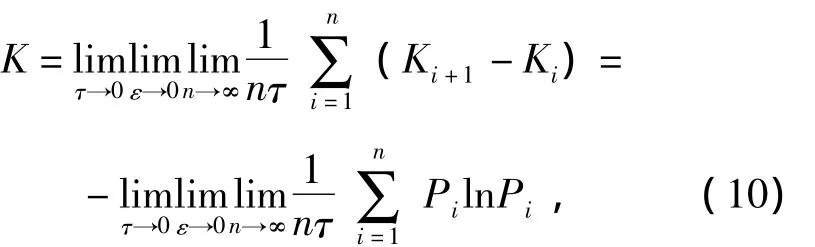
wherePiis the probability ofx(τi)which falls inunit at timeτ，K=0 shows that the system is in cycle movement，K= ∞ shows that the system is in random movement，K＞ 0 shows that the system is in chaotic movement.

The bigger theKvalue is，the more the lost information is，and the greater the chaos degree of system is.SinceKis the lower bound ofqorder Renyi entropy，andKq≤Kq+1，K1=K，soK2entropy seems to be the approximateKentropy.

1.4 Correlation Distance Entropy Feature Parameter

Correlation distance entropy reflects the density of orbit point in the reconstructed phase space，It is calculated as follows

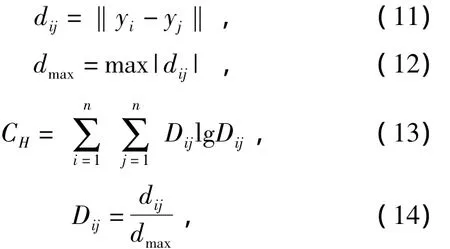
wheredijreflects the distance between the points of phase space，and it also reflects the relative distance between the points after normalizing.CHreflects the parse level of the phase points，and it is an absolute size which is relevant to the number of phase points，so it can not be used generally.Here the parameter of correlation distance entropy is used，which is defined asHd=CH /CHmaxto show the character of bearing system，in which

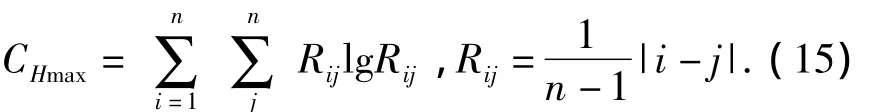
2 Integration of Nonlinear Geometric Invariables Based on Grey Correlation

The nonlinear geometric invariable values can reflect the state of bearing system，but their calculating progresses need to be perfected，and one parameter only reflects one side of the system rather than all the sides.If the fault diagnosis of bearing is based on one of these parameters，the result accuracy will be lower.Therefore，in order to improve the accuracy，this paper presents the integration of nonlinear geometric invariables based on grey correlation.

2.1 Experimental Equipment

We build a gear test-bed in order to validate the validity of the proposed method in this paper，the experimental equipment is shown in Fig.1.The following test data in this paper were acquired from this test-bed.B＆K4508 vibration acceleration sensors are installed on the bearing seats.The vibration signals are acquired on the input bearing which model is 6 206，and the baring crack failure with width of 0.5 mm and a depth of 1mm is implanted in normal bearings by wire cutting method.The sampling bandwidth is 614 kHz，the sampling frequency is 12.8 kHz，and the shaft frequency is 18.5 Hz.

Fig.1 Experimental equipment

2.2 Grey Correlation Theory

Grey correlation theory［6］seems the standard vector as a line in one dimension space.It is used to calculate the geometric similarity between the vector needing to be diagnosed and the standard vector to determine the degree of correlation.

X0is the standard mode

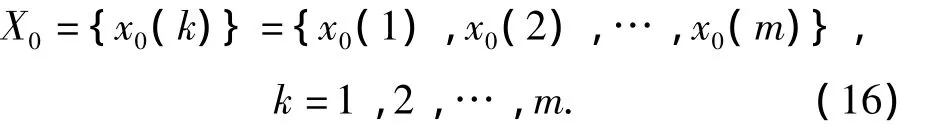
Xiis the mode to be diagnosed

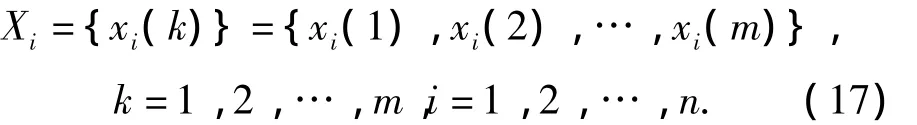
In order to make these data to be in a same magnitude grade，we normalize them

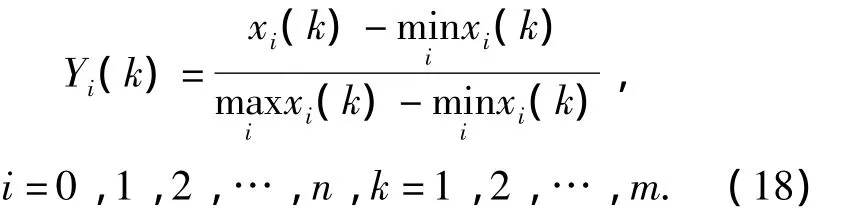
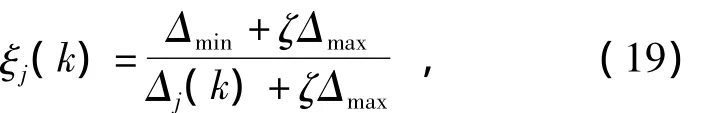
where

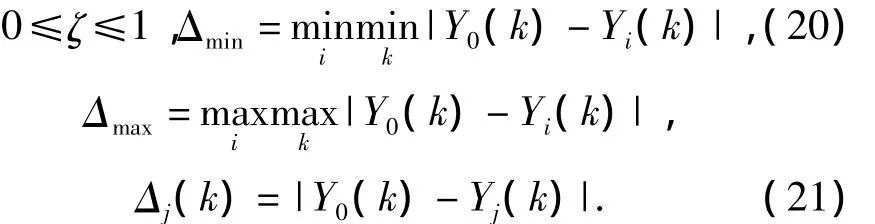
Thus，the grey correlation model is defined as

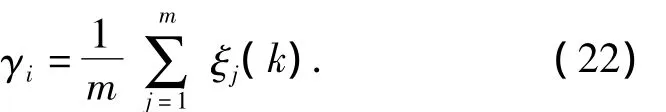
2.3 Fusion Algorithm of Multi-variable

Step 1 Acquire 20 groups of data during experiment(four groups of data with normal bearing;four groups of data with out ring fault;four groups of data with inner ring fault;four groups of data with rolling element fault;four inner ring and outer ring complex faults.).Then EMD and morphological difference methods are used to calculate the nonlinear geometric invariable after filtering noise，respectively.The calculated result is shown in Tab.1.

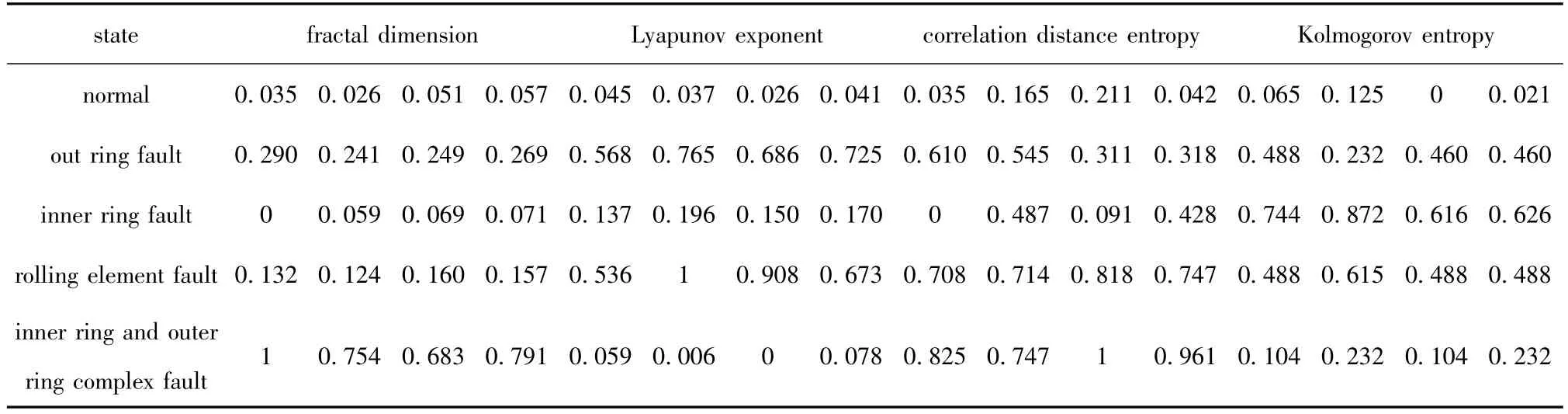
Tab.1 Nonlinear geometric invariables of measured signals(after normalizing)

Step 2 Construct a standard feature set of nonlinear geometric invariables.Since no priori knowledge was used to construct the standard fault feature vector，we used 50 groups of experiment data with 10 groups of each bearing states.The nonlinear geometric invariables were calculated from these states，and the average of 10 groups of data was used as a standard feature vector，which is shown in Tab.2.

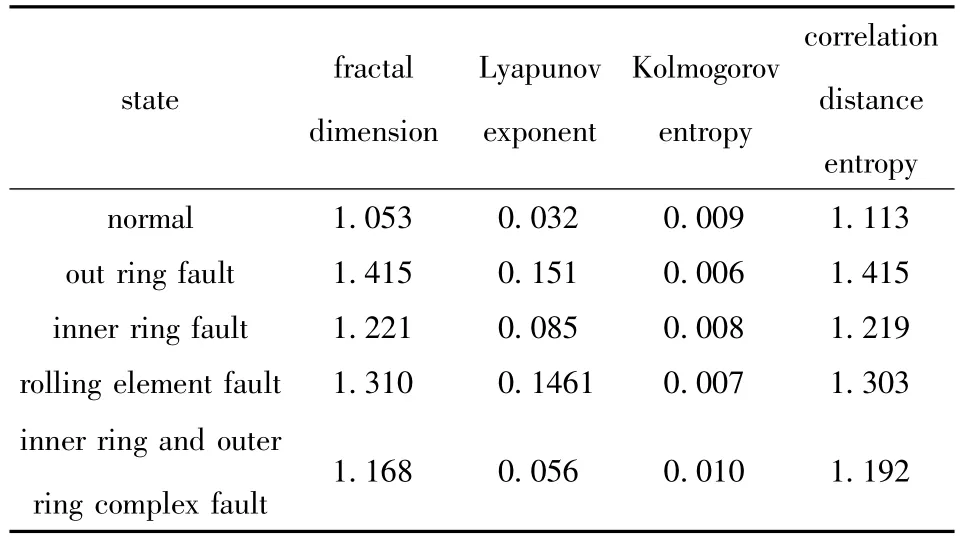
Tab.2 Feature set of standard nonlinear geometric invariables

Step 3 Calculate the correlation.According to Eq.(18)－ (22)and Tab.2，we calculatedriwhich is listed in Tab.3.

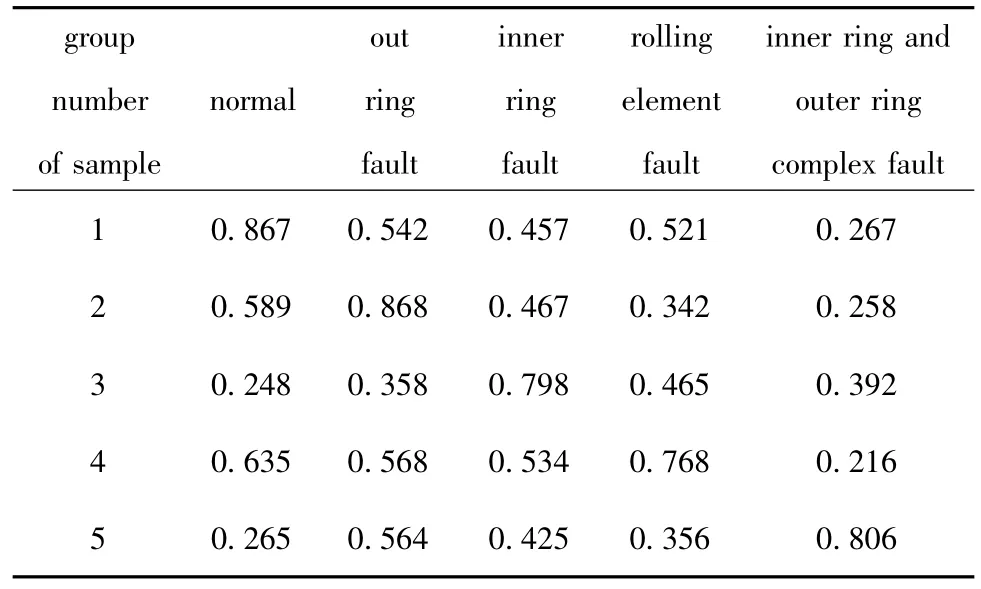
Tab.3 Correlation values

The correlation value reflects the similarity between the standard sample set and the test sample set，the greater the value is，the greater the similarity is.According to this theory，some researchers consider that the max value of correlation corresponds to the fault mode.But this paper thinks that the similarity will be less if the time series have more noise，so we constructed a multi-classification support vector machine to identify the bearing faults.

3 Experiment of Diagnosis

3.1 Fault Diagnosis Based on One Nonlinear Geometric Invariable

The correlation dimension is selected as a feature parameter to diagnose the state of bearing.500 groups of experiment data will be obtained.Each state has 100 groups of data in which 50 groups of data are used as training samples，and the other 50 groups of data are as test sampling data.The average of correlation dimension is the standard value.The result of diagnosis is shown in Tab.4.

3.2 Fault Diagnosis Based on Multiple Nonlinear Geometric Invariables

The correlation dimension，Lyapunov exponent，Kolmogorov entropy，Correlation distance entropy are selected as fault feature set，and the average of the training set，including 50 groups of samples，is the standard value.The correlation between the time series to be diagnosed and the standard value is calculated，these correlations are input into the multi-classification support vector machine.The result of diagnosis is shown in Tab.5.

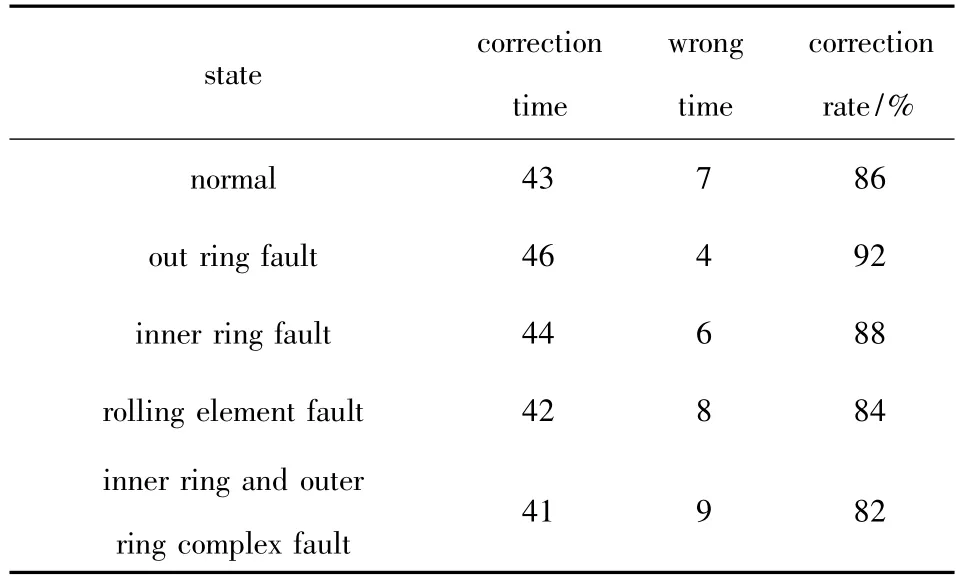
Tab.4 Result of fault diagnosis based on correlation dimension

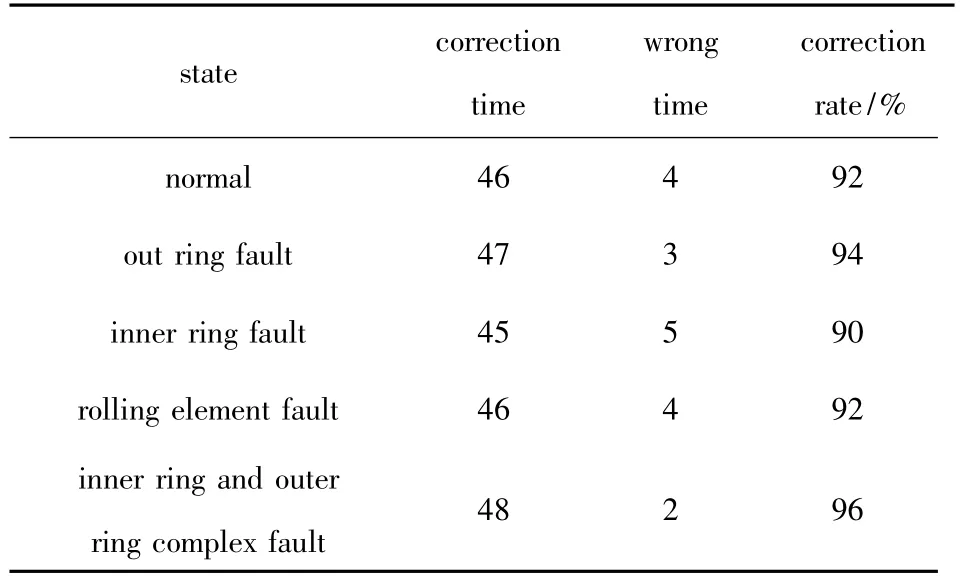
Tab.5 Result of fault diagnosis

By comparing the results of Tab.4 and 5，it can be seen that the precision of fault diagnosis based on multi-nonlinear geometric invariable is better than the result based on one nonlinear geometric invariable.

4 Conclusions

A method of fault diagnosis of bearing based on multiple nonlinear geometric invariables is proposed to resolve the problem that the diagnosis precision is lower when only one nonlinear geometric invariable acts the feature vector.The experiments of bearing fault were carried on.The feature parameters were calculated and integrated based on grey correlation.Experiments show that the method proposed in this paper can improve the precision of bearing fault diagnosis.

［1］TENG Li-na，LIU Tian-xiong，TONG De-chun.Application of correlation dimension to machinery condition monitoring［J］.Journal of Vibration Engineering，2002，15(4):399 －403.(in Chinese)

［2］Grassnerger P.On the fractal dimension of the genon attractor［J］.Physics Letters，1983，7:224 － 226.

［3］Kantz H，Schreiber T.Nonlinear time series analysis［M］.Cambridge:Cambridge University Press，1997.

［4］WANG Li-ying，YANG Shao-pu，WANG Huan.Application of Lyapunov exponents to fault diagnosis of rolling bearing［J］.Noise and Vibration Control，2007，(5):104－106.(in Chinese)

［5］BAI Lei，LIANG Ping.Kolmogorov entropy diagnosis for vibration faults of turbine rotor based on wavelet packet filtering［J］.Journal of Vibration and Shock，2008 ，27(5):148 －151.(in Chinese)

［6］PENG Zheng-hong，SONG Bin.Application of data mining technique based on grey relational analysis in oil-immersed power apparatus fault diagnosis［J］.International Conference on Power System Technology， Powercon，2006，1(6):329 －332.