基于偏差耦合的反演自適應滑模同步控制

彭曉燕 ，范志龍

(湖南大學，湖南長沙410082)

0引 言

分布造紙機、起重機、印染機械等控制系統中同步技術廣泛存在。而電動機作為同步控制系統中的主要驅動設備，在實際應用中，各電動機的同步性能會因外部擾動、各傳動軸的驅動特性不匹配及電動機在運行過程中的繞組溫升等因素的影響而變差，從而降低了系統的精確度和穩定性。因此，系統同步的核心是同步控制，同步控制策略的優劣能直接影響系統的可靠性和控制精確度［1］。

傳統的同步控制多采用精確度不高的主從控制策略，它在穩態時同步性能較好，但在起動停止和外部干擾時會造成很大的同步誤差［2］。為了滿足現代工業的要求，Koren［3］提出交叉耦合控制策略，但是當同步電機數目大于2時，由于交叉耦合控制的速度補償信號難以確定而不適用［4］。2002年Shih等人提出了相鄰交叉耦合控制策略，即每臺電機的控制僅考慮相鄰兩電機的狀態，但當某臺電機受到負載擾動的情況下，它只能通過相鄰電機逐個傳遞給其它電機，這將導致控制延時，從而造成同步誤差。而 Perez—Pinal．F［5］等提出了適用于電機數目多于2的偏差耦合控制，它是通過改進交叉耦合控制而得來的，其改進之處在于每臺電機速度補償信號是通過各個電機狀態反饋得到的。這種控制策略能夠克服其它控制策略的缺點，具有很好的同步性能。

一般控制算法是依靠其系統的精確模型得到的，而永磁同步電動機在運行過程中的精確模型很難得到，因此魯棒性無法達到控制系統的要求。而滑模變結構對系統參數不確定性以及負載擾動等影響因數具有較強的魯棒性，許多學者把其運用到控制系統中，取得了很好的效果［6-7］。本文應用自適應估計不確定上界的擾動，結合反演設計，設計了一種基于反演的自適應滑模控制器，將滑模控制和反演設計方法相結合，即可以簡化反演設計方法的設計，又增加了系統對不確定性的魯棒性，削弱了滑模控制帶來的抖振。同時對五臺電機同步控制系統進行了仿真實驗，仿真結果證明了本文算法的有效性。

1偏差耦合控制策略

偏差耦合控制的速度補償信號是由一臺電動機的速度反饋與其它的電動機速度反饋的偏差乘以相應的增益后再相加得到。乘以增益是用來補償各個電動機之間的轉動慣量的不同，各個速度補償器的反饋放大增益，可以通過其對應電機的轉動慣量求得［8］。其結構示意圖如圖1所示。由圖1可以看出，偏差耦合控制中最重要的部分就是速度反饋模塊，它給每臺電機提供速度補償信號。速度補償器結構如圖2所示，它的作用如同“虛擬地”一樣，將每臺電機在過渡周期和轉矩擾動時的相對速度歸零。圖中:K11、K12為速度反饋耦合增益。

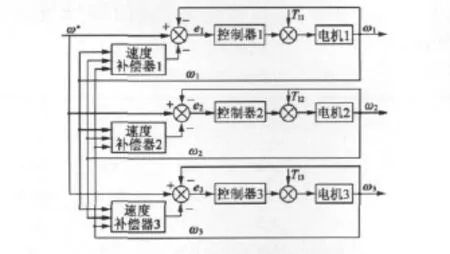
圖1 三臺電機偏差耦合控制系統結構圖

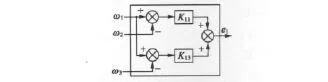
圖2 速度補償器結構圖

2基于反演設計的自適應滑模控制器設計

反演設計的基本思想是將復雜的非線性系統分解成不超過系統階次的子系統，然后為每個子系統分別設計李亞普諾夫函數和中間虛擬控制量，一直“退到”整個系統，直到完成控制律的設計［9］。本文把滑模控制和反演設計相結合設計了控制器，為了避免不確定性的上界，采用自適應算法對其進行了估計。

以五臺電機為例，為實現其同步控制，設計基于反演的自適應滑模控制器。

永磁同步電動機采用id=0的矢量控制方法。將永磁同步電動機的動態方程改寫:

由上述的偏差耦合控制策略可得五臺電機校正后的跟蹤誤差:

則控制器設計步驟如下:

步驟一:五臺永磁同步電動機的動態方程:

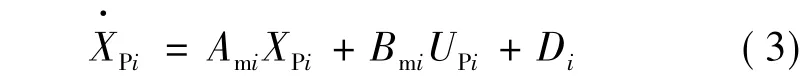
令

對式(4)求導得

取虛擬控制量αi=cizi1，ci為正的常數。

定義李亞普諾夫函數:

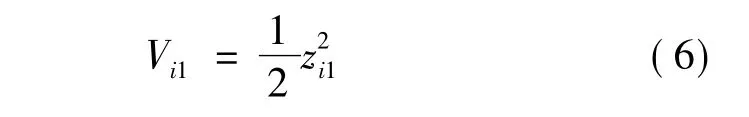
定義:

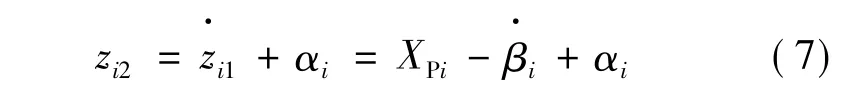
對式(6)求導可得:

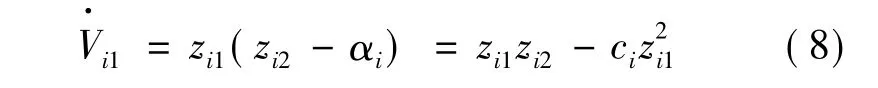
步驟二:對式(7)求導可得:

定義李亞普諾夫函數:

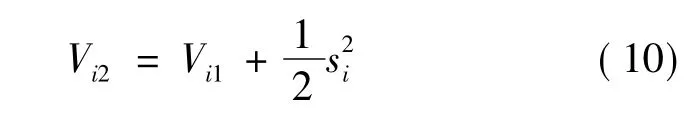
式中:si為切換函數。

定義滑模控制切換函數:

式中:ki＞0。

對式(10)求導可得:

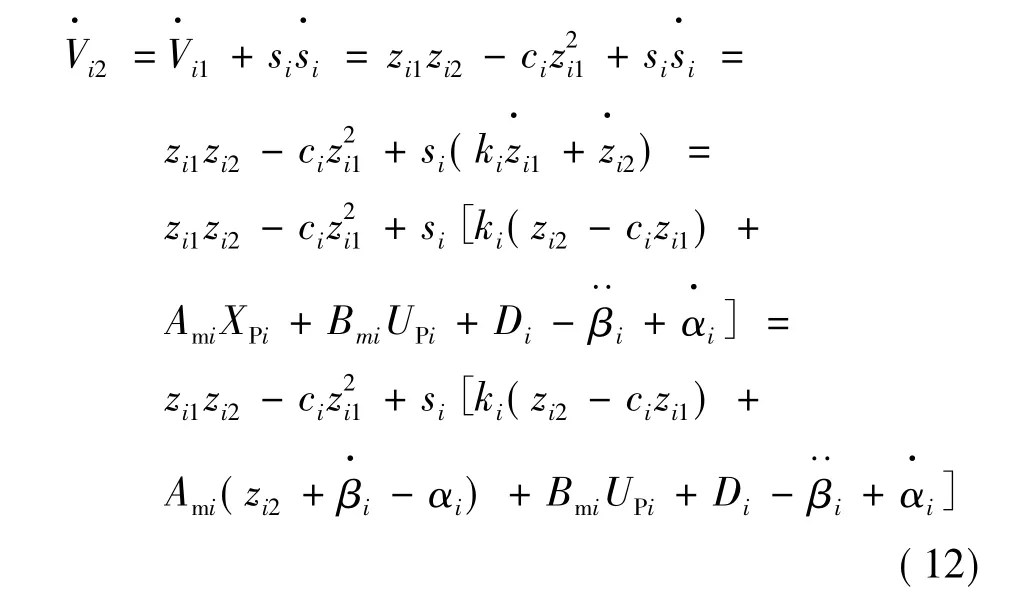
步驟三:設計自適應反演滑模控制器:

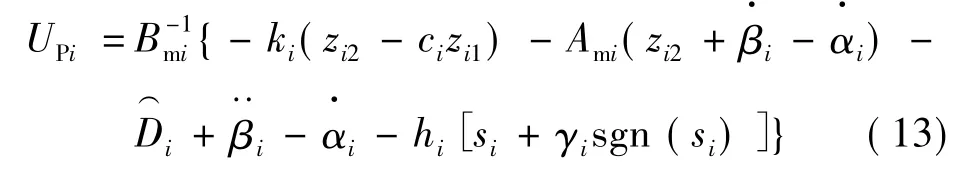
式中:hi和γi為正常數，為不確定參數的上界估計值。

定義李亞普諾夫函數:

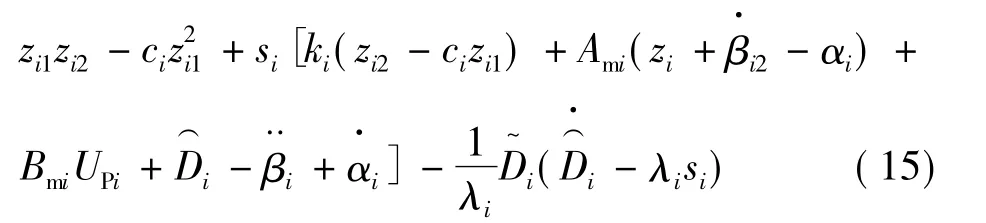
設計自適應律:

將式(13)和式(16)代入式(15)，得:

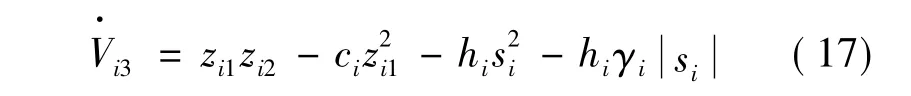
取

則:

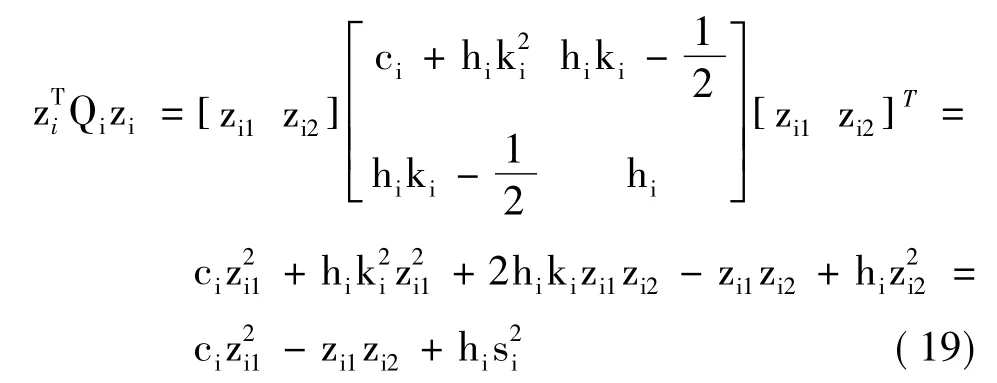
將式(19)代入式(17)得:

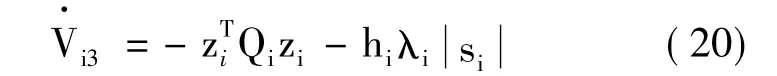
因為

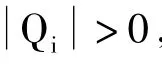
所以

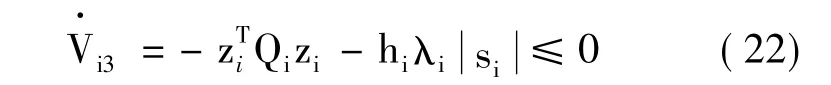
因此可知，系統在李亞普諾夫意義下是漸近穩定的。

由于UP=iq，所以同步控制系統的控制器輸出:

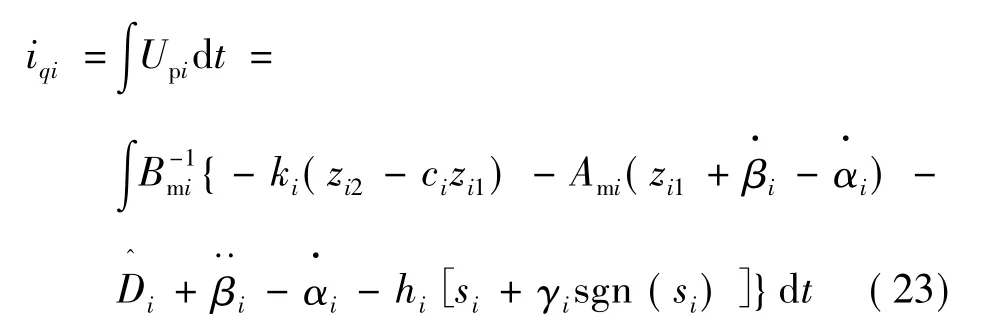
3仿真及分析

3．1仿真參數設置

為了驗證上述控制器的穩定性，以五臺永磁同步電動機的同步控制系統為例進行了仿真實驗。五臺電機模型在d-q旋轉坐標系下的各主要參數設置如表1所示，五臺電機的初始負載轉矩都是1 N·m，給定的參考速度 ω*(t)=41．9 rad/s，仿真時間 t=1．8 s，在 t=1．0 s時，五臺電機中的第 1、3、5這三臺電機的初始負載轉矩分別突變為2 N·m、4 N·m、6 N·m。由于 h、c、k 取值滿足式(21)，本文取 h=2 000，c=70，k=50，同時取 λ =30，γ =1．5。

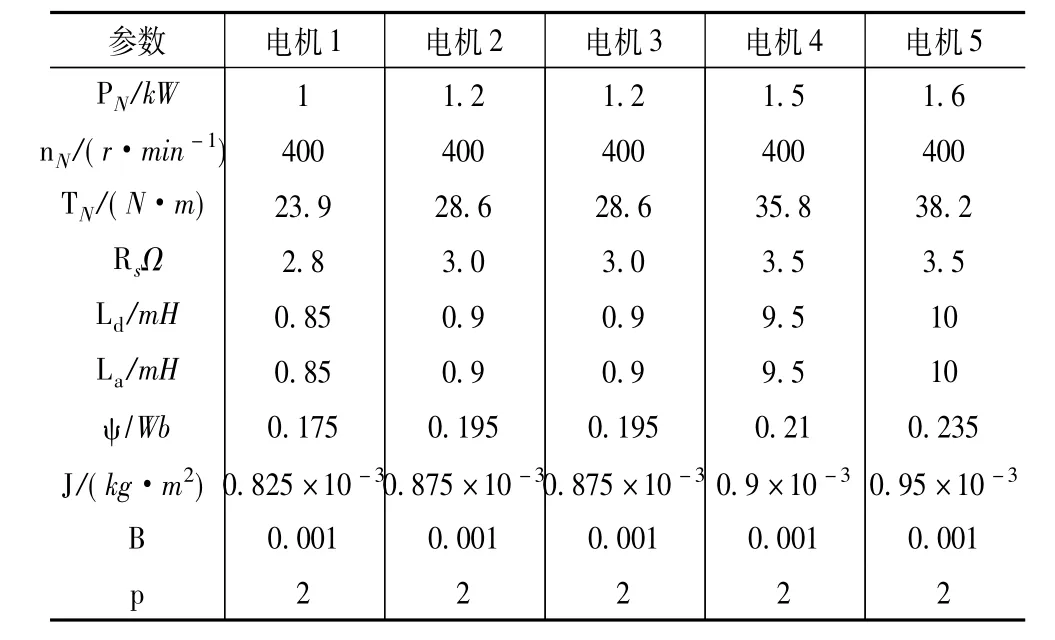
表1 五臺電機的參數設置

3．2 實驗結果

(1)實驗1

以五臺永磁同步電動機控制為例，選擇偏差耦合控制策略和主從控制策略進行仿真對比試驗，以證實偏差耦合控制策略的優越性。

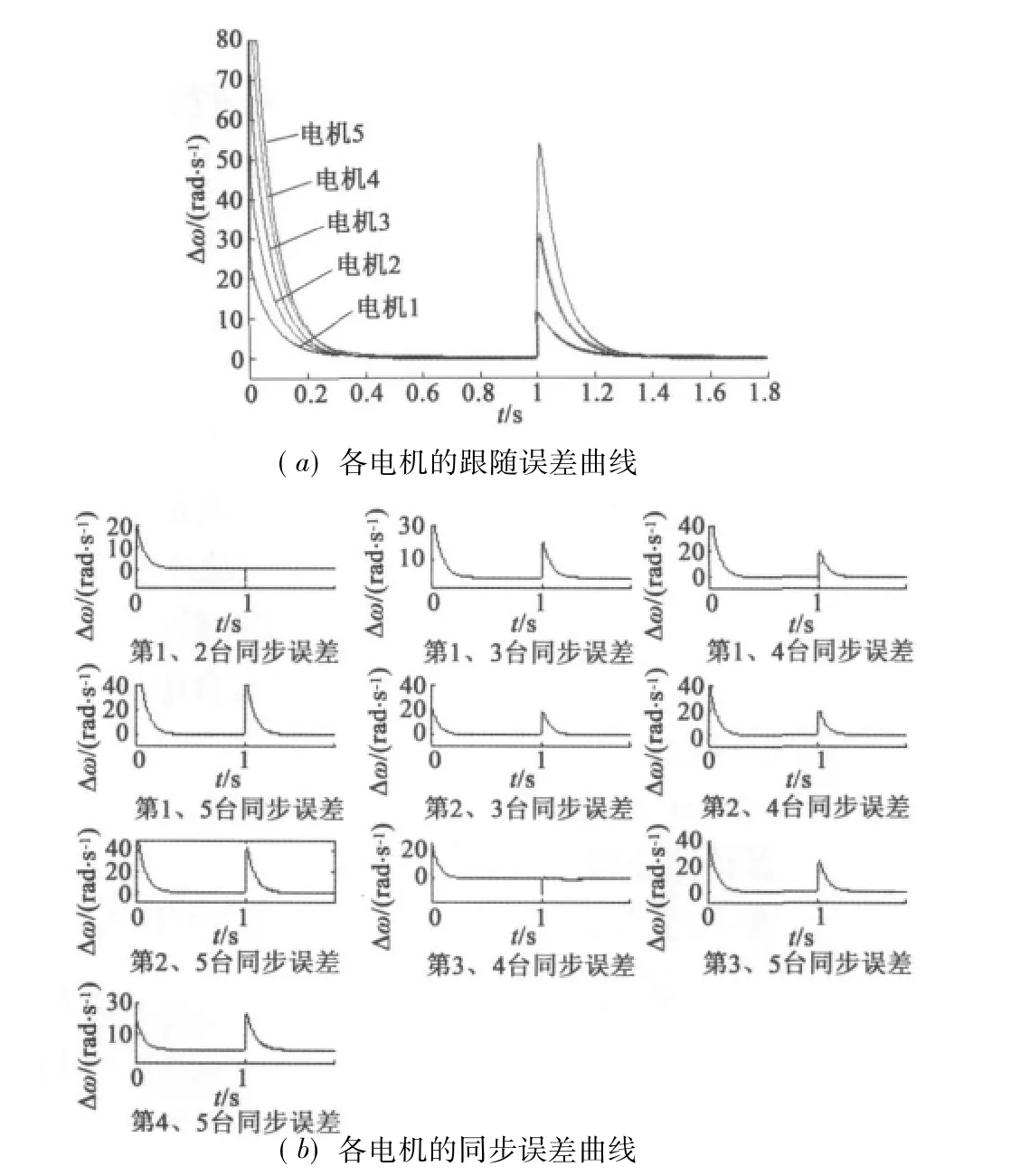
圖3 主從PID控制的跟隨和同步誤差曲線

采用主從控制策略和偏差耦合控制策略的PID同步控制跟蹤誤差及同步誤差仿真結果如圖3和圖4所示。由圖3可見，在電機起動時刻，偏差耦合控制的跟隨誤差小，并且跟隨誤差能夠同時近乎為零。在負載突變時，每臺電機的速度突變的范圍相對較小，同時每臺電機的速度突變之差也相對較小。此外，偏差耦合控制在初始時刻的同步誤差相對較小，并且能夠較快地達到穩態，在負載突變時，偏差耦合控制系統同步誤差也能夠保持在很小的范圍，而主從控制不相鄰電機的同步誤差很大。

(2)實驗2

采用偏差耦合策略，選擇基于反演的自適應滑模控制算法和PID控制算法進行仿真對比。在其他情況都相同時，上述兩個控制器的跟蹤誤差及同步誤差仿真結果圖4和圖5所示。從圖4可以得到，基于反演設計的自適應滑模控制在開始時刻能夠快速跟蹤目標速度。在負載突變時，能夠快速重新準確跟蹤目標速度，控制器表現出了很好的自適應性和魯棒性;同時，從圖5可以看出，基于反演設計的自適應滑模控制在開始及達到穩定時同步誤差都很小。在負載突變時，該系統的同步精度依然較高，體現了較好的抗干擾性。

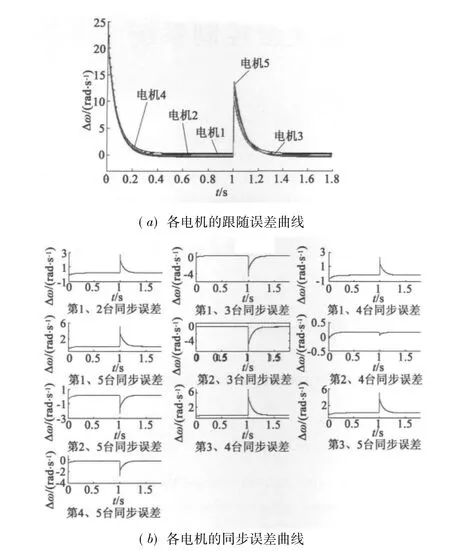
圖4 偏差耦合PID控制的跟隨誤差和同步誤差曲線

4結 語

本文針對多電動機系統所存在的負載擾動、參數變化等影響因素，采用偏差耦合控制策略，利用反演設計和滑模控制相結合，設計了一個多電動機同步控制系統，并進行了仿真對比。仿真結果表明該系統對負載擾動和參數變化帶來的影響具有較好的抑制作用，證明了該系統的具有較好的抗干擾性和魯棒性。

圖5 偏差耦合基于反演的自適應滑模控制的跟隨誤差和同步誤差曲線

［1］ 劉福才，王學蓮．多級電機傳動系統的同步控制理論與應用研究［J］．控制工程，2002，9(4):87-97．

［2］ 張承慧，石慶升，程金．一種基于相鄰耦合誤差的多電機同步控制策略［J］．中國電機工程學報，2007，27(15):59-63．

［3］ Koren Y．Cross-coupled biaxial computer controls for manufacturing systems［J］．Transaction of ASME，1980，102(4):265-272．

［4］ Francisco J，Ciro N，Ricardo A，et al．Comparison of multi-motor synchronization techniques［C］//Institute of Electrical and Electronics Engineers Computer Society．The 30th Annual Conference of the IEEE industrial Electronics Society，Busan，2004．NJ:IEEE，2004，2:1670—1675．

［5］ Perez-Pinal F J，Nunez C，Alvarez R．Compassion of multi-motorsynchronization techniques［C］//The 30th Annual Conference of me IEEE industrial Electronics Society．Busan，Korea，2004，10:2-6．

［6］ 高為炳．變結構控制的理論及設計方法［M］．北京:科學出版社，1996．

［7］ Taylor D G．Nonlinear control of electric machines:An verview［J］．IEEE Control Syst Mag(S0272—1708)，1994，14(6):41-51．

［8］ Perez-Pinal F J，Calderon G．Relative coupling strategy［C］//IEEE International Electric Machine and Drives Conference．2003，2(6):1162-1166．

［9］ 周國榮，李永豐．永磁同步電機的自適應滑模變結構控制［J］．控制工程，2009，16(1):49-51．