基于模型預測前饋的滾轉穩定伺服系統控制研究

許敘遙，林 輝

(西北工業大學院，陜西西安710072)

0引 言

滾轉穩定平臺是一種降低載體本身的滾轉角運動對其負載影響穩定裝置，主要應用于火箭彈、迫擊彈、巡航導彈上，用來搭載導航和制導設備。根據穩定方式不同，包括動力陀螺穩定、速率陀螺穩定［1-2］、半捷聯陀螺(導彈陀螺)穩定［3-4］以及地磁效應穩定［5-6］。目前上述幾種穩定方式的滾轉穩定平臺國外都已經成功應用于火箭彈、迫擊炮中，而國內在相關方面的研究起步較晚，有關的文獻和研究不多。

由于速率陀螺本身精度限制，基于速率陀螺穩定的滾轉穩定平臺對角度和速度控制精度要求很高。尤其是在載體滾轉速度急劇上升的時期，穩定平臺采用傳統PID控制器的控制精度難以令人滿意。

本文在對速率陀螺式滾轉穩定平臺進行詳細分析的基礎上，推導建立了穩定控制系統的傳遞函數模型。在此基礎上，設計了一種預測前饋復合控制器來提高穩定速度控制精度。最后采用DSP實現了預測前饋控制器并進行了驗證實驗。

1速率陀螺式滾轉穩定平臺原理

滾轉穩定伺服平臺的系統結構如圖1所示，伺服編碼器安裝于轉子的一端，用來測量伺服電機的轉子位置和速度信號，作為伺服電機控制的反饋信號。慣性陀螺安裝于電機轉子的另一端，用來測量穩定平臺的穩定角度和速度。而伺服控制系統根據慣性陀螺負載的反饋信號，控制伺服電機向載體滾轉相反方向旋轉，使慣性陀螺負載始終穩定在指定角度和速度范圍內，實現穩定目的。

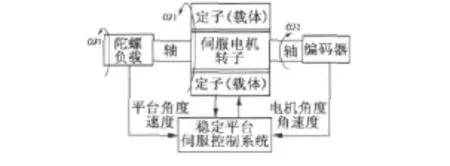
圖1 滾轉穩定平臺的系統結構圖

以大地為參照系，假設載體滾轉角速度為ω1;伺服電機旋轉角速度為ω2;穩定平臺的穩定速度ω3。根據牛頓第二定律有:

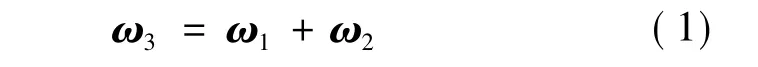
由于慣性陀螺角度和速度精度范圍限制，為保證陀螺的輸出不飽和，滾轉穩定平臺的伺服系統必須同時控制角度和速度。陀螺式滾轉穩定平臺選用永磁同步電動機作為伺服電機，其伺服電機控制原理如下:

在圖2中，采用id=0的矢量控制，矢量變換的角度來自于伺服編碼器的測量角度，而速度環和位置環以慣性陀螺測量裝置的信號作為反饋信號。

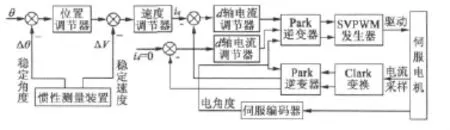
圖2 滾轉載體穩定平臺伺服控制原理圖

2伺服控制系統模型推導

永磁同步電動機以三相星型連接，假設:1)電機內磁路不飽和、電感不受電流變化的影響;2)忽略磁滯和渦流損耗;3)電機內磁場呈正弦分布在此假設條件下，則永磁同步電動機在d-q坐標系下的電壓方程:

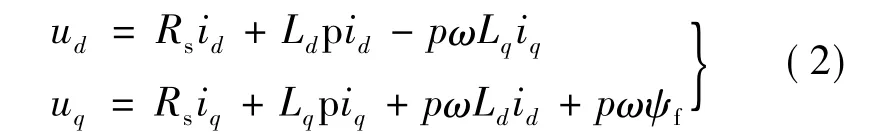
式中:Rs為繞組相電阻;Ld和Lq分別為d、q軸線圈的自感;p為微分算子;ud和uq分別為電壓在d軸和q軸的分量;id和iq分別為電流在d軸和q軸的分量;ω為機械角速度;ψf為電機的永磁磁通;p為電機極對數。

采用id=0控制，將式(2)化簡得到d-q坐標下電流的微分方程:

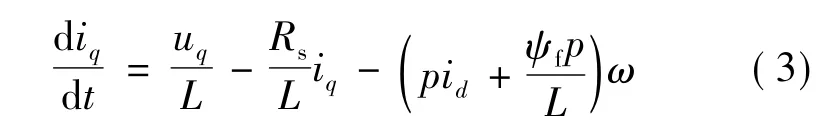
電機的電磁轉矩方程:

不計摩擦的電機運動方程:

式中:J為電機軸上的轉動總慣量;Te為輸出電磁轉矩。將式(3)～式(5)進行拉氏變換后整理得傳遞函數:

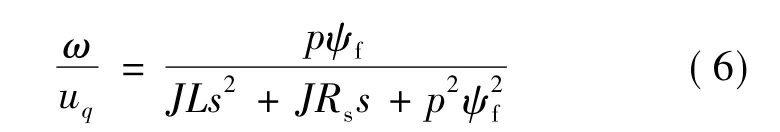
令ke=km=pmψf，永磁同步電動機采用電流反饋型脈寬調制逆變驅動，電流環采用PI控制器，得到永磁同步電動機電流環的模型框圖如圖3所示。

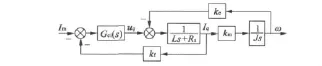
圖3 滾轉穩定平臺伺服系統電流環控制模型圖

圖中，Gci為伺服系統電流環的控制器傳遞函數;kf為電流的反饋傳遞系數;ke為電機的電勢系數;km為電機的力矩系數。

根據圖3，整個電流環傳遞函數:

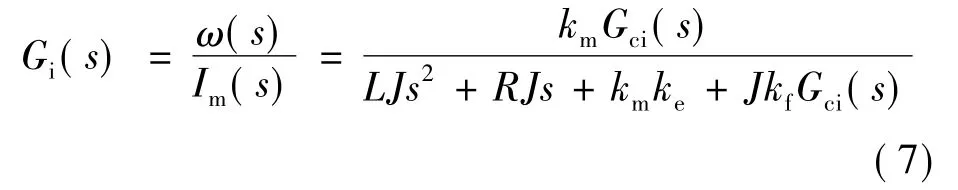
結合式(1)、圖2、圖3，整個滾轉穩定伺服系統控制框圖如圖4所示。

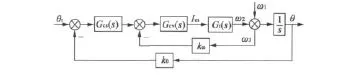
圖4 滾轉穩定平臺伺服控制系統框圖

圖中，kw為速度系數;kθ為角度系數;θr為輸入穩定角度，通常為零;Gcv(s)和Gcs(s)分別是速度控制器和位置控制器的傳遞函數，速度和位置控制通常采用PID控制。

從圖4可知，對滾轉穩定平臺的伺服系統來說，載體滾轉速度ω1為控制系統的擾動信號。當彈體靜止ω1等于零時，穩定平臺伺服系統就是通常意義上的位置伺服系統;當彈體滾轉ω1不為零時，穩定伺服系統是一個受載體滾轉速度干擾的控制系統，使用傳統PID控制不能很好抑制速度干擾，需要尋求新的控制方法來抑制系統干擾。

3預測前饋復合控制設計

在滾轉穩定平臺中，由式(1)可知，載體旋轉擾動速度ω1可以通過伺服編碼器和慣性陀螺測量速度計算得到，根據前饋復合控制理論，得到滾轉穩定平臺前饋復合控制系統框圖如圖5所示。

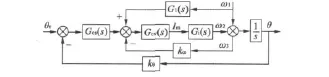
圖5 滾轉穩定平臺前饋復合控制系統框圖

根據全補償原則，滾轉穩定平臺擾動信號前饋通道傳遞函數:

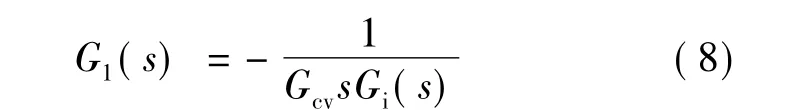
在實際系統中，式(8)控制器往往不能完全實現，通常采用靜態前饋的形式代替。由于滾轉穩定平臺對系統動態性能要求高，這種靜態前饋不能很好地適應系統動態性能的要求。這里考慮將模型預測控制跟前饋控制結合起來，用模型預測模塊來代替前饋通道傳遞函數的計算，這樣既能發揮前饋控制的優勢，又便于工程實現。

已知當前時刻可測干擾為ω1(k)，由于采樣頻率較快，假設預測l時刻內干擾保持不變，即有:

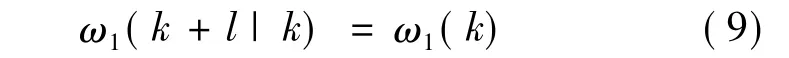
式中:ω1(k+l|k)表示由k時刻信息預測的k+l時刻速度干擾值。

當干擾輸入為零，角度參考信號為零，輸入階躍前饋控制u，根據圖5傳遞函數，由階躍響應模型可以測得前饋控制作用u對輸出的階躍θ的階躍響應系數，表示為 H={h1，h2，…，hn}，其中，N 為階躍響應的截斷時域長度。同理得到干擾ω1對輸出θ階躍響應系數，設 F={f1，f2，…，fn}。則可得干擾 ω1和前饋控制器輸出u，圖5對系統輸出角度ω1的影響可用下式表示:

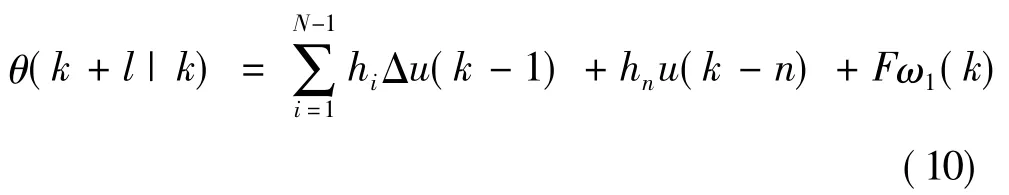
式中:Δ=-z-1表示差分算子，z-1為后移算子。預測控制的目的就是求取最優前饋控制作用u，使得式(10)達到最小值。將得到的最優控制作用u(k)作為前饋同道的輸出與反饋控制器輸出一起作用對象。在下一時刻，由測得的ω1(k+1)重新滾動計算最優控制作用，形成滑動優化預測控制。

由Garcia的動態矩陣控制器，綜上模型預測前饋控制器最終表述如下［7］:

性能指標函數:

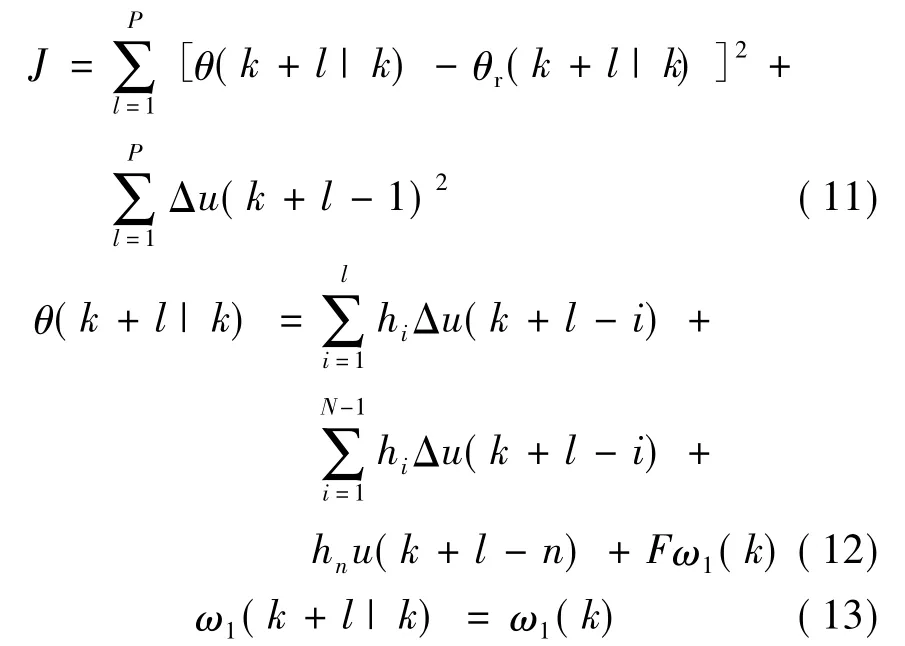
式中，θ(k+l|k)為當前k時刻的信息預測k+l時刻θ值;P為預測長度。經過對性能指標J求最小值，以及上述公式最優控制問題的滾動求解，得到前饋控制的控制輸出，對系統進行控制。

4實 驗

在實驗室建立滾轉穩定伺服試驗平臺，如圖6所示。

模擬電機帶動穩定伺服電機定子一起旋轉，用來模擬彈體滾轉角度和速度，模擬電機控制系統采用變頻器控制。而伺服電機軸的一端接有伺服編碼器，用來測量伺服電機轉子的角度，用于矢量控制變換角度;而慣性陀螺安裝于電機軸的另一端，用來測量滾轉穩定平臺輸出的角度和速度。

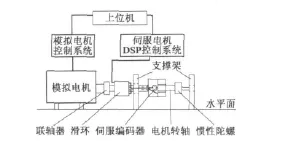
圖6 滾轉穩定平臺試驗系統示意圖

伺服電機控制系統是以 DSP芯片TMS320F2812為核心，構建了前述的基于空間矢量脈寬調制算法的位置、速度、電流三閉環控制系統，通過DSP編程實現上述前饋預測控制算法和PID控制器。

上位機通過模擬電機控制系統下載模擬曲線，通過變頻器控制模擬電機按照指定曲線運行，同時上位機還需要與DSP伺服控制系統通訊，實時接收、記錄以及顯示穩定平臺一些參數。

模擬電機主要電機參數如下:額定功率為3．7 kW，額定轉矩18 N·m，額定轉速為2 000 r/min，額定電流為8 A，該電機采用ABB公司的ACS800變頻器控制。伺服編碼器和模擬編碼器采用12位絕對式光電編碼器。

伺服永磁同步電動機參數如下:額定電壓U=27 V，額定電流I=3 A，定子相繞組 Rs=0．42 Ω，d、q軸相繞組電感Ld=Lq=0．45 mH，永磁磁通 φ=0．004 343 Wb，極對數 p=2。總轉動慣量 J=0．000 635 kg·m2;負載陀螺的最大速度輸出為300°/s。

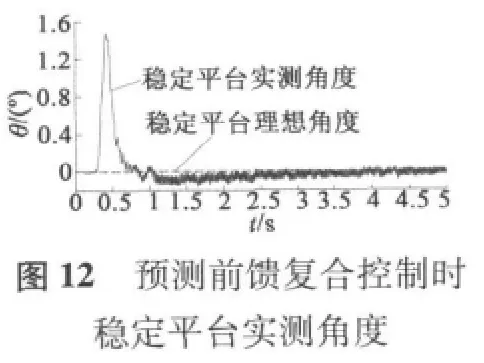
穩定平臺伺服系統分別采用純PID反饋控制和預測前饋PID反饋復合控制進行試驗，上位機以1 ms周期采集數據，最后用MATLAB將采集的數據進行繪圖如圖7～圖12所示。

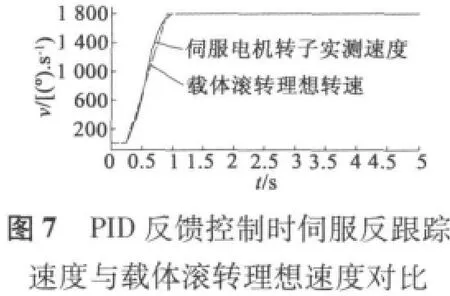
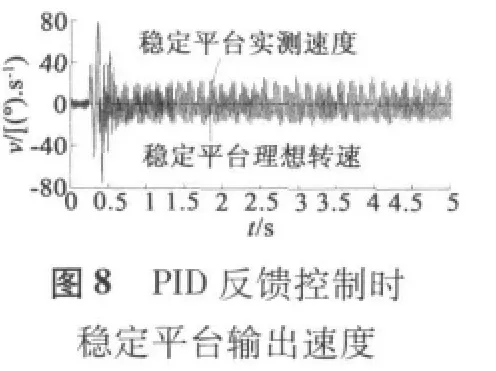
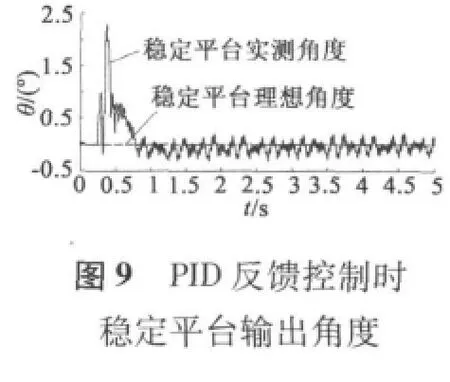
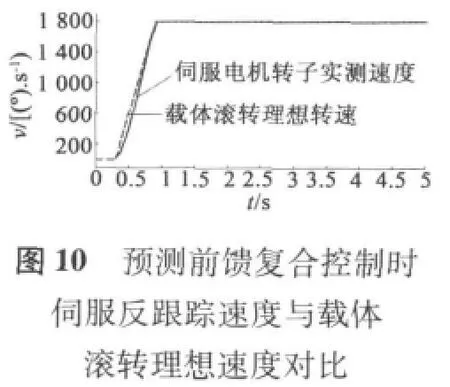
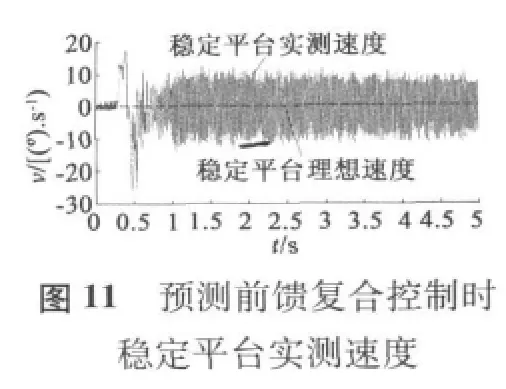
圖中，載體滾轉速度試驗曲線由兩部分組成，第一部分速度上升部分，大約0．7 s內速度從零提升到1 800 r/min，最大加速度大于 7 500°/s2，用來模擬彈體在彈膛點火彈體旋轉速度急劇增加的過程，這可以檢測穩定平臺伺服系統的動態性能。第二部分速度穩定運行部分，時間為4 s，載體滾轉速度穩定在1 800 r/min，用來模擬彈體在控制飛行過程，可以檢測穩定平臺的穩態性能。

從圖7至圖12看出，無論是PID反饋控制和預測前饋控制，在動態和穩定情況下，穩定平臺的穩定速度不超過80°/s，穩定平臺的穩定角度在2．5°以內，可看出慣性陀螺式穩定平臺精度較高。

載體滾轉速度動態上升階段，圖8顯示PID反饋控制下平臺的穩定速度最大為±80°/s內，圖9顯示對應的穩定角度最大為2．3°，圖11顯示預測前饋復合控制下平臺的穩定速度±25°/s，圖12顯示相應的穩定角度最大為1．5°;當載體滾轉速度穩定運行時，圖8顯示PID反饋控制下平臺的穩定速度最大為±20°/s內，圖9顯示對應的穩定角度為±0．3°，圖11顯示預測前饋復合控制下平臺的穩定速度±10°/s，圖12顯示相應的穩定角度最大為±0．1°。從上看出，預測前饋復合控制的控制精度比單純PID控制精度更高。

5結 語

試驗結果表明，無論單純PID控制還是預測前饋控制，陀螺式滾轉穩定平臺均能獲得較高的精度，這是由陀螺本身的高精度決定的。結果還顯示，本文提出的預測前饋復合控制能夠有效地提高系統的控制精度，大大改善系統的性能，且不影響系統的穩定性。

［1］ 張聘義，祁載康，崔瑩瑩．一種匹配濾波方法在導引頭捷聯穩定平臺中的應用研究［J］．紅外技術，2005，27(1):19-21．

［2］ Xu Xuyao，Lin Hui．Theory and Design of One-axis Stable Platform for Rotation［C］//ICEICE．Xi'an，China，2011:4691-4693．

［3］ 胡洋，彭曉樂，王宏宇．半捷聯式穩定平臺隔離度影響因素分析［J］．電子設計工程，2010，18(5):72-75．

［4］ 周瑞青，呂善偉，劉新華．彈載捷聯式天線平臺兩種穩定實現方法的比較［J］．系統工程與電子技術，2005，27(8):32-35．

［5］ 賀彤韡．彈載滾轉穩定平臺關鍵技術研究［D］．南京:南京理工大學碩士學位論文，2008．

［6］ 呂清利．圖像制導彈藥的彈載滾轉穩定平臺設計［D］．南京:南京理工大學碩士論文．2011．

［7］ Mayne D Q，Rawlings J B，Rao C V，et al．Constrained model predictive control:stability and optimality［J］．Automatica，2000(36):789-814．