發電機勵磁及SVC非線性最優協調控制

何振宇，李華強

(四川大學電氣信息學院智能電網四川省重點實驗室，四川成都 610065)

0 引言

電力系統的安全穩定是電力系統最重要的問題［1］。隨著電網規模的不斷擴大，超高壓、遠距離輸電線路日益增多，使得電力系統的穩定控制變得愈加復雜［2］。系統的穩定性包括功角穩定性和電壓穩定性。運行實踐和理論表明，在電力系統的重要樞紐點快速的提供動態電壓支撐是解決電力系統安全穩定的一個重要途徑［3－4］。如何在提高系統功角穩定性的同時，改善系統的電壓穩定性，是一個值得考慮的問題。

發電機勵磁系統對電力系統的動態行為有很大的影響，長期以來，人們對用發電機勵磁的控制來提高電力系統穩定性有深入的研究［5－9］。其附加控制即PSS對于增加系統阻尼、改善系統功角穩定性具有重要作用，但PSS對于改善系統的電壓穩定性作用不大，尤其對于一個遠距離輸電的系統。

柔性交流輸電系統(flexible AC transmission system，FACTS)元件的出現為解決電力系統的穩定控制問題提供了新的手段。FACTS家族的許多控制器，如靜止無功補償器(static var compensator，SVC)、可控串補(thyristor controlled series compensation，TCSC)以及靜止同步補償器(static synchronous compensator，STATCOM)等已成為提高系統暫態穩定的有效措施［10］。其中，SVC作為電力系統的動態電壓支撐的重要手段，越來越廣泛地應用于電力系統［11－13］。SVC具有突出的控制快速性，因此，深入研究SVC控制在改善電力系統穩定性中的作用具有重要意義。

與此同時，考慮到電力系統是一個強非線性系統，常規的控制器是根據某個運行點的線性化模型設計的，在大擾動的情況下可能無法發揮理想的控制效果。如何考慮電力系統的非線性特性，要求SVC與發電機勵磁系統進行協調控制以提高電力系統穩定，這已成為電力系統控制工作者研究的一個熱點問題。文獻［14］用反饋線性化技術對SVC與發電機勵磁協調非線性控制進行了研究。直接反饋線性化技術在處理系統的非線性問題時，沒有給出函數方程求逆的一般過程，在處理多輸入多輸出的復雜系統時較為困難。

微分幾何理論源自于20世紀80年代，近年來，近代微分幾何理論與非線性控制系統相結合，形成了一門新的學科體系，即非線性系統幾何理論。微分幾何理論結合現代控制理論在電力系統控制技術中得到了很好的應用。被用于解決大型發電機的勵磁控制、無功補償的非線性控制等，得到了比較好的控制效果。

采用微分幾何反饋線性化理論設計SVC控制器，并與發電機勵磁系統進行協調控制，結合現代控制理論，設計了發電機勵磁和SVC系統的最優控制規律，使得控制器可以同時滿足發電機功角穩定和SVC接入點電壓穩定兩個目標。仿真結果證明了控制規律的有效性。

1 微分幾何狀態反饋線性化理論簡述

考慮到文中的情況，針對一個雙輸入雙輸出的仿射非線性系統。其一般形式如下。

其中，X是n維狀態向量;f(X)及g1(X)、g2(X)均是n維向量場;u1、u2是n維控制變量;y1(t)、y2(t)是輸出變量;h1(X)、h2(X)是X的標量函數。

根據微分幾何理論，對于每一個輸出量yi，有一個對應的關系度ri，則多變量系統的關系度r是一個集合。對于文中的系統，假定有r=r1+r2=n，n是狀態向量維數。若非線性系統(1)能被輸入狀態反饋線性化，則在一個鄰域Ω內存在一個微分同胚T，做坐標變換，系統(1)變換成。

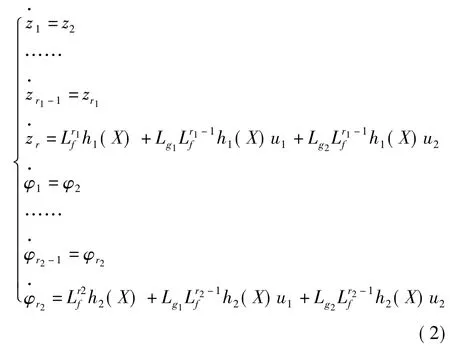
即可轉化為以新坐標系表達的標準型。

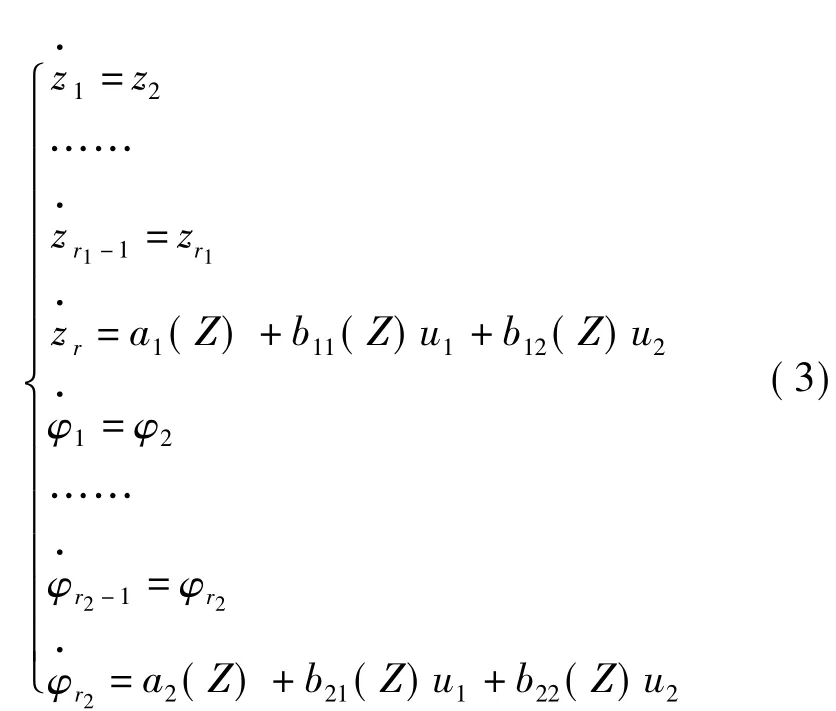
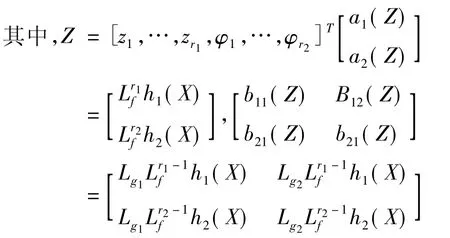
在新坐標下，系統是一個線性系統，可以利用成熟的線性控制理論來設計控制器。

微分幾何反饋線性化數學概念清晰，是一種精確的線性化方法，數學變換理論嚴格，經證明，經過微分幾何線性化后的系統的能控性、能觀性都不發生改變，是一種優秀的非線性控制理論。

2 系統數學模型

2.1 系統接線方式

考慮最典型的單機遠距離與無窮大電網互聯的系統如圖1所示。

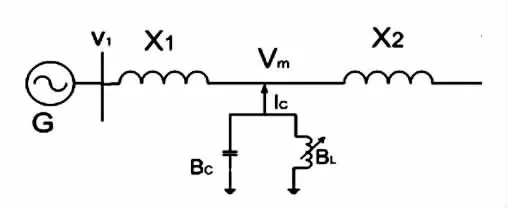
圖1 具有SVC的單機無窮大系統

2.2 發電機模型

對于單機無窮大系統，發電機模型可描述為

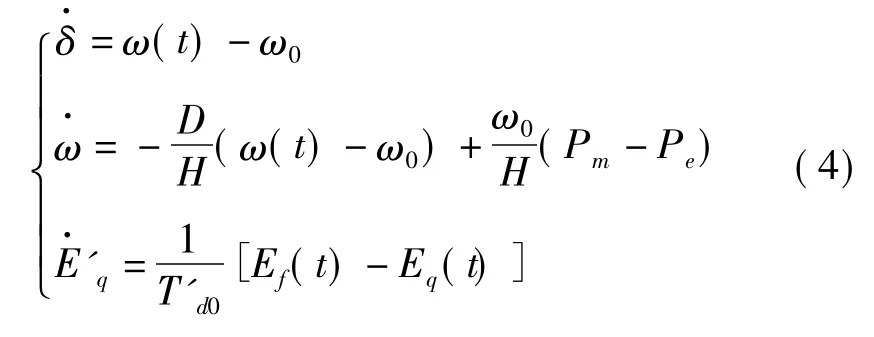
且有

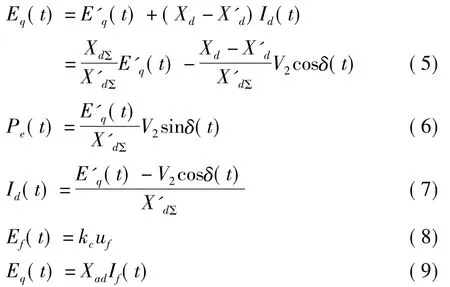
式中，Id(t)是發電機直軸電流;If(t)是勵磁電流;uf是勵磁電壓;Xad為定子繞組與勵磁繞組的互感抗，XdΣ=Xd+X1，X'dΣ=XdΣ=X'd+X1，X1=X'd+X1+X2+(X'd+X1)·X2·Bsvc;Xd和X'd分別是發電機的直軸電抗和暫態電抗;E'q(t)為發電機交軸暫態電勢;δ為發電機相對無窮大母線的功角;Bsvc是SVC的等值電納。

2.3 SVC 模型

SVC采用如圖2所示的實用模型。

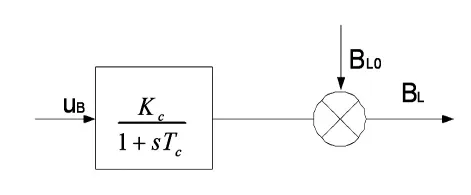
圖2 SVC模型

其動態數學模型為

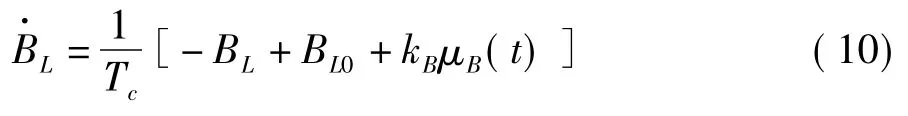
式中，Tc是SVC控制器的時間常數;BL為SVC中電感支路電納;BL0是初始值;kB是控制器增益;μB為控制器輸入。

為了簡化設計，一般假定如下。

(1)發電機采用三階模型。

(2)不考慮勵磁系統的動態過程，即Ef=VR，Ef是勵磁系統的輸出電壓(輸入)，VR是勵磁系統的控制電壓(輸入)。

(3)發電機的機械功率在暫態過程中保持不變。

基于以上假設，單機無窮大系統結合SVC的數學模型，便得到帶有SVC的系統模型，控制目標是要同時滿足發電機功角穩定和SVC處電壓穩定兩個目標，因此選取功角偏差和電壓偏差作為輸出量。寫成狀態空間形式為

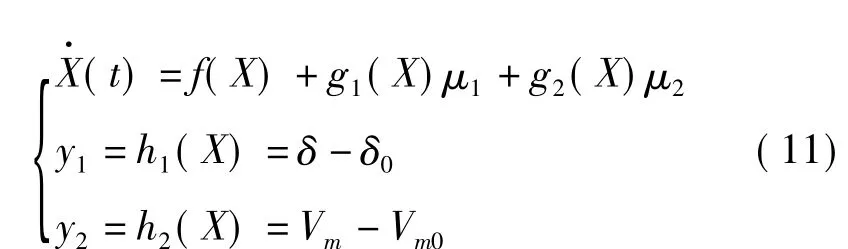
Vm為SVC接入點的等效電壓;Vm0是其穩態值。又根據SVC電路特性有:是可調電感支路電流。

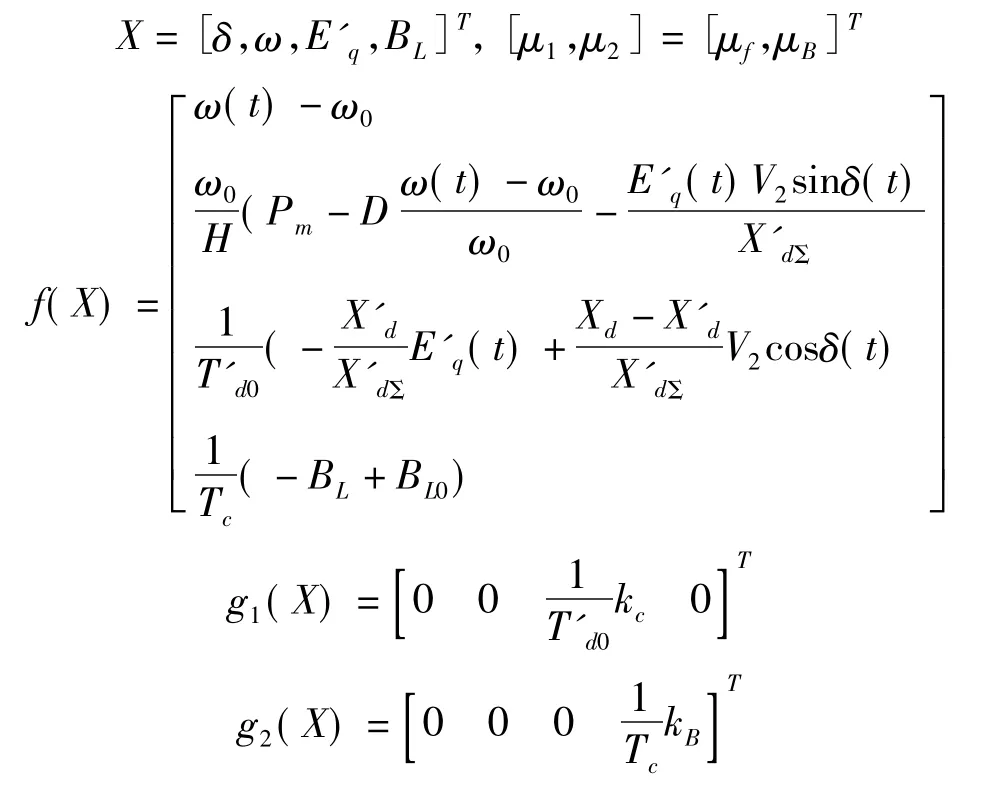
3 基于微分幾何反饋線性化的控制器設計

對于所提的仿射非線性系統，首先驗證其是否能進行精確線性化，為此需求解其對兩個輸出y1=h1(X)、y2=h2(X)的關系度 r1、r2。對于 y1=h1(X)有

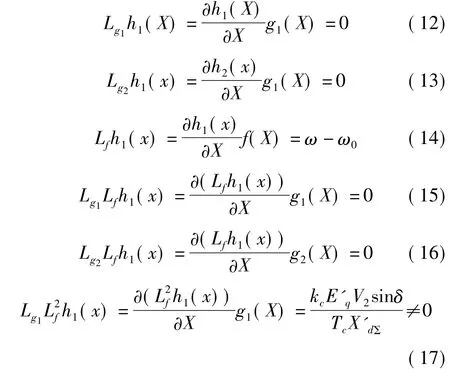
由此可知r1=3。對于y1=h2(X)有

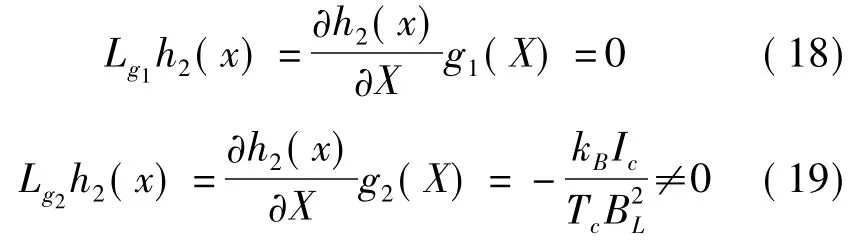
可知r2=1。則有r=r1+r2=n=4。滿足系統被線性化的條件，因此，存在一個坐標變換使得系統被新坐標下線性化。

選擇如下的坐標變換。

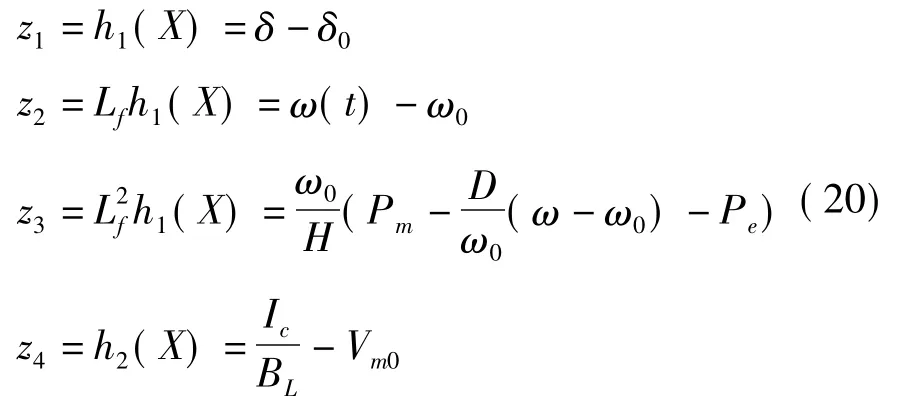
其雅各比矩陣為

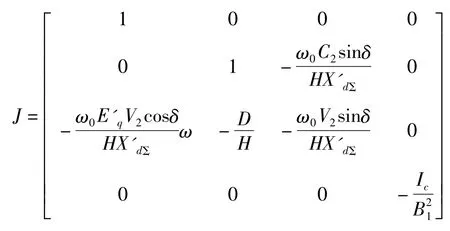
在系統運行范圍內，矩陣的行列式值不為0，由此可知該坐標變換是一組合格的坐標變換。對于新坐標下的系統有

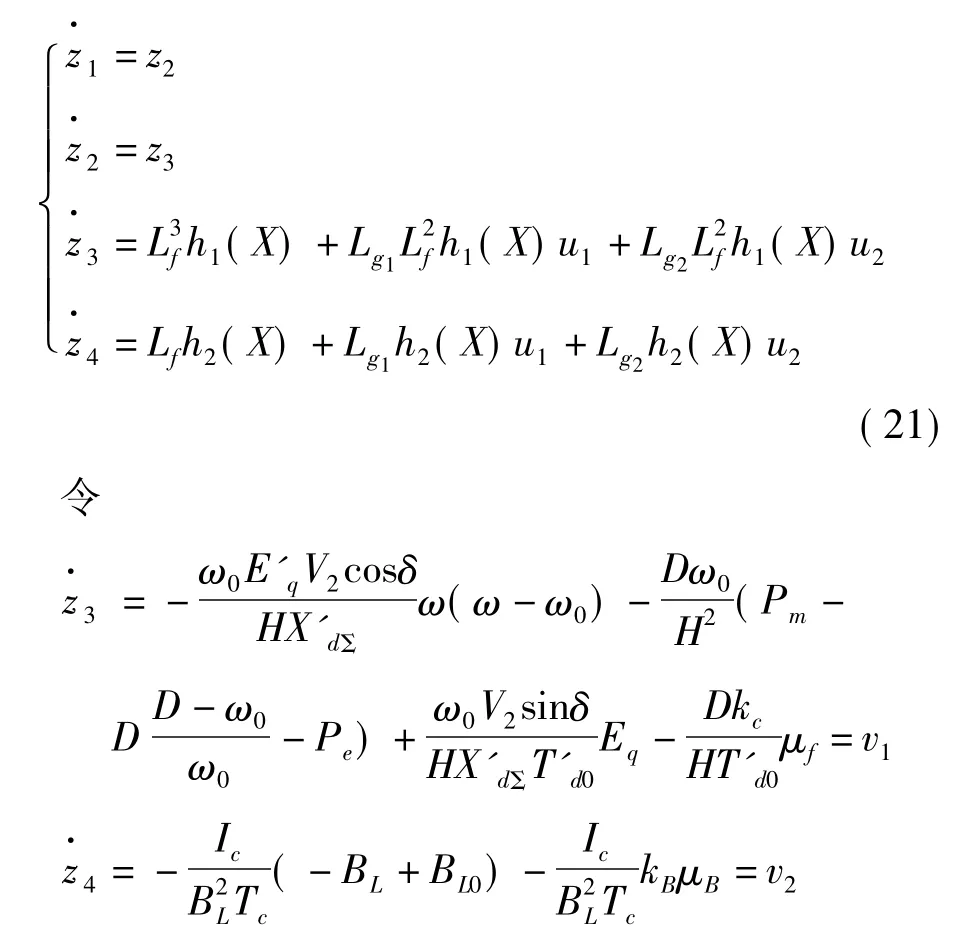
得到線性化方程

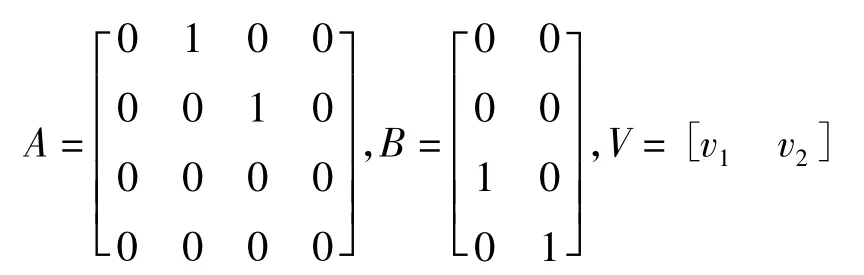
輸出方程

求解 u1、u2得

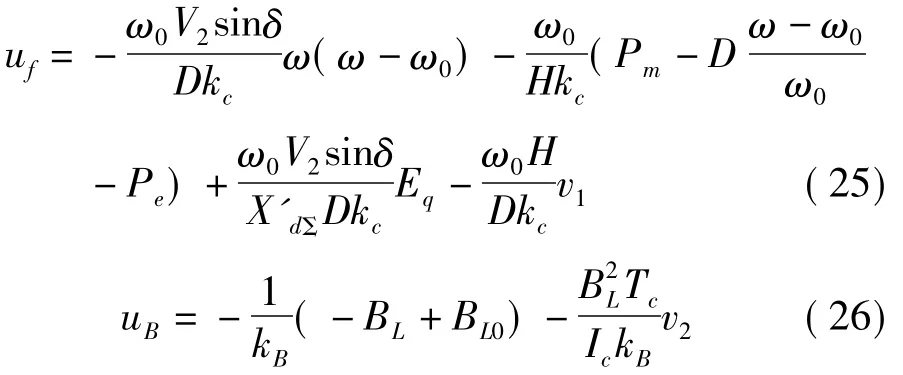
V= －R－1BTPZ= －KZ，其中，P是 Riccati方程ATP+PA－PBR－1BTP+Q=0的對稱正解。對于系統，選取合適的權矩陣，求得最優反饋增益系數為

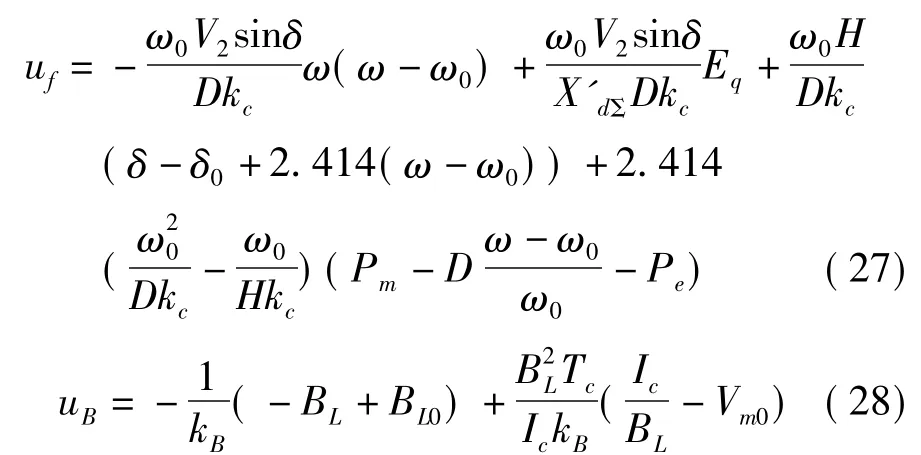
從控制規律可以看出，發電機勵磁系統和SVC均實現了本地信號控制，因此所設計的控制器具有分散協調性，而無需要信號的通信，減少了由于信號延遲等引起的誤差。

4 仿真分析

利用電磁暫態仿真軟件PSCAD/EMTDC對圖1所示的單機無窮大系統進行仿真。SVC接在長距離輸電線路的中點，系統參數如下。

Xd=1.854 8，X'd=0.256 8，X1=X2=0.034 3，H=8 s，T'd0=9.22 s，Tc=0.1 s，發電機容量 350 MW，功率因數0.9，故障設置分為兩種:(1)1.0 s時發電機出口三相接地短路，持續時間0.1 s。(2)1.5 s時線路中點發生三相接地短路，持續時間0.1 s。發電機功角曲線及SVC接入點電壓曲線如圖5所示。圖3、圖4表示故障1的情況，圖5、圖2表示故障2的情況。

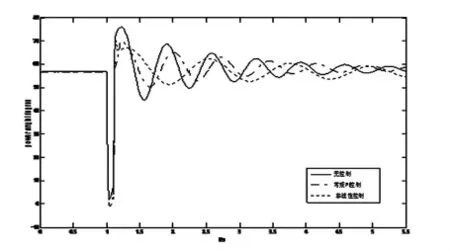
圖3 機端故障發電機功角

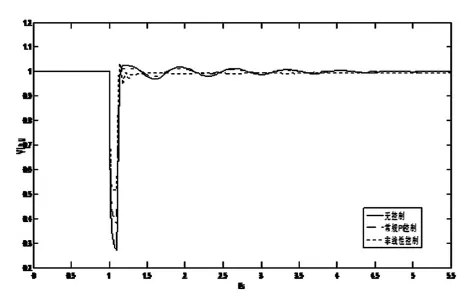
圖4 機端故障電壓曲線

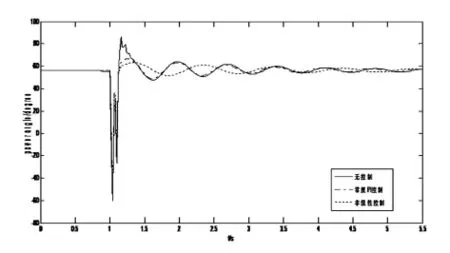
圖5 中點故障功角曲線

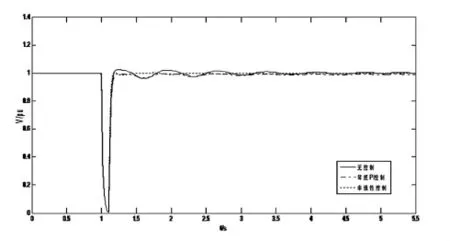
圖6 中點故障電壓曲線

由圖可知，系統加裝控制器后，發電機功角振蕩和SVC接入點的電壓波動都能很快平息，系統的暫態穩定性和電壓穩定性都得以提高，較常規的PI控制器效果要好。

5 結語

電力系統是一個強非線性系統，針對所提的單機無窮大系統，通過微分幾何反饋線性化理論，結合最優控制方法，在保留系統的非線性特性的情況下，設計了一種發電機勵磁系統和SVC非線性協調最優控制規律。仿真驗證了控制規律能有效提高系統的功角穩定性和電壓穩定性，提出的方法都能夠保證系統的穩定性，且控制規律實現了本地信號控制。

利用非線性理論設計的控制器能明顯地提高電力系統暫態穩定性和電壓穩定性。微分幾何反饋線性化的數學理論基礎堅實，但也有無法克服的缺點，如:要求系統的數學模型精確，不具備對模型和參數不確定的魯棒性，數學推導及控制規律非常復雜等。這都是以后研究將要注意的地方。

［1]柯寧，蘇建設，陳陳.TCSC與SVC用于提高輸電系統暫態穩定性的仿真研究［J］.電力系統自動化，2004，28(1):20－24.

［2]蘭 洲，倪以信，等.現代電力系統暫態穩定控制研究綜述［J］.電網技術，2005，29(15):40 －50.

［3]陳閩江，王杰，等.含STATCOM多機系統的廣義Hamilton非線性控制設計［J］.高電壓技術，2010，36(7):1833－1838.

［4]廖民傳，蔡廣林，張勇軍.交直流混合系統受端電網暫態電壓穩定分析［J］.電力系統保護與控制，2009，37(10):1－4.

［5]張帆，徐政.勵磁系統及電力系統穩定器對發電機組次同步諧振阻尼特性的影響［J］.電網技術，2006，306(18):14－18.

［6]梅生偉，黎雄，盧強，等.基于反饋線性化方法的勵磁系統非線性H∞控制研究［J］.電力系統及其自動化學報，1999，11(4):1 －7.

［7]劉輝，李嘯驄，韋化.基于目標全息反饋法的發電機非線性勵磁控制設計［J］.中國電機工程學報，2007，27(1):14－18.

［8]Lu Q，Sun Y，Xu Z，etal.Decentralized Nonlinear Optimal Excitation Control［J］.IEEE Transactions on Power Systems，1996，11(4):1957 －1962.

［9]鮮艷霞，李興源.提高暫態穩定性的HVDC與發電機勵磁的非線性最優協調［J］.繼電器，2004，32(20):1 －4.

［10]王寶華，楊成梧.FACTS穩定控制策略綜述［J］.電力自動化設備，2000，20(2):15 －21.

［11]楊波，劉天琪，李興源，等.基于最優變目標的HVDC與SVC非線性綜合協調控制［J］.繼電器，2006，34(17):29－33.

［12]嚴偉佳，蔣平.抑制區域間低頻振蕩的FACTS阻尼控制［J］.高電壓技術，2007，33(1):189－192.

［13]D.Z.Fang，Xiondong Yang，T.S.Chung，et al.Adaptiv Fuzzy－logic SVC Damping Controller Using Strategy of Oscillation Energy Descent［J］.IEEE Transactions of Power System，2004，19(3):1414－1421.

［14]馬幼捷.SVC與發電機勵磁協調非線性控制［J］.電工技術學報，1998，13(4):1－4.