改進的OPAST算法及其在盲多用戶檢測中的應用

王 豪，張 捷，任松育

（西北工業大學 電子信息學院，陜西 西安 710129）

子空間分解是自適應陣列信號處理的重要工具，它廣泛應用于數據壓縮，系統鑒定，數據濾波，參數估計，模式識別等領域。在基于智能天線的DOA估計中也有重要的應用[1]，基于子空間的高分辨的方法已經成功地運用于時間上的和空間上的主譜分析，典型例子如：多重信號分類（MUSIC），最小模估計方法，旋轉子空間（ESPRIT）估計，加權子空間擬合（WSF），基于KL變換的數據壓縮等。近年來，子空間跟蹤的方法得到了迅速發展，大致可以分為3類：1）對ED/SVD進行改進；2）秩 1擾動更新方法的變形；3）將 ED/SVD看成是最優化問題。Bin.Yang提出的PAST算法屬于第3類，是其中魯棒性和有效性最好的方法之一[2]，然而在某些情況下，PAST算法不收斂，針對這一問題，K.Abed-meraim等提出了正交的PAST（OPAST）算法，它保證了權向量在每次迭代的正交性，并具有和PAST算法一樣的線性復雜度，和自然冪法[3]一樣的全局收斂性。

OPAST算法與ED/SVD算法相比具有較低的計算復雜度，以及它自身的自適應性，使它更適用于實時信號處理。多用檢測技術是3G以及4G的關鍵技術，盲多用戶檢測[4]是多用戶檢測中的一種，它僅僅利用特征波形先驗知識和感興趣用的用戶定時模式來檢測用戶信息，是目前多用戶檢測的主要發展方向。文中將OPAST算法應用于盲多用戶檢測中，通過仿真實驗發現，在迭代一定次數后，會出現誤碼率變大的現象，為了解決這一問題，文中提出了一種方法，并通過仿真實驗得以證明。

1 信號模型與子空間分解

對于一個具有K個用戶的同步DS-CDMA通信系統[5]，在具有高斯白噪聲的信道中，經過碼片匹配濾波器和碼片速率采樣后，在一個符號間隔內，接收端的輸出樣本為一個N維向量：

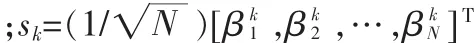
為了方便和不失一般性，假設K個用戶的擴頻碼都是線性獨立的。 記：S=[s1，s2，…，sK]，接收數據的自相關矩陣為：

對矩陣Cr進行特征值分解：

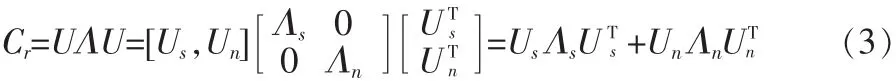
其中：U=[Us，Un]；Λ=diag（Λs，Λn）；Λs=diag（λ1，λ2，…，λK）含有 Cr的 K 個最大的特征值；Us=[u1，u2，…，uK]中為相應的正交特征向量；Λn=diag（λK+1，λK+2，…，λN）中為相應的正交特征向量。 range（Us）為信號子空間，它的正交部分range（Un）為噪聲子空間。其中Us和Un都是酉矩陣。

2 OPAST算法

B.Yang提出的投影近似子空間跟蹤算法 （簡稱PAST）的思路是把信號子空間的跟蹤轉化為非約束最小化問題。它通過預測逼近將最小化問題簡化為指數加權最小二乘問題。它是所有子空間跟蹤算法中健壯性最好，效率最高的算法之一，計算復雜度為O（nr），其中n為向量序列的維數，r為子空間的維數。

r表示n×1隨機向量，令C=E{rrT}為r自相關矩陣，目標函數定義為

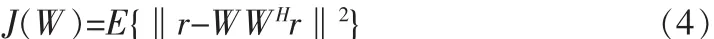
目標函數可以用跡函數表示如下：

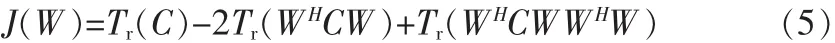
式中，W是n×r矩陣，假設其秩等于r，Tr（）表示矩陣的跡。

下面考慮極小化問題min J（W）。與之相關的重要問題是：

1）是否存在J（W）的全局極小點W？

2）該極小點W與自相關矩陣C的信號子空間有何關系？

3）是否存在J（W）的其他局部極小點？

Yang證明了下面的定理[6]：

定理1 W是J（W）的一個平穩點，當且僅當W=UrQ，其中Ur∈Cn×r有自相關矩陣C的r個不同的特征向量組成并且Q∈Cr×r為任意酉矩陣（酉矩陣即復數域的正交矩陣）。在每一個平衡點，目標函數J（W）的值等于不在Ur的那些特征值之和。

定理2 目標函數J（W）的所有平穩點都是鞍點，除非Cr由自相關矩陣C的r個主特征向量組成。在這一特殊情況下，J（W）達到全局最小。

在某些情況下，PAST算法沒有收斂性，為了減輕這一缺陷，更重要的是為了保證在每次迭代時，權向量的規范正交性，K.Abed-Meraim等人提出了一種新的方法：OPAST（Orthonormal PAST）。 OPAST算法和PAST算法有一樣的線性復雜度O（nr），n為向量序列的維數，r為主子空間的維數。OPAST算法還具有規范正交性和全局收斂性。

OPAST算法在PAST算法的基礎上，在每次迭代時對權重向量做規范正交的處理：

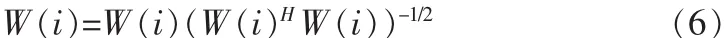
（由于W（i）HW（i）=I，所以上式成立）。

其中，（W（i）HW（i））-1/2指的是W（i）HW（i）=I的逆的平方根。為了計算后者，使用W（i）的迭代方程，此時W（i-1）已經是規范正交矩陣：

由式子（6）和（10），以及W（i）的迭代公式得：

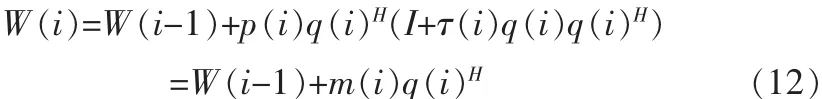
其中：

因此OPAST算法可以寫成如下形式：

選擇初始化W（0）和Z（0），以及β

3 基于OPAST算法的盲多用戶檢測

假設待檢測用戶為用戶1，一個線性MMSE檢測器，解調第1個用戶數據的解調向量為w，則判決器的輸出為

其中：w∈RN。在約束條件wTs1=1下，最小化MSE（w ）=E（（A1b1-wTr）2），用信號子空間參數表示可得到（4）式中的MMSE檢測器w為

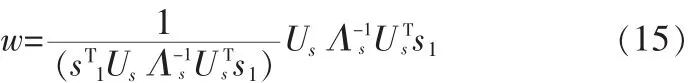
這里要計算w，需要知道Us、Λs，然而OPAST算法只能計算Us，要想把OPAST算法應用于盲多用戶檢測中，需要進行數據壓縮操作。經數據壓縮后，w為如下形式：

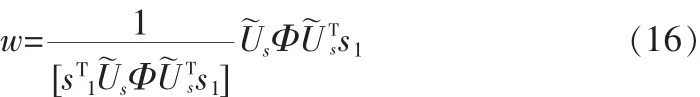
基于OPAST的盲多用戶檢測算法的步驟如下：

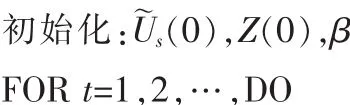
4 仿真實驗及改進的OPAST算法

對于一個具有高斯白噪聲的DS-CDMA系統，用戶數為8，目標用戶為用戶1，其余用戶為干擾用戶，每個用戶的采用31位的Gold擴頻碼，目標用戶的信噪比為25 dB，目標用戶的功率為1，干擾用戶的功率相同。

將OPAST算法應用于多用戶檢測中，發現在迭代5 000次左右時，會出現誤碼積累的現象，誤碼率會突然上升（如圖1所示）。究其原因，OPAST算法中要求Z（i）是求逆后的對角元素表示信號子空間的K個最大的特征值，其初始值為Hermitian正定矩陣，仿真實驗中，以實信號為例，故Z（i）為實對稱正定矩陣。在計算過程中由于誤差的存在，使求出的Z（i）不滿足實對稱正定的性質，從而導致了在迭代若干次后誤碼率增大的現象。

圖1 改進前的OPAST算法的berFig.1 Ber of unimproved OPAST algorithm

為了解決這一問題，文中提出將求出的Z（i）的上三角和下三角相加除以2得到上三角，再將上三角賦值給下三角的方法，仿真結果如圖2所示，這種方法有效地解決了上述問題。通過將上下三角部分加權求平均值，可以有效地減小由只算上三角部分或只算下三角部分所帶來的誤差。

圖3所示結果為改進前和改進后的OPAST算法的sinr比較，兩者基本相當，表明改進后的OPAST的sinr性能沒有下降；圖4為改進后的OPAST算法與PAST算法的比較，OPAST算法要在sinr性能方面優于OPAST算法。

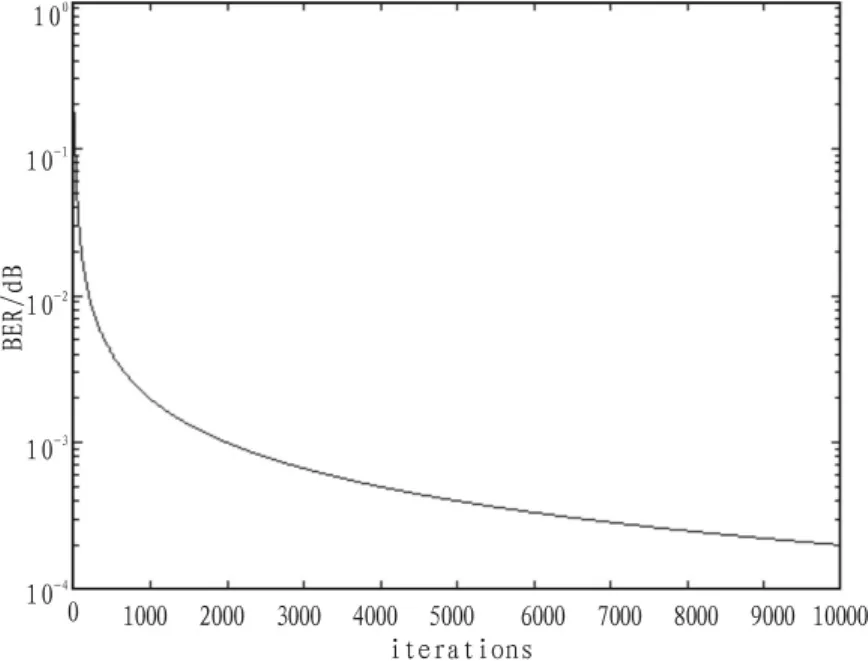
圖2 改進后的OPAST算法的berFig.2 Ber of improved OPAST algorithm

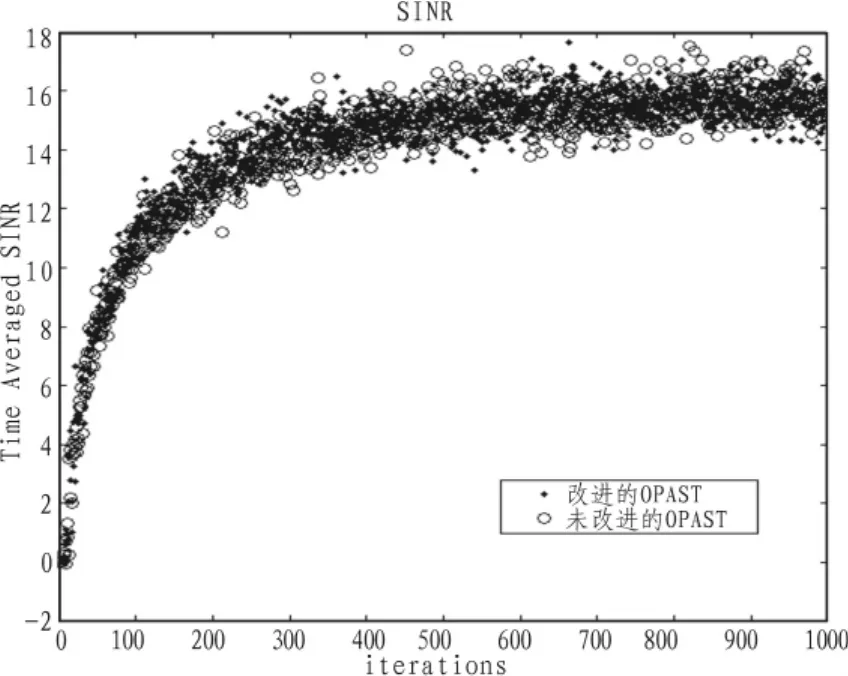
圖3 改進前和改進后的OPAST的sinrFig.3 Sinr of unimproved and improved OPAST

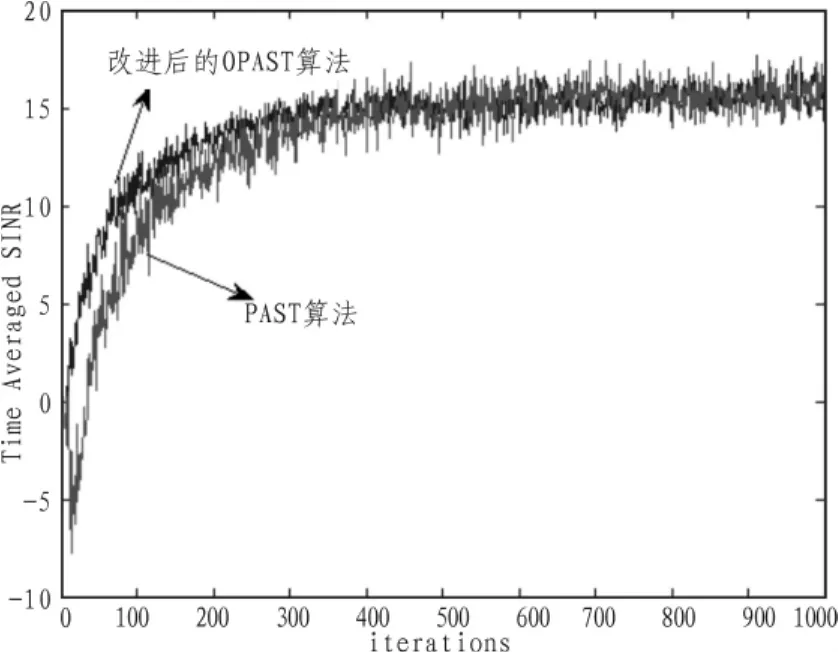
圖4 改進后的OPAST算法與PAST的sinr比較Fig.4 Sinr of improved OPSAT and PAST

5 結束語

文中提出的改進的OPAST算法，解決了誤碼率在迭代一定次數后上升的問題，誤碼率性能得到提升，信號干擾噪聲比性能與改進前相比基本不變，經過改進后的OPAST算法將更適應于實時信號處理。

現在的子空間跟蹤算法，普遍只能跟蹤信號子空間，而不能跟蹤特征值，使用ED/SVD方法可以得到特征值和特征向量，但其計算復雜度太大，不適合實時信號處理，且不具備自適應性。對既可以跟蹤特征值又可以跟蹤特征向量的子空間跟蹤方法的研究將成為今后的熱點。

[1]錢林杰，程翥，石斌斌，等.一類子空間跟蹤方法的改進[J].信息處理，2010（5）：741-745.

QIAN Lin-jie，CHENG Zhu，SHI Bin-bin，et al.Improvement of a kind of subspace tracking methods[J].Information Processing，2010（5）：741-745.

[2]Yang B.Projection approximation subspace tracking[J].IEEE Trans Signal Processing，1995（44）：95-107.

[3]HUA Y，CHEN T，MIAO Y.A unifying view of a class of subspace tracking methods[J].In ISSPR’98，1998（2）：27-32.

[4]馬建倉.盲信號處理[M].北京：國防工業出版社，2006.

[5]Wang X，Poor H V.Blind multiuser detection：A subspace approach[J].IEEE Trans.Inform.Theory，1998，44（2）：667-691.

[6]Yang B.Projection approximation subspace tracking[J].IEEE Trans Signal Processing，1995（43）：95-107.