導彈發射箱結構優化設計

張 劍

(中國空空導彈研究院，河南 洛陽 471009)

在導彈箱式發射技術中，國外已經做到了發射箱的輕型化和小型化，美國和俄羅斯的彈箱質量比一般可以達到3:1左右，處于世界先進水平［1］。而在國內，發射裝置的設計普遍采用傳統設計方法，設計者往往是根據設計要求和實踐經驗，參考類似發射箱結構，通過判斷去創造設計方案，然后進行強度、剛度、穩定性等各方面的計算校核，以證實設計方案的可行性［2］。這是一種人工試湊和定性分析比較的過程，主要的工作是發射箱性能的重復分析，缺乏集成優化，既要花費大量的時間，最終得到的設計方案又往往不是最優的方案，因此發射箱的質量通常都比較大，與國外差距非常明顯。以我國采用箱式發射的某些巡航導彈為例，貯運發射箱的質量與導彈接近甚至超過導彈的質量。如何降低導彈發射裝置的質量，實現發射系統的輕量化是一個亟待解決的問題。本文嘗試將結構優化設計的方法引入到導彈發射系統的分析研究中，結合工程結構優化設計理論、有限元方法、發射動力學和結構力學理論，進行發射箱的結構優化設計，以期得到滿足強度、剛度和結構穩定性要求，同時具有較輕質量的發射箱的一組結構參數，旨在探討一種導彈發射裝置減重的方法和途徑，能夠對發射系統的輕型化設計提供一定的參考價值。

1 發射箱結構有限元分析

1.1 發射箱結構分析

本文的研究對象是某型地空導彈的貯運發射箱，導向方式為導軌式，斷面為矩形。發射箱結構主要由箱體、加強筋和其他一些小型配件構成，為了便于進行有限元分析和優化處理，對發射箱的結構進行了簡化，略去對整體結構屬性影響不大的一些小的部件以及箱體上的孔洞結構。簡化后的發射箱結構主要由橫截面為矩形的薄壁箱體和多條環形加強筋組成，如圖1 所示。

圖1 簡化的發射箱結構

1.2 發射箱受力分析

在發射過程中，發射箱受力情況是比較復雜的，且隨時間不斷變化。下面簡要介紹發射箱的受力情況及其在有限元分析時的處理方法:

1)在對發射箱進行有限元分析時，把發射系統其他部分當做剛體來處理，其實相當于把發射箱在耳軸處固定，又考慮到實際情況中允許發射箱在后耳軸處有微小的轉動，在前耳軸處有微小的移動，于是在實際的有限元分析計算時去除這兩個自由度約束;

2)由于是單獨地對發射箱進行優化分析，所以要考慮到導彈通過導軌對發射箱箱壁施加的作用力。實際計算時，將導軌對發射箱的作用力施加到導軌與箱壁的接觸面積上。

3)在實際中燃氣流載荷對發射箱的作用相當復雜，但經過簡化后，沿導彈軸向的作用力要遠遠大于其他方向，于是在實際的計算中只考慮沿導彈軸向的作用載荷，而忽略其他方向的力及力矩。

1.3 發射箱結構有限元分析

在對發射箱進行結構優化設計之前必須對其進行結構有限元分析，以便確定優化的目標和方向。

某型導彈發射箱的靜力學分析是運用ANSYS 程序完成的，其求解過程如下:

1)進入/PREP7 前處理器進行前處理

a.設置分析環境，定義工作文件名和工作標題;

b.定義單元類型

發射箱的箱體采用板單元SHELL181 來劃分，加強筋采用BEAM188 單元來劃分;

c.定義材料類型

發射箱的材料采用的是鋁鎂合金，取其彈性模量為7 ×104MPa，泊松比為0.3，密度為2.7 ×103kg/m3;

d.建立發射箱幾何模型，劃分網格。

按照實際結構尺寸，運用自底向上的方法建立發射箱幾何模型。先從關鍵點開始建立，然后再建立更高級的元素，依次為線和面。幾何模型建立以后劃分網格，完成發射箱有限元模型的建立，如圖2 所示。其中一共劃分節點13 400個，單元13 366個，其中板單元11 398個，梁單元1 968個。

圖2 發射箱有限元模型

2)進入/SOLU 求解器加載求解

a.施加約束及作用力;

b.設置分析類型為靜力學(Static)，進行求解;

c.設置分析類型為模態分析(Modal)，模態提取方法為Block Lanczos 法，進行求解。

3)后處理

進入通用后處理器/POST1，查看發射箱節點總位移和Von Mises 應力分布，如圖3 和圖4 所示。

從圖中可以看出發射箱最大總位移為1.347 mm，這是非常小的，而最大Von Mises 應力僅為13.3 MPa，遠小于發射箱鋁鎂合金材料的屈服極限(77 ～125 MPa)，而且發射箱結構大部分區域的變形和應力還遠小于這兩個值，所以該發射箱存在優化減重的余地，有必要對其進行優化設計分析。

圖3 發射箱總位移分布

圖4 發射箱Von Mises 應力分布

在通用后處理器中查看發射箱一階模態頻率為23.92 Hz。一般以第一階模態的固有頻率作為衡量結構穩定性的依據，所以在對發射箱進行結構優化時也必須要考慮到這一點。

2 發射箱結構優化設計分析

2.1 發射箱結構優化數學模型

1)設計變量

選取設計變量時應注意的問題如下:

a.設計變量變化范圍選取的優劣很大程度上依賴于對研究對象的熟悉程度。要給設計變量定義一個合理的范圍，范圍過大可能不能表示好的設計空間，而范圍過小可能排除了好的設計;

b.定義盡量少的設計變量。選用太多的設計變量會使得優化收斂于局部最小值的可能性增加，也需要更多的迭代次數，從而需要更多的機時;

c.選擇可以提供實際優化效果的設計變量，要避免產生不切實際的結果或者是不符合需要的設計方案。

前文已經對發射箱進行了結構分析和簡化處理，可知簡化的發射箱結構由橫截面為長方形的薄壁箱體和截面為帽形的環形加強筋兩部分組成。很顯然，對發射箱質量具有影響的結構參數即是箱體和加強筋的尺寸，于是選取發射箱的壁厚T 和加強筋的厚度TH 及其截面的形狀參數W、W1和W2等5 個參數(如圖5 所示)作為設計變量。這里考慮到加工工藝性，取箱壁和加強筋的厚度在各個位置都是一樣的，并且使加強筋截面2 個“帽沿”的寬度保持一致，均為W1。

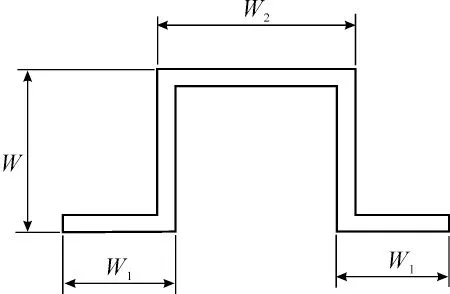
圖5 加強筋截面形狀參數

2)狀態變量

狀態變量也即優化約束變量，本文選擇發射箱最大總位移Umax、最大Von Mises 等效應力Smax和一階固有頻率FREQ1 作為狀態變量。

參照前文對發射箱的靜力學分析和模態分析的結果，可暫確定各狀態變量的約束范圍:Umax≤2 mm;Smax≤30 MPa;FREQ1 ≥20 Hz。

3)優化目標

優化目標是實現發射箱質量最輕，由于發射箱結構各處的材料是相同的，所以可選擇實現發射箱的體積V 最小作為優化目標。發射箱的體積為

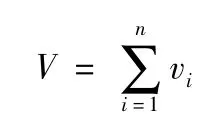
其中:vi為第i 個單元的體積;n 為單元總數目。

于是可確定發射箱結構優化的數學模型如下:

目標函數:

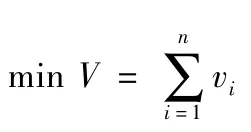
位移約束:

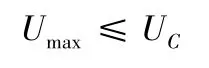
應力約束:

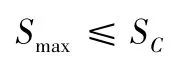
頻率約束:

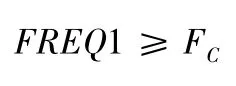
設計變量:

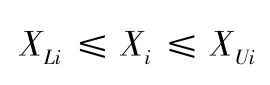
其中:UC是允許的最大變形量，取值為2 mm;SC是允許的最大應力，取值為30 MPa;FC是允許的最小一階頻率，取值為20 Hz;Xi是設計變量，XLi和XUi分別是設計變量下限和設計變量上限。

2.2 ANSYS 優化模塊

本文運用ANSYS 軟件對結構優化設計，所以有必要對ANSYS 優化模塊進行簡單的介紹，以確定對發射箱進行結構優化設計分析的方法和步驟。

ANSYS 優化模塊(Optimization Module)是ANSYS 程序的重要組成部分之一，可用來確定優化設計方案，在某些特定的約束條件下還能尋求最優化的設計方案。ANSYS 優化程序的設計變量、狀態變量以及目標函數是通過ANSYS 參數化設計語言(APDL)中的標量參數來定義的，所以APDL的編制在ANSYS 優化進程中是必須的步驟。ANSYS 優化模塊主要提供了2 種優化方法:

1)零階方法

零階方法是ANSYS 提供的一種通用的函數逼近優化方法，本質是采用最小二乘逼進，求取一個函數面來擬和解空間，然后對該函數面求極值。這是一種普遍適用的優化方法，不易陷入局部極值點。

2)一階方法

一階方法是對零階方法的改進，是一種局部尋優方法，也叫梯度尋優。

一般來說，一個比較完善的優化問題需要同時采用兩種優化方法，先用函數逼近的零階方法初步求得最優解基本位置，然后再用梯度尋優的一階方法對最優解的位置進行更精確的確定［3］。

2.3 發射箱結構參數優化設計

參照發射箱結構優化數學模型，運用ANSYS 優化模塊，即可進行發射箱的結構優化設計計算。

1)構建發射箱結構優化分析文件

a.運用APDL 建立發射箱的參數化有限元模型;

b.加載進行靜力學求解，獲取優化變量:發射箱體積VOLUME 和最大變形量Umax、最大應力Smax;

c.進行模態求解，獲取優化變量:一階振型固有頻率FREQ1。

將以上步驟的APDL 程序保存成TXT 格式，命名為OPTIMIZATION，此即為本文對發射箱進行結構優化的優化分析文件。

2)進入優化設計器/OPT，采用零階方法執行發射箱結構優化設計

a.指定優化分析文件為前面步驟建立的OPTIMIZATION.TXT;

b.定義優化變量;

c.指定優化方法，進行優化求解

選擇優化方法為零階方法(SUBP)，優化選項采用默認值，即最大循環次數為30，不可行解最大連續出現次數為7次。運行OPEXE 命令，進行優化循環求解;

d.查看優化設計序列

運行* STATUS 命令，查看發射箱結構優化的最優設計序列。求解結果顯示，最優優化序列為第28 列，該序列結果與初始值對比如表1 所示。

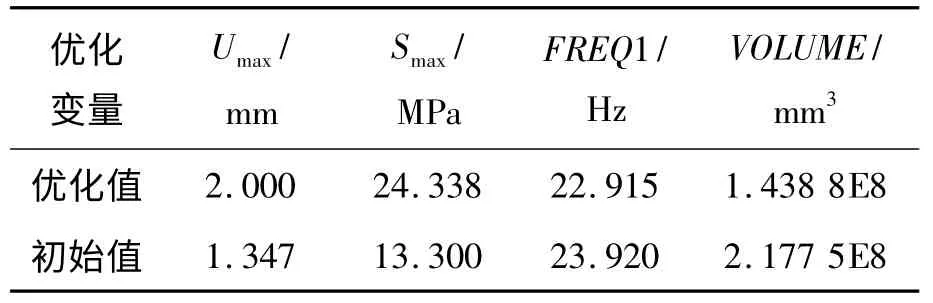
表1 優化結果與初始值對比

優化后的發射箱體積比初始值減少了33.9%，優化減重效果可以說是非常的明顯。該優化序列對應的設計變量如表2 所示。

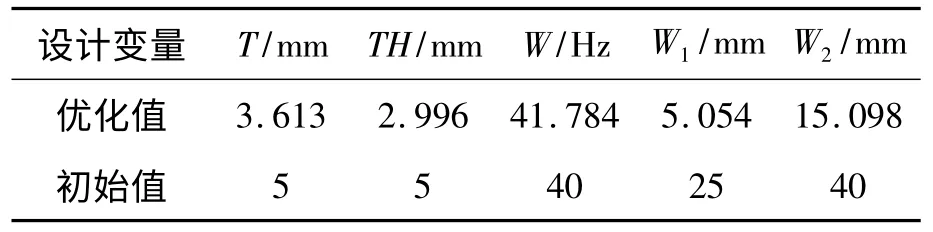
表2 優化前后設計變量對比

從表2 中我們可以看出，在這一優化設計序列中，發射箱最大變形為2 mm，比初始值增加幅度較大，而最大等效應力雖然仍遠小于材料的屈服極限，但與初始值相比，增幅也是不小的。

3)采用一階方法進行發射箱結構優化

如前所述，第一次結構優化的減重效果固然明顯，但是導致發射箱的最大變形量和最大等效應力比初始值增加較多，這主要是由于采用零階方法執行優化時，為確保能夠尋找到最優的設計序列，將約束變量Umax和Smax的上限設置的過大，下面嘗試減小這2 個變量的上限，并采用一階方法進行第二次優化設計。

運行OPLIST，ALL 命令，顯示前次優化的全部30 個設計序列，并從中找出約束變量Umax和Smax與原始值相差不大的可行設計序列。經過對比分析，選擇到第4 個序列，如表3所示。

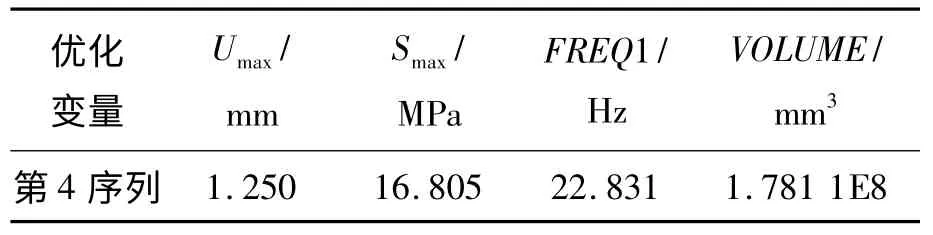
表3 第4 序列優化結果

第4 優化序列對應的設計變量值如表4 所示。

表4 第4 序列設計變量

參照這一設計序列將最大變形量Umax和最大等效Von Mises 應力Smax的上限分別改為1.5 mm 和16.8 MPa，一階頻率的上限也改為25，并將設計變量的初始值改為第4 個序列所對應的值。此外，優化方法也更改為一階方法(FIRST)，優化迭代次數設置為50，運行OPEXE 命令，執行第二次優化。經過求解運算得到了優化結果，如表5 所示。

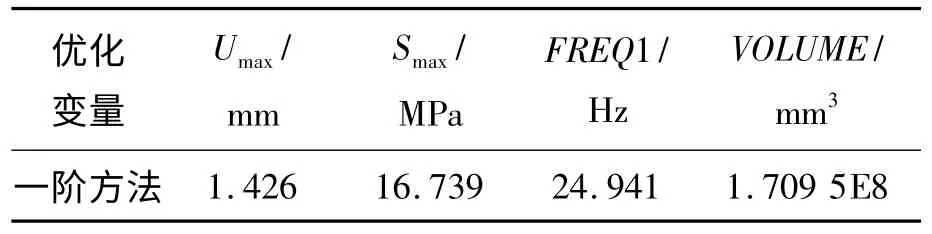
表5 一階方法優化結果

對應的設計變量值如表6 所示。實際確定結構尺寸時，要對得到的設計變量進行圓整，圓整后的結果即是最終的優化設計方案，與初始值的對比如表6 所示。

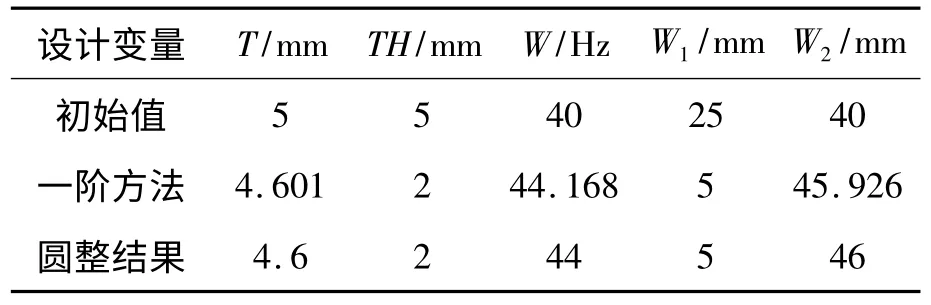
表6 最終優化方案與初始值對比

從表中可以看出，在最終的優化方案中，發射箱的壁厚T 略微變薄了0.4 mm;加強筋的厚度TH 由5 mm 減小為2 mm，減幅較大;加強筋高度W 比原來增加了4 mm;其帽形截面中間部分的寬度W2增至46 mm，而邊緣的寬度W1從25 mm減到了5 mm，減幅最大。

按照最終確定的設計方案，重新建立發射箱有限元模型并加載求解，最終結果如表7 所示。

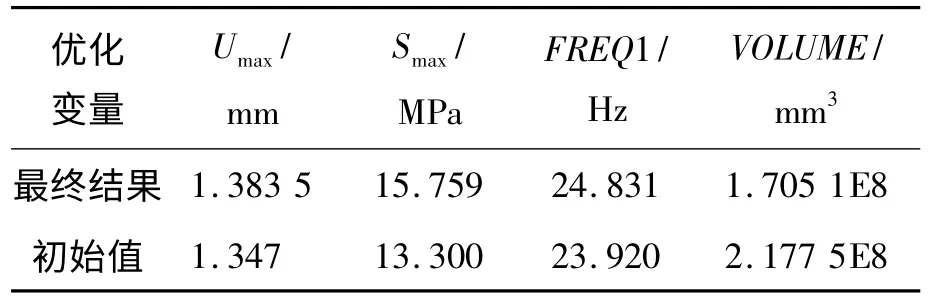
表7 最終優化結果與初始值對比

最終的優化結果與初始值相比，在幾乎沒有改變發射箱結構性能的情況下，卻使其質量減輕了21.7%，優化效果非常顯著。

3 結束語

本文基于結構優化理論和方法，運用ANSYS 優化模塊對發射箱進行結構優化設計分析，在發射箱變形和應力與原來結構相比改變很小、一階振動模態甚至有所提高的前提下，成功的使發射箱的質量減小了1/5 還多，減重效果顯著，優化結果令人滿意，充分說明了該方法是可行的。

［1］胡黎明，高凱.飛航導彈輕型發射箱結構優化技術研究［J］.戰術導彈技術，2008 (4):12-14.

［2］姚昌仁，唐國梁.火箭導彈發射裝置設計［M］.北京:北京理工大學出版社，1998:209-217.

［3］博弈創作室.APDL 參數化有限元分析技術及其應用實例［M］.北京:中國水利水電出版社，2004:1-11.

［4］韓志強.某發射裝置上架的減重技術研究［D］.南京:南京理工大學，2006.

［5］王明真.輕型火炮大架的優化設計［D］.南京:南京理工大學，2005.