助推－滑翔導彈再入彈道快速優化①

趙 欣，閆循良，張金生，王仕成，何安榮

(1.第二炮兵工程大學，西安 710025;2.第二炮兵駐211廠軍代室，北京 100084)

助推－滑翔導彈再入彈道快速優化①

趙 欣1，閆循良1，張金生1，王仕成1，何安榮2

(1.第二炮兵工程大學，西安 710025;2.第二炮兵駐211廠軍代室，北京 100084)

基于LGL(Legendre-Gauss-Lobatto)偽譜法，研究了臨近空間助推-滑翔導彈再入段彈道快速優化問題。首先，基于改進的氣動力模型建立了較為精確的再入數學模型;其次，針對該優化問題在氣動數據處理和優化求解上存在的困難，基于LGL偽譜法系統地建立了再入最優飛行彈道的求解步驟，為解決直接利用LGL偽譜法存在的困難，設計了一種基于LGL偽譜法的串行優化求解策略;最后，分別采用積分推進法和協狀態映射原理對優化結果進行了可行性和最優性驗證。仿真結果表明，本文的彈道優化方法優化1條再入彈道所用時間為3～4 s，計算效率較高，路徑約束和端點約束均得到很好滿足，算法求解精度較高，有效地實現了多約束多變量大型稀疏的再入彈道導彈快速優化。

臨近空間;助推-滑翔導彈;再入彈道優化;偽譜方法;優化控制

0 引言

當前，由于導彈防御系統彈道預測性不斷增強，彈道導彈所面臨的生存環境越來越惡劣。近些年，為提高導彈的戰場生存能力，各軍事強國競相關注并研究中段突防變軌技術［1］，而助推-滑翔導彈正是在這一技術發展中應運而生的新概念武器［2］。助推-滑翔導彈采用升力體形，依靠氣動力控制，可在臨近空間區域長時間高超聲速滑翔飛行，從而實現遠程快速攻擊，其地位具有深遠戰略意義。

在臨近空間助推-滑翔導彈的研究中，再入彈道優化是系統總體優化中的關鍵技術之一，它直接影響武器的整體突防性能。然而，由于這類導彈的再入彈道對控制變量高度敏感，且再入過程的非線性約束較強，致使彈道的可行域范圍較窄，這決定其再入彈道數值優化存在一定困難［3］。目前，求解彈道優化問題的主流方法有:基于極大值原理的間接法和基于非線性規劃理論的直接法［4］。間接法將最優控制問題最終轉換為一個兩點邊值問題［5］，可以獲得精確的最優解，但其要求求解狀態方程和協態方程，這對于復雜的非線性動力學方程來說較為麻煩，計算量較大;同時，求解過程對共軛變量的初值高度敏感且難以估計，很難收斂，且算法魯棒性較差。直接法采用參數化方法將連續空間的最優控制問題求解轉化為一個非線性規劃(Non Linear Programming，NLP)問題，通過數值求解非線性規劃問題來獲得最優軌跡。與間接法相比，直接法具有以下優點:(1)算法簡單、易于理解;(2)對初始值要求不嚴格，收斂半徑大，魯棒性好;(3)易于處理包含路徑約束的最優控制問題［6］。因此，直接法在解決實際問題的適應性上更具有優勢。

直接法又可分為2種基本類型:一是離散控制變量(又稱直接打靶法)［7］;二是同時離散控制變量和狀態變量(又稱直接配點法)［8］。前一種方法的主要不足點是節點數目不易確定，取得過少會導致所得到的最優控制解不準確，過多則會增大非線性規劃問題的規模，出現“維數災難”;后一種方法中，一般的直接配點法由于采用分段多項式來近似狀態和控制變量時間歷程，使得設計變量數目龐大，且初值不易給定，控制曲線不光滑。

近些年發展起來的偽譜法(PSM)開始應用于軌跡優化問題，它也是配點法的一種，它采用全局插值多項式有限基在一系列離散點上近似狀態變量和控制變量，相對于一般的配點法，PSM能以較少的節點獲得較高的精度［9-10］。同時，采用PSM轉化得到的NLP問題的KKT(Karush-Kuhn-Tucker)條件與原最優控制問題一階最優必要條件的離散形式具有一致性［11］，彌補了一般直接法的不足。上述特點使得PSM成為目前求解復雜最優控制問題最為有效的方法之一。

本文研究Legendre-Gauss-Lobatto(LGL)PSM在臨近空間助推-滑翔導彈再入彈道優化中的應用。首先，從工程應用角度出發建立了與真實飛行環境比較相符的臨近空間助推-滑翔導彈以再入時間最短為目標的多約束彈道優化模型;在此基礎上，采用基于LGL PSM和序列二次規劃(SQP)算法的串行優化求解策略處理問題;最后，采用解析法對優化結果進行了可行性和最優性驗證。通過仿真對上述方法進行了數值驗證。

1 再入彈道優化問題數學模型

所研究問題的數學模型包括再入動力學模型、氣動力模型和大氣模型。

1.1 再入動力學模型

基于相關假設，考慮地球自轉效應，升力式再入飛行器三自由度無量綱動力學方程為

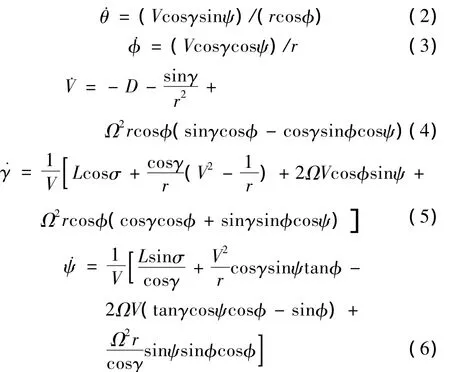
式中r為再入飛行器質心到地球球心的無量綱地心距;θ和φ分別為再入飛行器質心位置的經度和緯度;V為相對地球的無量綱速度;γ為彈道傾角;ψ為速度方位角;Ω為無量綱地球旋轉角速度;σ為傾側角;D和L分別為無量綱的阻力加速度和升力加速度。

1.2 改進的氣動力模型

目前，再入軌跡優化中的氣動力模型一般采用傳統簡化形式，即只將氣動系數視為攻角函數［3］。然而，實際上氣動系數受多種因素的影響，其中攻角α和飛行速度Vm是主要的2個因素，為進一步減小因模型不精確引入的誤差，需給出更為精確的氣動力模型。文獻［12］研究指出，升力系數與攻角近似呈線性關系，與馬赫數近似呈負指數變化關系;阻力系數與攻角近似呈二次函數關系，與馬赫數也近似呈負指數變化關系。基于此，給出如下的改進的氣動力系數模型:

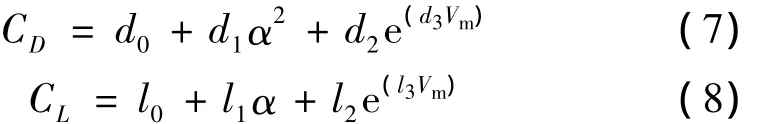
其中，d0、d1、d2、d3、l0、l1、l2、l3均為模型的待辨識參數，本文采用非線性最小二乘法進行辨識。

1.3 大氣模型

大氣密度模型一般采用1976標準大氣模型，該模型為一分段函數，給出了大氣密度和聲速隨高度變化的函數。具體模型見文獻［13］。

2 再入彈道優化模型

2.1 再入狀態變量和控制變量選擇

再入優化問題狀態變量為

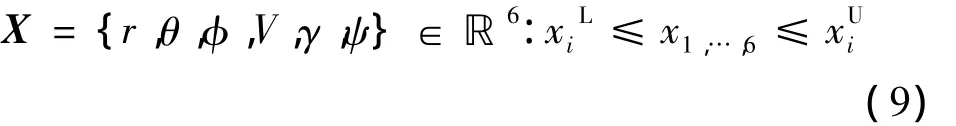
不考慮指令延遲，控制變量可以選擇為攻角α和傾側角σ，因此得到控制空間為

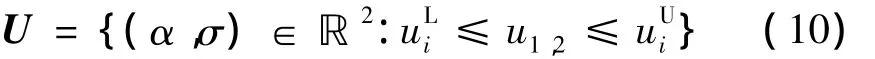
根據以上分析，得到優化變量為(r，θ，φ，V，γ，ψ，α，σ)共8個參數。若設計攻角剖面為馬赫數的分段線性函數，則優化控制量只有σ。因此，新的優化變量為(r，θ，φ，V，γ，ψ，σ)，共 7 個參數。

2.2 再入彈道約束

再入飛行過程是一個高動態的過程，需滿足一系列苛刻約束條件的限制，如過載限制、動壓限制、熱流限制和初終端條件限制等。

(1)熱流約束

再入熱流約束一般是指對飛行器表面駐點處的熱流限制，其數學表達式為

駐點熱流計算式為

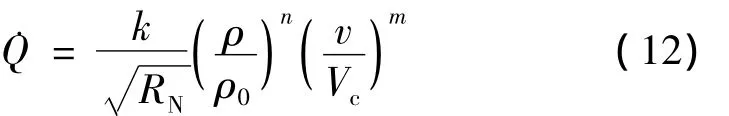
式中 ρ分別為無量綱大氣密度;RN為駐點曲率半徑;k、ρ0、Vc為常數;v為飛行速度;n由邊界層的特性決定，一般情況下把駐點附近的邊界層按照層流處理，此時n=1/2;m則需根據氣體的粘性等因素來確定，本文取3.25;再入飛行熱流限制取=7 000 kW/m2。

(2)過載約束

最大總過載限制主要取決于再入飛行器結構強度和機載設備的可承受過載范圍。再入飛行器總過載表達式滿足:

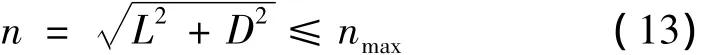
式中nmax為額定最大值，文中取20gn。

(3)動壓約束

再入飛行過程中的動壓約束一方面取決于隨動壓增大而增大的氣動控制鉸鏈力矩;另一方面取決于飛行器表面防熱材料的強度。動壓約束為

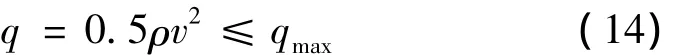
其中qmax為最大動壓，文中取qmax=3×105N/m2。

(4)端點條件

再入點初始時刻需滿足一定的條件，同時考慮到與末制導段交班的要求，再入終端狀態也應滿足一定的條件，端點約束條件為

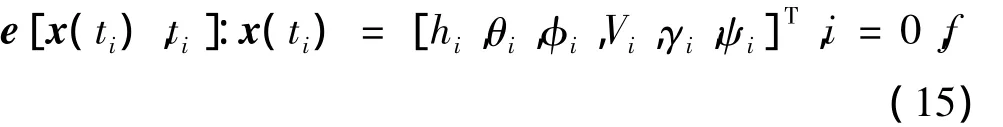
2.3 優化目標函數

對于導彈武器系統而言，再入點和目標點確定后，飛行時間是一個重要指標，即要在盡量短的時間內攻擊目標，提高武器的快速打擊性能。所以，選取到達目標點飛行時間最短作優化性能指標:

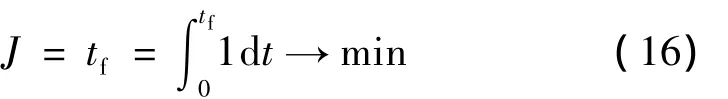
3 基于LGL偽譜法的再入段彈道優化問題求解

3.1 彈道優化問題描述

上述再入彈道優化問題可歸納為以Bolza型為優化目標的非線性最優控制問題:

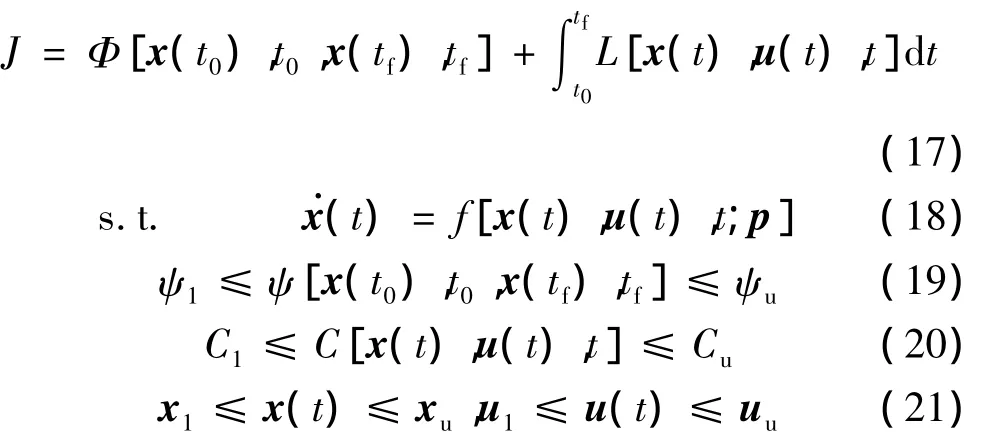
式(17)～式(21)分別對應彈道優化問題的目標函數、動力學方程、邊界條件、路徑約束、狀態量和控制量自身范圍約束。

3.2 基于LGL偽譜法彈道優化問題的轉化

(1)區間變換處理

軌跡優化問題的時間區間為［t0，tf］，而LGL偽譜法通過τ∈［-1，1］上的拉格朗日多項式擬合控制量和狀態量。因此，需將時間區間轉換至［-1，1］，最終得到上述最優控制問題的新形式為

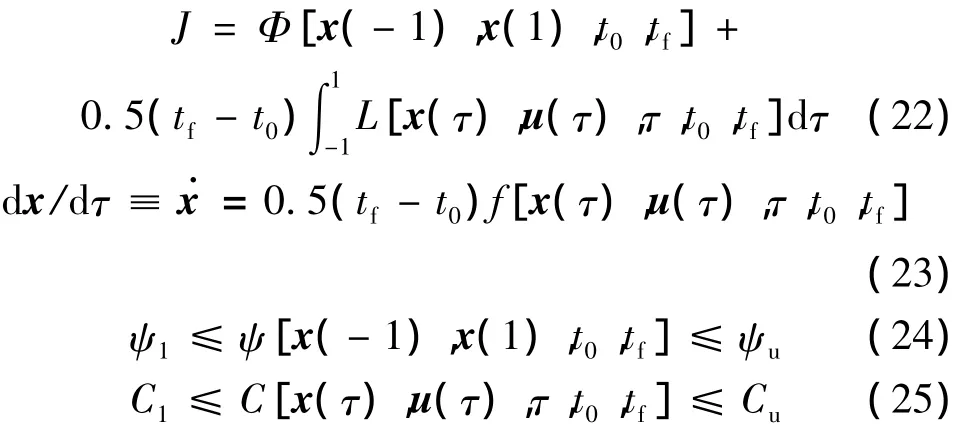
(2)時間區間劃分及LGL點

設將時間歷程劃分為N個子區間，則有N+1個LGL 點 τi(i=0，1，…，N)，其中 τ0=-1，τN= τf=1;中間節點 τi(i=1，2，…，N-1)為N階 Legendre多項式的導數˙LN的零點。其中，LN為N階Legendre正交多項式。這些點在［-1，1］上并不是均勻分布的，而是兩端密集，中間稀疏，有利于提高擬合精度。

(3)控制變量和狀態變量近似

對狀態變量和控制變量基于LGL點進行拉格朗日插值近似

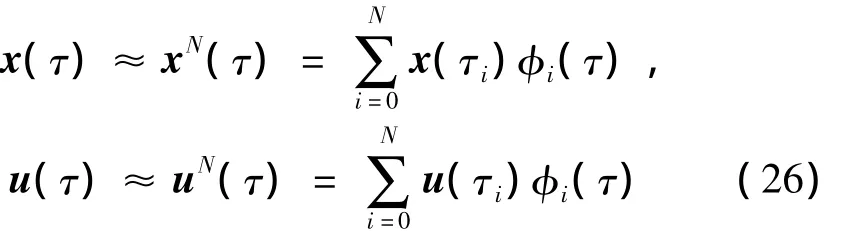
式中 φi(·)為N階拉格朗日多項式。

在LGL點可得到以下關系式:

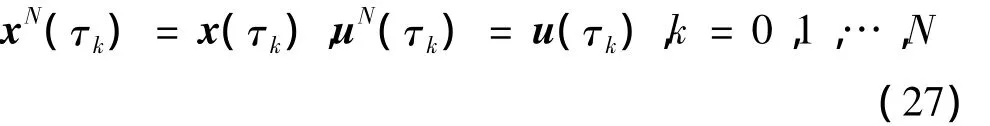
(4)動力學微分方程約束處理

對連續微分約束用插值多項式的微分來代替，對狀態近似方程進行微分，在LGL點進行擬合得:

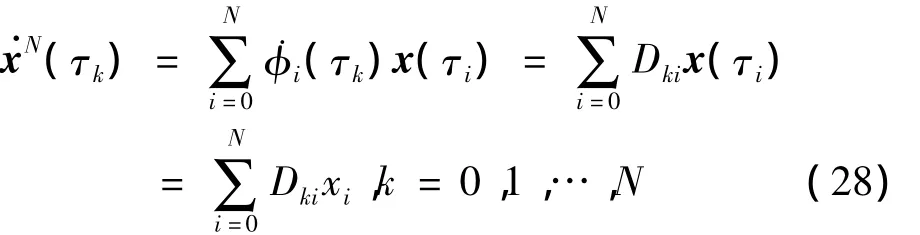
式中Dki為(N+1)×(N+1)階微分矩陣D的元素。

動力學微分方程約束可近似轉換為代數約束，在LGL點擬合得到:

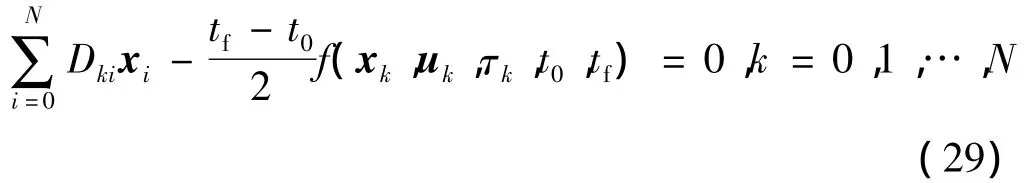
(5)性能指標近似

采用Gauss-Lobatto積分準則對性能指標中的積分項進行數值積分，得到離散的性能指標函數:

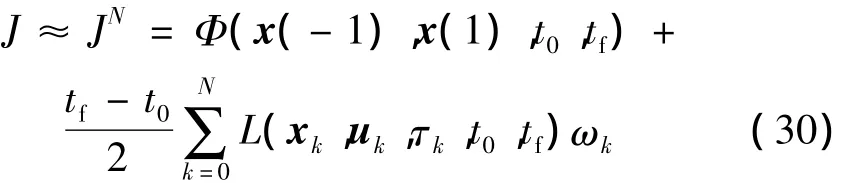
其中，LGL權:

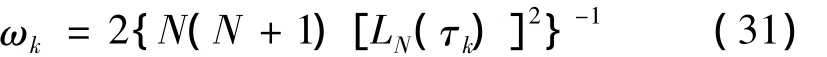
通過以上對最優控制問題在LGL點近似，得到了以下離散化的非線性規劃問題，即尋找最優參數X=(x0，x1，…，xN)，U=(u0，u1，…，uN)，t0，tf，使得性能指標JN(X，U)最小化，同時滿足代數方程約束、端點約束、路徑等約束。其中，優化變量數目為(n+m)(N+1)+2，約束數目為(n+c+m)(N+1)+q。可見，上述離散得到的問題為一大型稀疏NLP問題，對于這類問題的求解，本文采用序列二次規劃(SQP)算法，它被認為是目前求NLP問題最有效的方法之一［14］。

3.3 基于LGL偽譜法的串行快速優化策略

理論上，上述LGL偽譜法可直接求解本文研究的問題，然而實際應用中存在以下因難:再入軌跡優化由于狀態量和控制量數目較多，如果選取節點數目較多時，優化設計變量的數目將會十分龐大，同時得到的約束方程數目也是非常巨大的，這會大大增加計算負擔。另外，對于大范圍再入問題，設計變量的初始猜測較為復雜，不恰當的初值會帶來計算代價的增加，甚至可能導致問題不收斂或收斂到不可行解。針對再入彈道優化存在的問題，為了提高算法的計算速度及收斂性，本文采用基于LGL偽譜法的串行快速優化策略來進行最優彈道的求解。

(1)設計初值生成器

利用LGL偽譜法能以較少節點獲得高精度的優勢，先采用較少的節點，計算最優軌跡和最優控制，并以此為下一步精確計算的初值。

(2)采用從可行解到最優解的串行優化策略

串行優化策略是指，不直接找尋滿足所有等式約束和不等式約束的解，而是先將等式約束轉換為目標函數，將得到的最優解x0作為初值，求解原非線性問題的解。

具體流程:首先，基于從可行解到最優解的策略，由初值生成器獲得初值;再選取較多的節點，以求得高精度的最優軌跡和最優控制。

3.4 可行性和最優性驗證

為了證明極值解的合理性，研究中進一步完成了優化解的可行性和最優性驗證工作。

(1)基于積分推進法的可行性驗證

采用積分推進法進行極值解的可行性驗證，具體方法:在保證所有約束滿足的前提下，利用所得到的控制量，積分推進運動方程得到狀態量軌跡，通過比較優化獲得的狀態量和積分推進得到的狀態量軌跡，進行解的可行性驗證。如果二者匹配程度在可接受的誤差范圍內，證明解是可行的。

(2)最優性驗證

采用Covector Mapping Principle(CMP)進行一階最優性驗證，即根據龐特里亞金極小值原理，增廣哈米爾頓函數 ˉH滿足 ?ˉH/?u=0，將其重新改寫，得到控制律的顯示表達，將解析得到的控制量與優化得到的控制量進行比較，如果二者是一致的，則一階最優性是滿足的;同時，根據KKT定理可得到相應的補充條件，判斷補充條件是否成立，最終實現結果的最優性驗證。

4 仿真算例

4.1 再入仿真條件

再入端點條件為

其中，考慮上述初值設定，對應的狀態邊界條件為

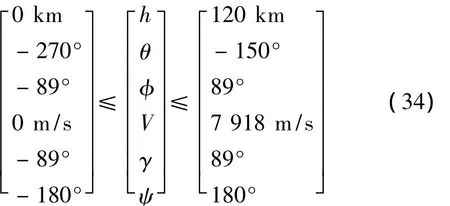
對應的各控制量邊界為

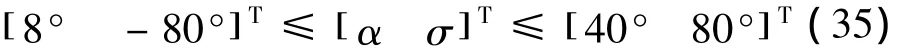
路徑約束已經在前文中給出。若設計攻角剖面為馬赫數的分段線性函數，即

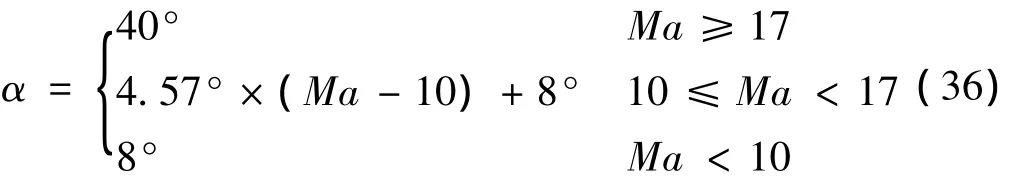
則優化控制量只有σ，因此新的優化變量為(r，θ，φ，γ，ψ，σ)，共7 個參數。

4.2 仿真結果及分析

采用初值生成技術和從可行解到最優解的串行優化技術進行求解。初值生成器中取LGL節點數目為5，則離散化之后得到最終優化變量數目為36，綜合考慮各種約束的總約束數目為60。將優化結果作為初值進行多節點優化，選取多節點數目為30，則最終優化變量數目為211，總約束數目為310。

優化需要的目標函數及約束的梯度函數(即雅可比陣)采用解析方法提供。最終，優化指標達到全局最小值為972.93 s，狀態量及控制量優化結果如圖1～圖3所示，各路徑約束的約束變量曲線如圖4所示。

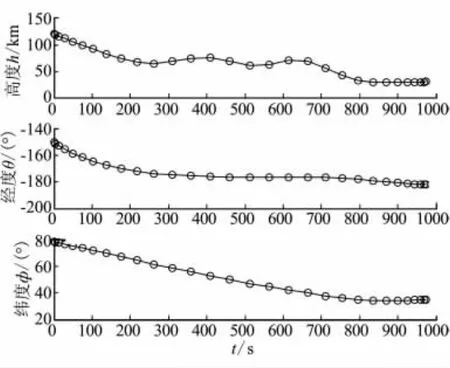
圖1 位置變化曲線Fig.1 Curves of position vs time

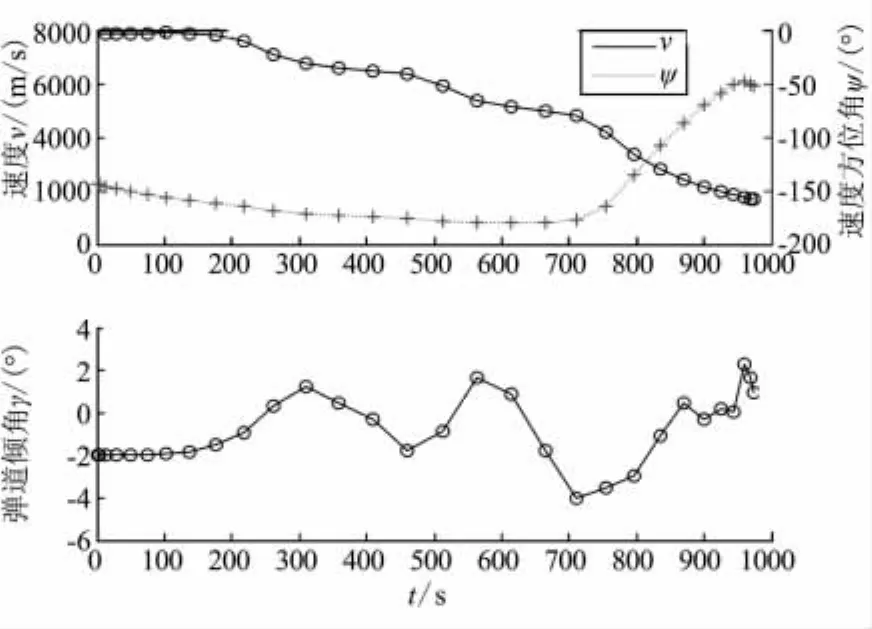
圖2 速度相關狀態量變化曲線Fig.2 Curves of state variables correlated with velocity vs time

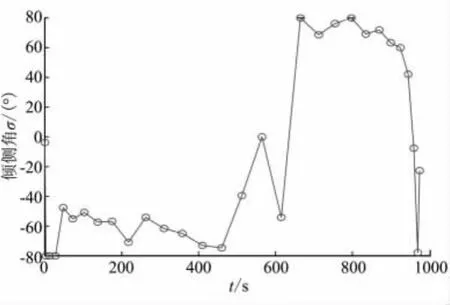
圖3 最優控制傾側角變化曲線Fig.3 Curves of optimal bank angle vs time

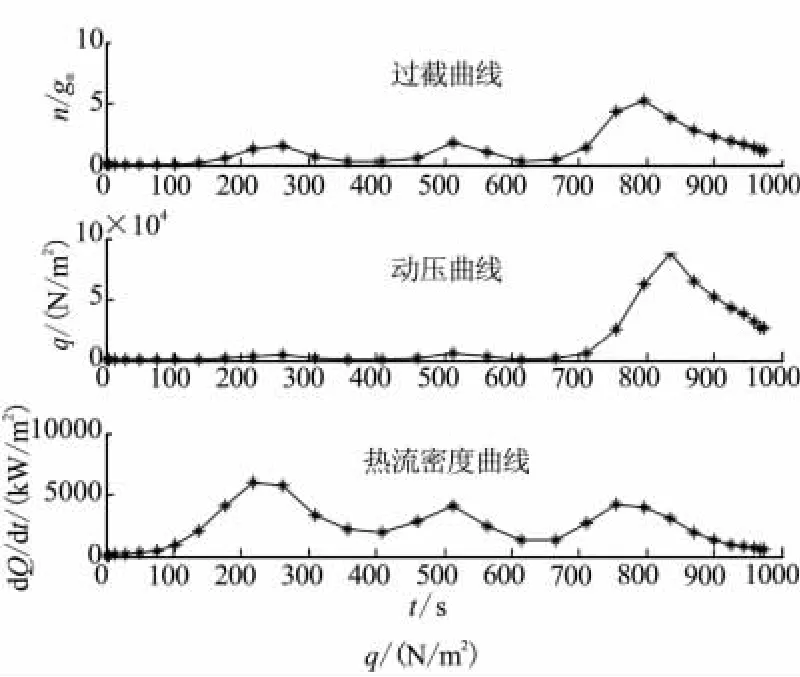
圖4 內點路徑約束曲線Fig.4 Curves of interior point constraints

優化計算在CPU為E7500/2.93 GHz，2G內存的臺式計算機上實現，操作系統為Windows XP。采用MATLAB7.7.0(R2008b)語言進行代碼編寫，MATLAB環境下進行仿真，SQP算法實現參數優化計算。算例中再入彈道優化的時間包括初值生成時間和精確計算時間兩部分，總耗時為3.72 s;直接采用3.2節中的LGL偽譜法，優化計算初值根據再入初始條件和終端條件線性插值簡單給出，LGL點個數取30，優化計算所需時間為58.64 s，說明設計的快速優化策略大大提高了優化計算速度。另外，相對于傳統優化算法，由于LGL偽譜法不包含積分計算，且離散得到的NLP問題具有典型的稀疏結構。所以，從這兩點也可說明這種方法具有較高的計算效率。

另外，相關文獻研究指出，若在LINUX環境下，采用C或Fortran語言編寫代碼，并將代碼進一步優化，可使得計算速度提高至少100倍［15］。可見，在計算速度上，利用LGL偽譜法求解助推-滑翔導彈再入彈道優化問題，計算效率較高。

由圖1～圖4的仿真結果可看出，所得結果滿足所有端點約束條件，同時滿足各種路徑約束，本文建立的優化方法能以較少的節點和計算時間獲得狀態量的優化解和優化的控制量。

進一步進行可行性驗證。將得到的最優控制量σ*(t)進行插值，得到整個時間區間上的σinterp1(t)，采用MATLAB的ode45龍哥庫塔積分器，積分推進運動方程可得到狀態量推進軌跡，將此結果與本文得到的優化狀態量進行對比，得到圖5～圖7所示結果。

由圖5～圖7的對比結果可看出，優化結果與推進結果吻合較好，雖然也存在一定的誤差，但對于本文所研究的大范圍的變軌問題而言，其相對誤差(定義為絕對誤差/變量值)是較小的，數量級在10-4～10-5左右，說明計算精度較高。即在理想的飛行條件下，臨近空間助推-滑翔導彈按照LGL偽譜法獲得的最優制導指令進行飛行，可從預定初始點到目標點并實現交接班，從而驗證了極值解的可行性。

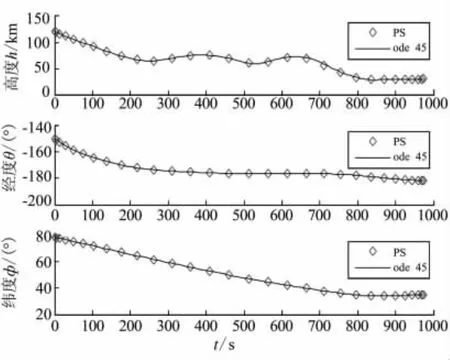
圖5 位置比較Fig.5 Comparison of positions

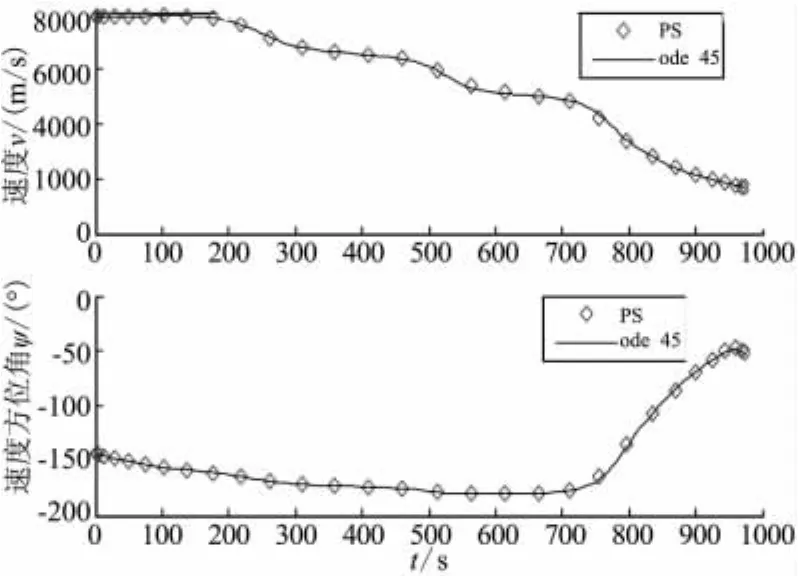
圖6 速度及速度方位角比較Fig.6 Comparison of velocity and velocity azimuth

進一步分析偏差存在的原因主要有:

(1)偽譜法離散所選取的LGL節點數目為30，這個點的數目是較少的，要進一步提高精度，必須增加節點數;

(2)由于本文選擇傾側角而不是傾側角速率作為控制量，這導致無法對傾側角變化率進行限制，致使傾側角的變化較為劇烈，而本文采用樣條曲線對控制量進行擬合(見圖8)，插值所得控制量并不能與優化結果很好地吻合，致使狀態量推進結果并不能完全真正地反映最優控制量的作用。

接下來進行最優性驗證。本文利用解析法驗證問題的一階最優性，驗證原則:Hamiltonian函數沿最優軌線保持為零。采用CMP對協狀態進行估計，最終得到該問題的Hamiltonian，如圖9所示。可見，通過CMP及解析驗證法得到的Hamiltonian在零附近震蕩，滿足一階最優性必要條件。

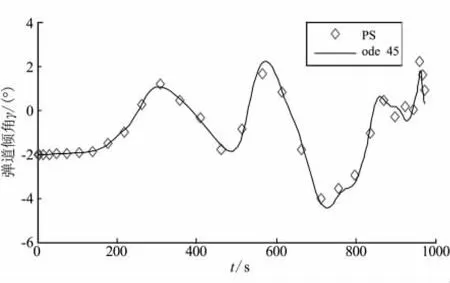
圖7 彈道傾角比較Fig.7 Comparison of trajectory obliquity

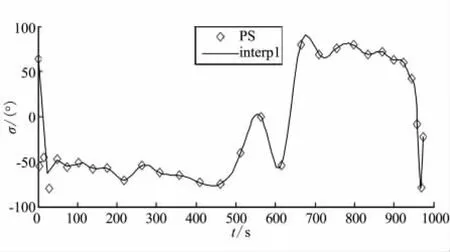
圖8 控制量優化結果與插值結果的比較Fig.8 Comparison of optimal result and interpolation result of the controller

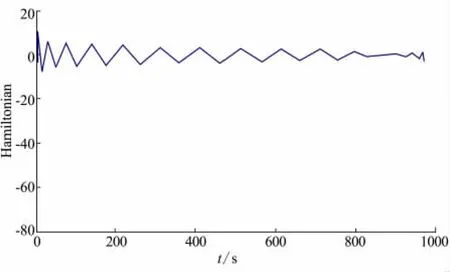
圖9 最優控制的HamiltonianFig.9 Hamiltonian of optimal control

同時，給出控制量傾側角對應的拉格朗日乘子變化曲線，如圖10所示。可知，乘子μσ滿足KKT定理。因此，極值解的最優性得到了驗證。

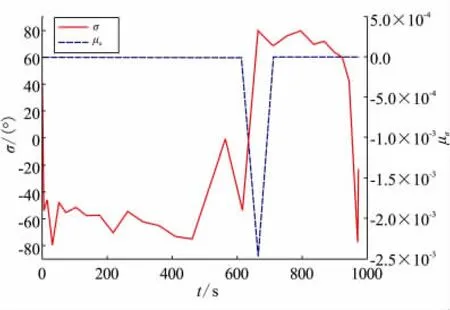
圖10 傾側角與對應的KKT乘子曲線Fig.10 Curves of bank angle and KKT multiplier

5 結論

(1)針對臨近空間助推-滑翔導彈再入彈道快速優化問題，建立了多參數、多約束的再入彈道優化模型。

(2)利用LGL偽譜法和SQP相結合的方法詳細建立了再入最優飛行彈道的求解步驟，針對直接利用該方法的困難，設計了含初值生成器串行優化求解策略，有效解決了助推-滑翔導彈再入段彈道快速優化問題。仿真結果表明，對于再入彈道的優化求解，LGL偽譜法具有較高的計算效率和計算精度，能夠實現多約束、多變量、大型稀疏的再入軌跡快速優化。

(3)完成了極值解的有效性檢驗，計算分析表明，優化結果滿足極小值原理對應的最優性必要條件。

(4)本文的研究成果能提供實時或近實時、開環最優解，可為在線制導、反饋控制的設計提供基本保證。

［1］徐瑋，孫丕忠，夏智勛.助推-滑翔導彈總體一體化優化設計［J］.固體火箭技術，2008，31(4):317-320.

［2］李瑜，楊志紅，崔乃剛.洲際助推-滑翔導彈全程突防彈道優化［J］.固體火箭技術，2010，33(2):125-130.

［3］陳小慶，侯中喜，劉建霞.高超聲速滑翔式飛行器再入軌跡多目標多約束優化［J］.國防科技大學學報，2009，31(6):77-83.

［4］Betts J T.Survey of numerical methods for trajectory optimization［J］.Journal of Guidance，Control，and Dynamics，1998，21(2):193-207.

［5］Gergaud J，Haberkorn T.Orbital transfer:some links between the low thrust and the impulse cases［J］.Acta Astronautica，2007，60:649-657.

［6］Hui T L，Ping Y J，Qun F，et al.Reentry skipping trajectory optimization usingdirectparameteroptimization method［C］//14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference，2006.

［7］Gao Y，Li W Q.Systematic direct approach for optimizing continuous-thrust earth-orbit transfers［J］.Journal of Aeronautics，2009，22:56-69.

［8］Desai P N，Conway B A.Six-degree-of-freedom trajectory optimization using a two-timescale collocation architecture［J］.Journal of Guidance，Control，and Dynamics，2008，31(5):1308-1315.

［9］Geoffrey T Huntington，David Benson，Anil V Rao.A comparison of accuracy and computational efficiency of three pseudospectral methods［R］.AIAA 2007-6405.

［10］Bemon A，Thorvaldsen T，Rao V.Direct tmjectory optimization and costae estimation via an orthogonal collocation method［J］.Journal of Guidance，Control，and Dynamics，2006，29(6):1435-1440.

［11］楊希祥，張為華.基于Gauss偽譜法的固體運載火箭上升段軌跡快速優化研究［J］.宇航學報，2011，32(1):15-21.

［12］孫勇，段廣仁，張卯瑞，等.高超聲速飛行器再入過程改進氣動系統模型［J］.系統工程與電子技術，2011，33(1):134-137.

［13］Etkin B，Reid L D.Dynamics of flight-stability and control［M］.New York:John Wiley and Sons lnc，1995.

［14］Philip E G.SNOPT:an SQP algorithm for large-scale constrained optimization［J］.SIAM Review，2005，47(1):99-131.

［15］閆循良.基于空間發射的組合機動路徑規劃研究［D］.西安:西北工業大學，2011.

Rapid re-entry trajectory optimization for boost-glide missile

ZHAO Xin1，YAN Xun-liang1，ZHANG Jin-sheng1，WANG Shi-cheng1，HE An-rong2
(1.The Second Artillery Engineering University，Xi＇an 710025，China;2.The Military Deputy office of the Second Artillery in 211 Factory，Beijing 100084，China)

Rapid re-entry trajectory optimization of near space boost-glide missile was studied via the Legendre-Gauss-Lobatto(LGL)pseudospectral method.Firstly，an accurate mathematics model in re-entry phase was established based on an improved aerodynamic model.Aiming at the difficulties of the optimization problem in processing of aerodynamic data as well as optimization solving，the steps based on LGL pseudospectral method were listed systemically for solving the optimal re-entry flight trajectory.Then a serial strategy based on LGL pseudospectral method was presented to deal with the difficulties in optimization using the LGL pseudospectral method directly.Finally，the feasibility and the optimality of optimal result were validated by integral propagation method and covector mapping principle，respectively.Simulation results show that computational time required for optimizing one reentry trajectory is 3 ～4 s，and thus the computational efficiency is high.Path constrains and boundary constrains are well satisfied，and the precision of this trajectory optimization method is high.The rapid re-entry trajectory optimization with characteristics of multiple constraints，multiple variables and large sparsity is achieved.

near space;boost-glide missile;re-entry trajectory optimization;pseudospectral method;optimal control

V448.2

A

1006-2793(2012)04-0427-07

2012-04-09;

2012-07-09。

國家自然科學基金項目(60874093);863項目(2011AA7053016)。

趙欣(1984—)，男，博士，研究方向為飛行動力學及控制。E-mail:zhaoxin20062111@163.com

(編輯:崔賢彬)