PWM激勵下異步電機鐵耗等值電阻模型

羅富強 夏長亮, 喬照威 王慧敏 宋戰鋒

（1.天津大學電氣與自動化工程學院 天津 300072 2.天津工業大學電工電能新技術天津市重點實驗室 天津 300387）

1 引言

為了滿足以運行效率優化和轉矩性能優化等為目標的高性能控制算法的需求，異步電機等效電路中鐵耗等值電阻的準確建模是一個需要重點考慮的方面[1-3]。傳統的異步電機等效電路中，電機鐵耗表示為一個恒定阻值的電阻，它能夠準確反映額定工況下的電機鐵耗。但在變頻運行時，該模型不再能夠準確反映電機鐵耗變化[4,5]；另一方面，相對于正弦激勵，采用PWM 激勵將使電機鐵耗增大[6,7]，導致該模型的準確度進一步降低。因此，在采用PWM激勵的變頻驅動系統中，需要對電機鐵耗建立更加準確的等值電阻模型。

目前，諸多文獻已對該問題做了相關研究。文獻[8-10]通過實驗獲得不同頻率下電機鐵耗數據，進而利用數據擬合方法建立考慮運行工況時鐵耗等值電阻模型。這種方法能夠對一定運行范圍內鐵耗較好地估計，為了保證估計的精度，需要進行充足的鐵耗測量。文獻[11]將鐵耗模型細分為磁滯、經典渦流和異常渦流三個分量，它們隨頻率、磁通密度的變化規律各不相同。基于該模型，文獻[12]將磁滯損耗和渦流損耗分別表示為兩個等值電阻，并通過引入復數磁導率推導了這兩個電阻的表達式。該模型構建過程中需要知道與鐵磁材料相關的時間常數，但這些參數通常難以獲得。文獻[13,14]通過在電機等效電路中引入梯形網絡，計及鐵耗的非線性變化。該模型能夠動態地計算鐵耗各個分量。文獻[15,16]通過修正正弦激勵下鐵耗分離模型，得到PWM 激勵下鐵耗模型。該方法能夠有效提高PWM激勵下鐵耗計算精度，但無法直接應用于等值電路中鐵耗模型的構建。

本文基于鐵耗分離模型，利用三個等值電阻分別等效鐵耗的三個分量，根據功率平衡原理，推導了正弦激勵下鐵耗等值模型。通過分析PWM 激勵與正弦激勵下鐵耗等值電阻間的關系，得到PWM激勵下鐵耗等值電阻模型。為了確定模型中所需參數，提出了相應的實驗方案，該方案通過測量電機三個不同運行頻率下的鐵耗值實現。仿真和實驗結果驗證了本文提出模型的正確性和有效性。

2 正弦激勵下鐵耗等值電阻模型

2.1 鐵耗計算模型

根據Bertotti 建立的鐵耗分離計算模型，鐵耗由磁滯、經典渦流和異常渦流三個分量組成[11]

式中Pfe——總鐵耗；

Ph——磁滯損耗；

Pc——經典渦流損耗；

Pe——異常渦流損耗。

磁滯分量Ph取決于似穩狀態下磁滯環所包圍的面積和磁通密度交變的頻率，如下式所示

式中Kh——磁滯系數；

Gfe——鐵心質量；

f——磁通密度交變頻率；

Bm——磁通密度幅值；

x——斯坦梅茨系數。

經典渦流分量Pc、異常渦流分量Pe取決于磁通密度的變化率，分別通過下式計算

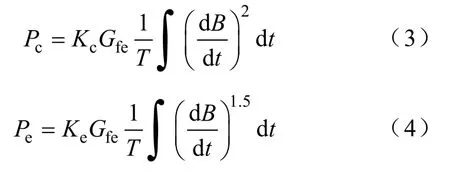
式中Kc，Ke——經典渦流、異常渦流系數；

B——磁通密度變化波形。

當磁通密度波形為正弦變化時，化簡式（2）～式（4），則鐵耗可表示為

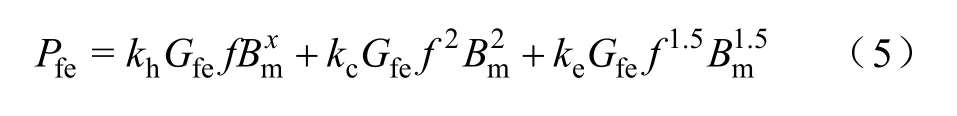
2.2 傳統鐵耗等值電阻模型

傳統的異步電機等效電路如圖1 所示，其中電機的鐵耗由電阻Rm表示，鐵耗計算式為

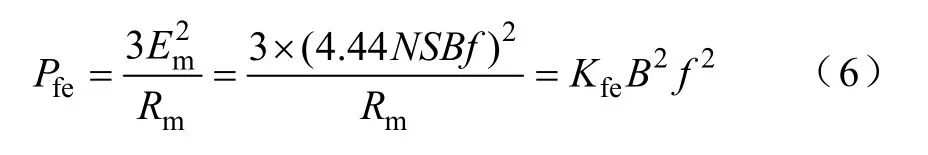
式中Em——激磁電動勢；

Rm——鐵耗等值電阻；

S——鐵心截面積；

N——每相繞組的匝數。

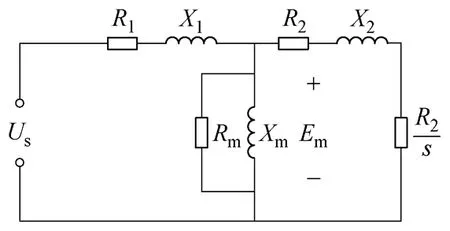
圖1 異步電機的等效電路Fig.1 Equivalent circuit of IM

由式（6）可知，若采用該等值電阻計算鐵耗，鐵耗計算值近似隨磁通密度和頻率乘積的二次方變化。由式（5）可知，總鐵耗中鐵耗各個分量隨磁通密度和頻率的變化規律各不相同，其中磁滯損耗隨磁通密度的x次方、頻率的一次方變化，經典渦流損耗隨磁通密度、頻率的二次方變化，異常渦流損耗隨磁通密度、頻率的1.5 次方變化。對比式（5）和式（6）可知，采用圖1 中等值電阻計算鐵耗時，其計算結果隨頻率、磁通密度的變化規律與經典渦流損耗相同。電機正常運行頻率范圍內，經典渦流損耗所占總鐵耗的比例相對磁滯損耗較小，且隨著頻率降低，該比例將進一步降低。因此，電機變頻運行狀況下，采用圖1 中鐵耗等值電阻計算電機的鐵耗將帶來較大的計算誤差。

2.3 改進的鐵耗等值電阻模型

由以上分析可知，為了提高電機變頻運行狀況下鐵耗的計算精度，需要考慮鐵耗各個分量隨磁通密度和頻率變化規律不同的影響，因此有必要為每個鐵耗分量分別等效一個電阻，則相應的異步電機等效電路如圖2 所示。

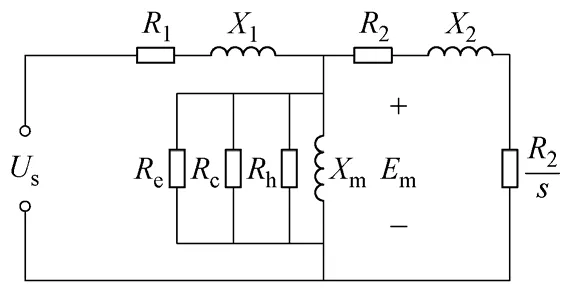
圖2 考慮鐵耗各個分量的異步電機等效電路Fig.2 Equivalent circuit of IM considering each component of the total iron loss

圖2 中，Rh、Rc和Re分別為表示磁滯損耗、經典渦流損耗和異常渦流損耗的等值電阻。根據等效電路，各損耗分量的計算如下

式中Im——勵磁電流；

Xm——勵磁電抗；

Lm——勵磁電感。

為了根據式（7）推導Rh、Rc和Re三個電阻的表達式，需要知道鐵耗的各個分量，本文基于鐵耗分離模型，推導這些量在等值電路中的表達方式。鐵耗分離模型描述了鐵磁材料中鐵耗隨磁通密度及頻率的變化關系，根據此模型計算鐵磁材料的鐵耗，需要知道磁通密度在鐵磁材料中的分布情況。由于電機定子鐵心內磁通密度非均勻分布，為了準確計算鐵耗，需要將電機鐵心分塊。一般地，若將電機鐵心分割為足夠小的n塊，則可認為每塊的磁通密度分布均勻，假設磁通密度的最大值為Bm、第i塊的磁通密度為Bi，且存在關系Bi=KiBm，則根據式（5），電機鐵耗各個分量為

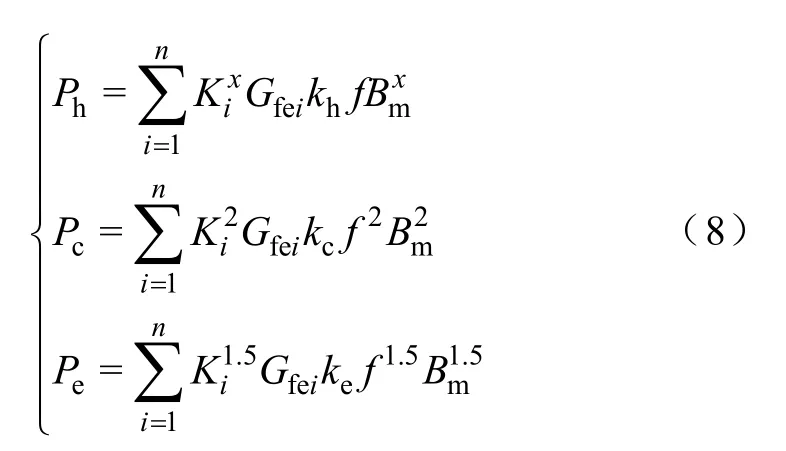
若忽略鐵磁材料飽和，則磁通密度幅值Bm與勵磁電流Im之間為線性關系，即

令式（7）和式（8）中鐵耗各個分量相等，并聯立式（9），則各個鐵耗等值電阻可表示為

由式（10）可知，改進后的模型中鐵耗各分量的等值電阻隨頻率及勵磁電流變化而變化，且變化規律各不相同。其中磁滯損耗電阻隨頻率的一次方、勵磁電流的2-x次方變化；經典渦流損耗電阻為恒值，不隨頻率、勵磁電流發生變化；異常渦流損耗電阻隨頻率和勵磁電流乘積的1.5 次方變化。各電阻分量的變化規律與鐵耗分離模型相同，因此采用式（10）計算電機的鐵耗，將能更加真實地反映鐵耗的實際變化情況。

3 PWM 激勵下鐵耗等值電阻模型修正

在非正弦激勵下，相對于正弦激勵，異步電機鐵耗隨輸入電壓波形的不同而發生變化，且其變化規律與輸入電壓波形存在緊密聯系。若忽略繞組損耗，則輸入電壓與磁通密度變化率的關系為

式中V——輸入電壓；

N——線圈匝數；

S——鐵心截面積。

若輸入電壓為PWM 波形，如圖3 所示，其幅值為Vm1，基波頻率為f，每半周期的脈沖數為p，第i個脈沖的寬度為τi，起始時間為ti。由式（11）可知，鐵心內磁通密度變化率為

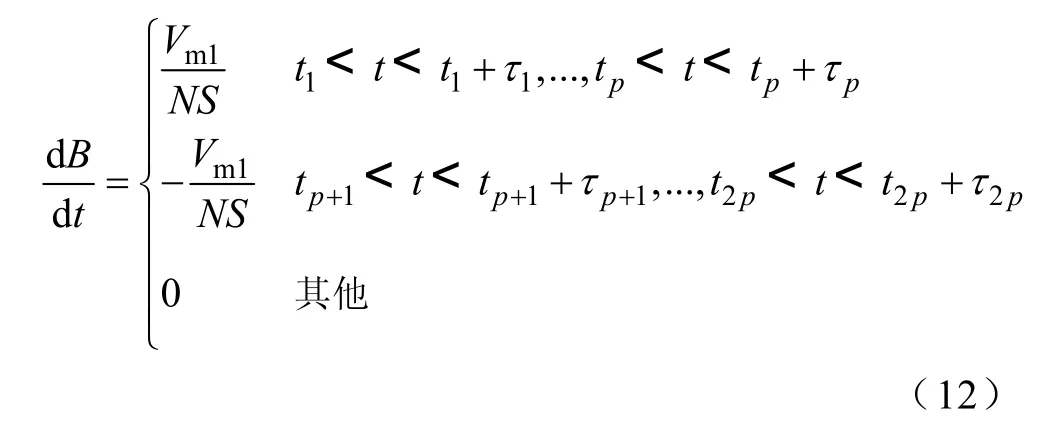
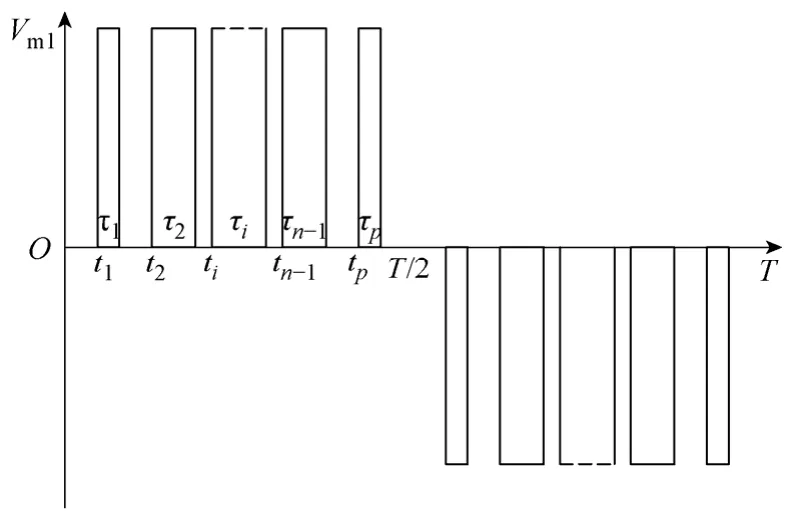
圖3 PWM 電壓波形Fig.3 Voltage waveform of PWM

將式（12）代入式（3），則PWM 激勵下經典渦流損耗為

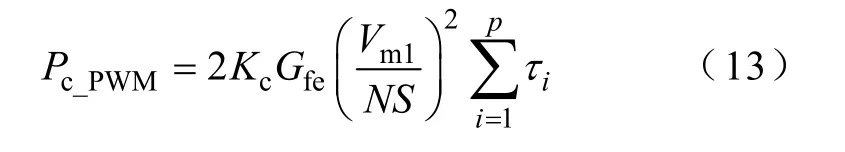
根據式（5），該PWM 波形中基波分量產生的經典渦流損耗為

式中Vm2——PWM 波形基波電壓幅值，且Vm2=mVm1，其中m為PWM 波形的調制 系數；

T——基波周期。

由PWM 波形的性質可知，其半周期脈沖寬度 之和、調制系數和基波周期存在關系：，則由式（13）和式（14）可得PWM 激勵下和其對應基波正弦電壓激勵下經典渦流損耗的關系為

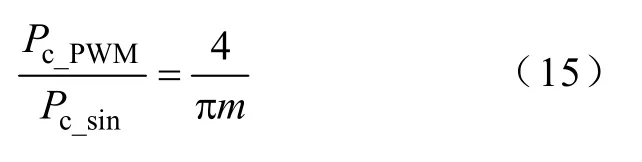
同理可得，兩種激勵下異常渦流損耗的關系為

由于兩種激勵下磁通密度幅值相等，則由式（2）可知，二者的磁滯損耗相等，即

式（15）～式（17）描述了PWM 激勵與正弦激勵下電機鐵耗間關系，由表達式可知，調制系數是影響PWM 激勵下鐵耗變化的主要因素。由于調制系數總是小于1，故相對于正弦激勵，PWM 激勵下鐵耗將增大，且增大部分由渦流損耗的增加造成。調制系數越低，鐵耗增大越多。

根據式（15）～式（17），在已知正弦激勵下鐵耗各個分量時，可得到PWM 激勵下鐵耗值。據此對式（10）中鐵耗等值電阻進行修正，則其表達式為

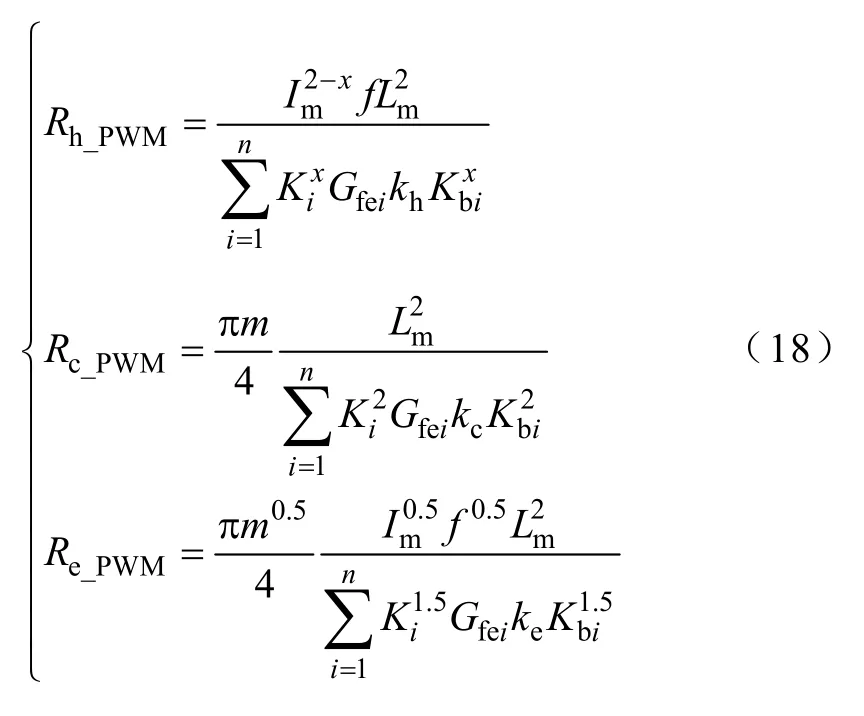
4 模型參數確定

為了使用以上模型計算電機的鐵耗，需確定模型中參數。由于鐵耗分離模型系數及幾何參數通常難以預先獲取，給模型參數的直接計算造成困難，為此，本文提出一個確定模型所需參數的實驗方案，步驟如下：

（1）分離額定狀況下總鐵耗為磁滯損耗、經典渦流損耗和異常渦流損耗分量。

鐵耗各個分量隨磁通密度和頻率的變化規律各不相同，因此通過測量不同磁通密度、頻率下鐵耗值，可將總鐵耗分離為各個分量。由于電機正常運行條件下磁通密度近似保持不變，因此分離過程中可只考慮頻率對鐵耗的影響。空載條件下，分別測量頻率為f1、f2和f3，同時保持定子電流為額定勵磁電流情況下的鐵耗，分別為Pfe1、Pfe2和Pfe3。由于定子電流相同，則磁通密度幅值相同，因此根據式（8）可得

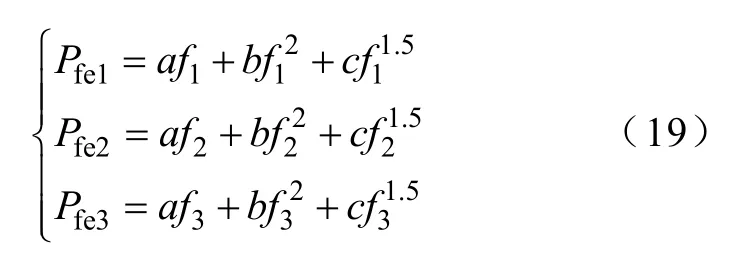
根據式（19），運用最小二乘法，可解得a、b和c，則額定頻率fN下鐵耗的各個分量為

（2）計算額定狀況下各個鐵耗等值電阻分量。

在計算出鐵耗各個分量后，根據圖2，空載條件下，可得額定頻率下各個鐵耗等值電阻為

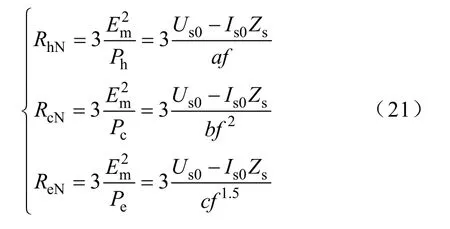
式中Us0——空載輸入電壓；

Is0——空載定子電流；

Zs——定子阻抗。

（3）計算任意頻率、勵磁電流條件下各個鐵耗等值電阻分量。

對式（10）重新整理，可得

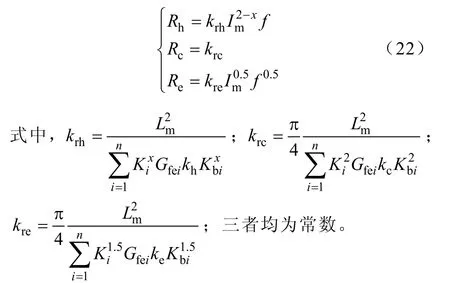
聯立式（21）、式（22）和式（18）可得任意運行條件下鐵耗等值電阻為

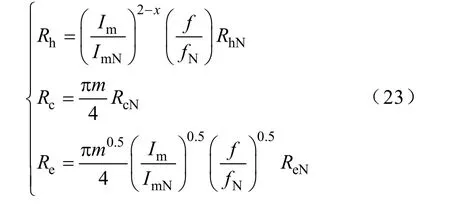
式（23）描述了各個鐵耗等值電阻分量在任意頻率、調制系數下的變化規律。

特別地，若頻率、調制系數二者的變化存在聯系，如調制系數隨頻率成正比變化，則式（23）可寫為

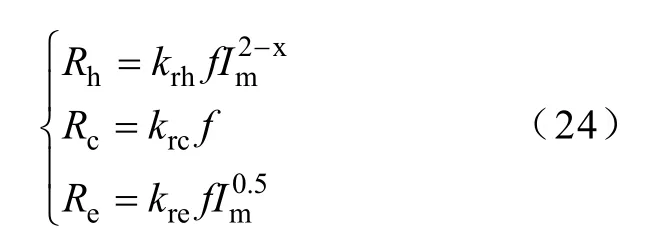
由于電機正常運行狀況下Im變化較小且異常渦流損耗分量占總損耗的比例較小，因此若忽略Im的影響，則鐵耗等值電阻的各個分量將均隨頻率成正比變化，因此三者可合并為一個電阻，如下式所示

此時，確定模型參數無需進行鐵耗分離，鐵耗等值電阻可采用傳統的鐵耗測量方法確定，即通過空載實驗計算鐵耗等值電阻。與傳統鐵耗等值電阻不同，該模型中鐵耗等值電阻隨頻率成正比變化，同時計及調制系數的影響，而傳統鐵耗等值電阻則保持不變。

5 仿真與實驗驗證

5.1 仿真驗證

為驗證改進的鐵耗等值電阻模型的有效性，分別利用傳統模型和改進模型，對一臺11kW 異步電機的鐵耗進行仿真計算，并將計算結果與Ansoft 有限元分析的結果進行對比。異步電機參數見下表。

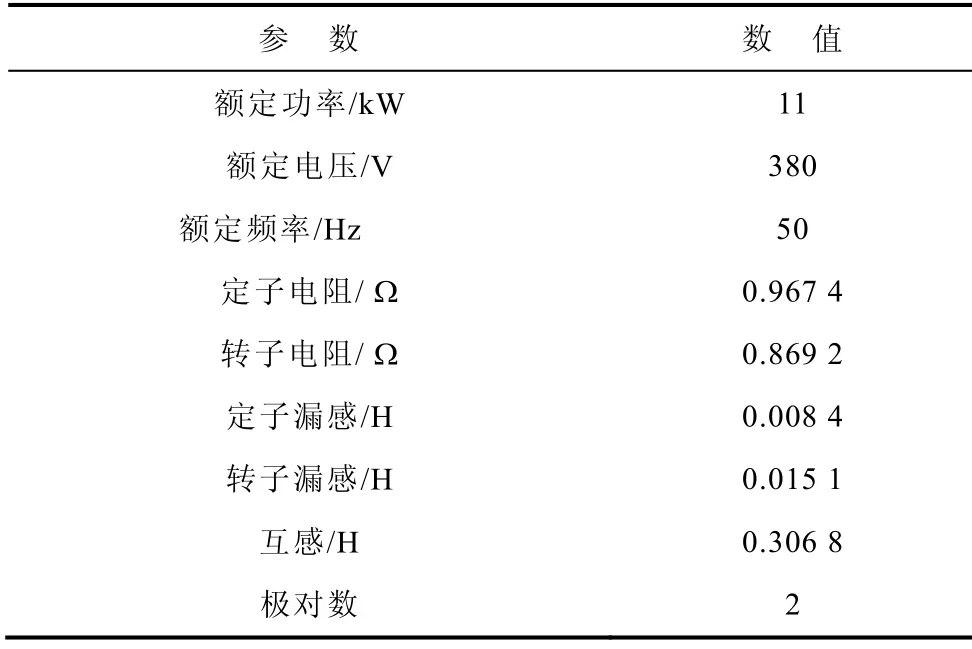
表 異步電機參數Tab. Parameters of IM

利用有限元法在三個不同頻率下的鐵耗計算結果，根據第4 節中模型參數確定方法，空載條件下，頻率為50Hz 時，改進模型中各個鐵耗等值電阻計算值Rh0為1 801Ω，Rc0為8 101Ω，Re0為∞Ω，此時傳統等值電阻為1 473Ω。

將圖2 所示等效電路中三個鐵耗等值電阻表示為一個總鐵耗等值電阻，當電機由PWM 激勵，勵磁電流保持不變時，該等值電阻與頻率、調制系數的關系如圖4 所示。

圖4 總鐵耗等值電阻Fig.4 Total equivalent resistance of iron loss

由圖4 可知，改進后的總鐵耗等值電阻隨頻率和調制系數變化而變化，頻率、調制系數越小，總鐵耗等值電阻越小。而傳統鐵耗等值電阻則一直保持不變。由圖4 還可看出，隨著頻率的減小，調制系數對鐵耗等值電阻的影響變小，因為調制系數只影響渦流損耗的變化，而頻率降低時渦流損耗占總鐵耗的比例降低。

圖5 為正弦激勵下，采用改進方法和傳統方法的鐵耗計算結果。

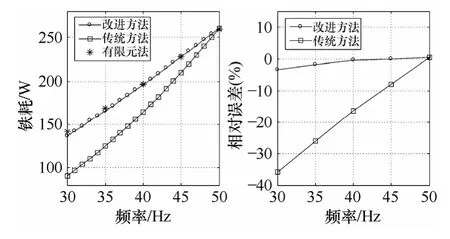
圖5 正弦激勵下兩種方法的鐵耗計算結果Fig.5 Comparison of iron loss calcultion results under sinusoidal excitation

由圖5 可知，傳統方法能以較高精度計算電機額定頻率運行時的鐵耗，但電機運行于較低頻率時，其鐵耗計算將出現較大偏差，且頻率越低，偏差程度越大。當頻率為30Hz 時，其計算結果相對于有限元法的誤差為35.2%。改進方法則能以較高精度計算各運行頻率下電機鐵耗，頻率為30Hz 時，其計算結果相對于有限元法的誤差為3.6%，比傳統方法提高了31.6%。正弦激勵下，改進方法有效提高了鐵耗計算的準確度。

圖6 為正弦激勵和PWM 激勵下，有限元法的鐵耗計算結果。

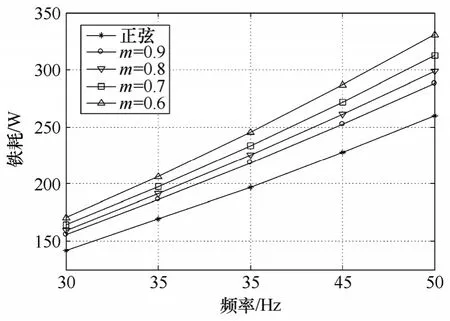
圖6 正弦激勵和PWM 激勵下有限元法鐵耗計算結果Fig.6 Iron loss caculation results under sinusoidal and PWM excitation

由圖6 可看出，與正弦激勵相比，PWM 激勵下，電機的鐵耗增加。同時，隨調制系數降低，電機的鐵耗增大，頻率為50Hz、調制系數為0.6 時，相對于正弦激勵，鐵耗增大26.9%。

圖7 為PWM 激勵下，采用改進方法和傳統方法在不同調制系數下的鐵耗計算結果。

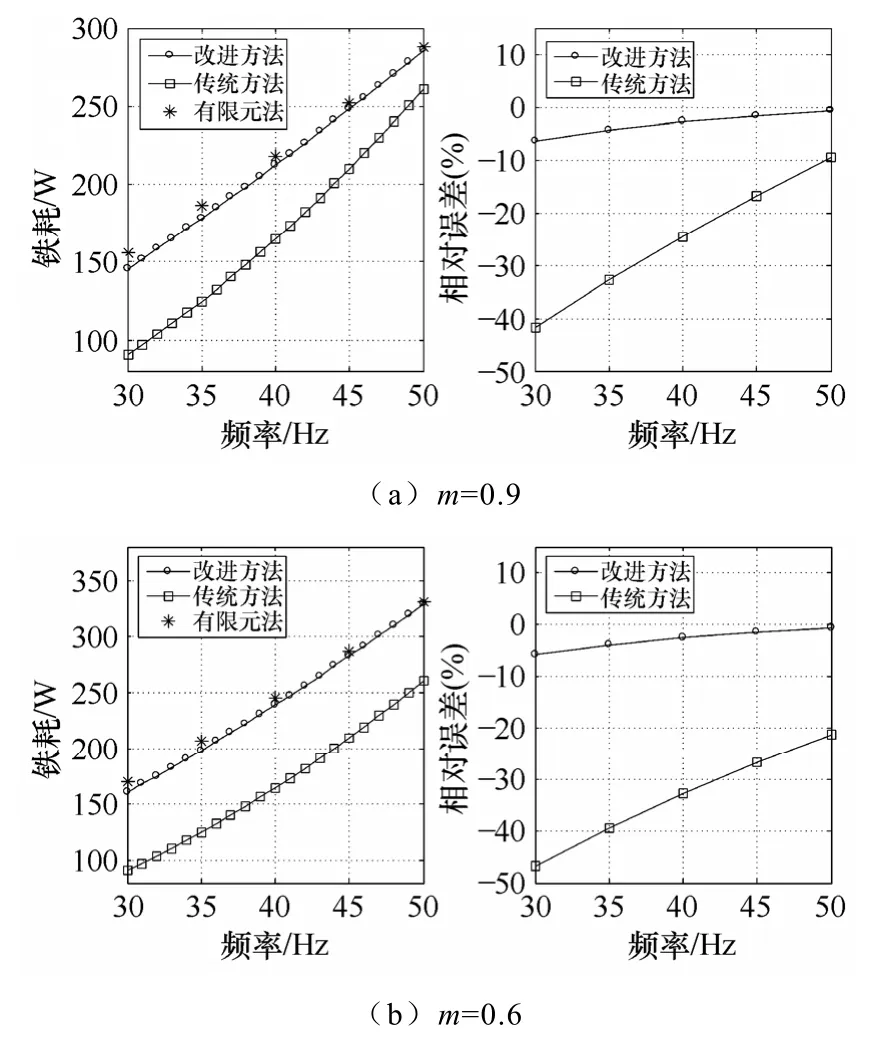
圖7 PWM 激勵下兩種方法的鐵耗計算結果Fig.7 Comparison of iron loss under PWM excitation

由圖7 可以看出，改進方法在不同頻率、不同調制系數下，均能以較高精度計算電機鐵耗，其相對誤差保持在7%以內，傳統方法則存在較大誤差。另外，相對于正弦激勵，由于傳統方法未計及調制系數的影響，其計算誤差進一步增大，在額定頻率下，將產生10.0%～21.2%的相對誤差，這部分誤差是由PWM 激勵下鐵耗的增加造成。由圖7 還可以看出，傳統方法的計算誤差隨調制系數的減小而增大，調制系數為0.6、頻率為30Hz 時，其計算誤差為47.2%，而此時改進方法的計算誤差為6.8%，相對于傳統方法降低了40.4%。

5.2 實驗驗證

對一臺采用恒壓頻比控制的異步電機的鐵耗進行了實驗測量。電機額定功率為1.1kW，額定電壓為380V，額定頻率50Hz，額定功率因數為0.6。為了測量PWM 激勵下鐵耗的增加以及提高測量準確度，實驗中使用示波器觀測電機定子輸入電壓、電流及瞬時功率波形。電機空載條件下，電壓為380V、頻率為50Hz 時，定子電流、輸入電壓和瞬時功率的實驗測量波形如圖8 所示，此時電機的鐵耗測量結果為114W。

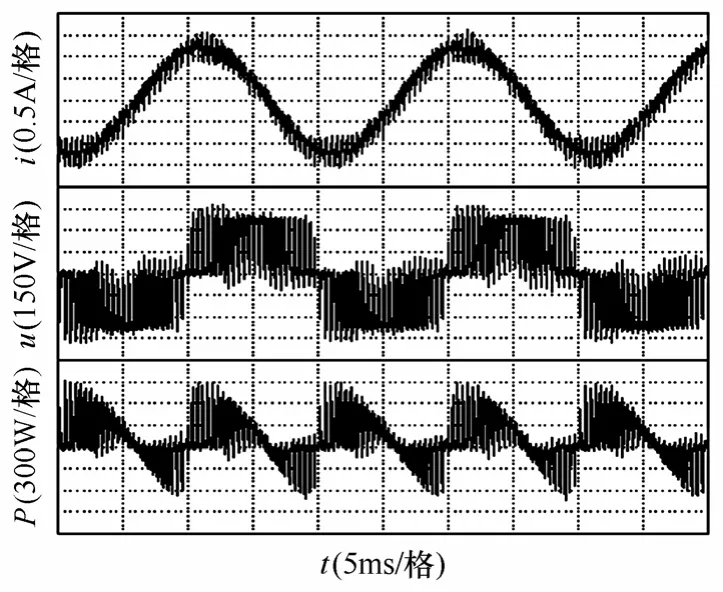
圖8 實驗測量波形Fig.8 Measured waveforms by experiment

恒壓頻比控制下，由于調制系數隨電壓成正比變化，其也將隨頻率成正比變化。因此，根據式（25），此時的鐵耗等值電阻為3767 Ω，則此控制方式下，兩種方法的鐵耗計算結果及其與實驗測量值的對比如圖9 所示。

圖9 恒壓頻比控制下兩種方法的鐵耗計算結果Fig.9 Comparison of iron loss under constant V/F control

由圖9 可知，兩種方法均能在額定頻率下以較高精度計算鐵耗。隨著頻率降低，兩種方法的計算精度均有所降低，但對比圖中變化曲線可以看出，二者的計算精度不同。由于改進模型中，鐵耗等值電阻隨頻率按照式（25）變化，而傳統模型中鐵耗等值電阻保持不變，因此，改進方法相對于傳統方法有較高的計算精度，在頻率為30Hz 時，相對于傳統方法，提高了29.8%。造成改進方法在頻率降低時計算誤差增大的原因可能為：頻率降低時鐵耗的測量值相對偏高。實驗中鐵耗的測量值為實際鐵耗與雜散損耗之和，在實驗測量條件下，電機的負載保持不變，故雜散損耗不隨頻率發生變化[17]，而鐵耗隨頻率減小而減小。因此頻率降低時，鐵耗實際值占鐵耗測量值的比例將減小，從而使鐵耗的測量值偏高。

6 結論

本文建立了PWM 激勵下異步電機的鐵耗等值電阻模型，模型中采用三個變化的電阻等效電機的鐵耗，從而計及鐵耗的非線性變化。其中，運行頻率降低和調制系數減小均將導致鐵耗等值電阻減小。仿真和實驗結果表明，改進模型有效提高了鐵耗的計算精度，較為真實地反映了電機鐵耗的變化規律，為建立更加準確的電機仿真模型打下了較好的基礎。

[1]Bijan Zahedi,Sadegh Vaez Zadeh.Efficiency optimization control of single-phase induction motor drives[J].IEEE Transactions on Power Electronics,2009,24(4):1062-1071.

[2]Nasir M Uddin,Sang Woo Nam.New online loss-minimization-based control of an induction motor drive[J].IEEE Transactions on Power Electronics,2008,23(2):926-933.

[3]崔納新,張承慧,呂志強,等.基于電壓空間矢量的電動汽車電驅動系統高效快轉矩響應控制[J].電工技術學報,2009,24(3):61-66.Cui Naxin,Zhang Chenghui,Lü Zhiqiang,et al.Fast torque response control of high efficiency drives in electric vehicles based on voltage space vector[J].Transactions of China Electrotechnical Society,2009,24(3):61-66.

[4]Kirschen D S,Novotny D W,Suwanwisoot W.Minimizing induction motor losses by excitation control in variable frequency drives[J].IEEE Transactions on Industry Applications,1984,IA-20(5):1244-1250.

[5]Jian T,Schmitz N,Novotny D.Characteristic induction motor slip values for variable voltage part load performances optimization[J].IEEE Transactions on Power Apparatus and Systems,1983,PAS-102(1):38-46.

[6]Boglietti A,Ferraris P,Lazzari M,et al.Influence of modulation techniques on iron losses with single phase DC/AC converters[J].IEEE Transactions on Magnetics,1996,32(5):4884-4886.

[7]Boglietti A,Cavagnino A,Lazzari M,et al.Predicting iron losses in soft magnetic materials with arbitrary voltage supply:an engineering approach[J].IEEE Transactions on Magnetics,2003,39(2):981-989.

[8]王建淵,安少亮,李潔,等.考慮主磁路飽和與鐵損的異步電機模型[J].電工技術學報,2010,25(10):44-50.Wang Jianyuan,An Shaoliang,Li Jie,et al.Modeling of induction motor considering main flux saturation and iron loss[J].Transactions of China Electrotechnical Society,2010,25(10):44-50.

[9]Moulahoum S,Touhami O.An approach to an induction machine modeling in presence of saturation and iron loss[C].IEEE Power Engineering Society General Meeting,2005:2272-2276.

[10]Emil Levi,et al.Iron loss in rotor-flux-oriented induction machines:identification,assessment of detuning,and compensation[J].IEEE Transactions on Power Electronics,1996,11(5):698-709.

[11]Bertotti G.General properties of power losses in soft ferromagnetic materials[J].IEEE Transactions on magnetic,1988,24(1):621-630.

[12]Buecherl D,Herzog H.Iron loss modeling by complex inductances for steady state simulation of electrical machines[C].International Symposium on Power Electronics Electrical Drives Automation and Motion(SPEEDAM),2010:878-883.

[13]Hui S Y R,Zhu J.Numerical modelling and simulation of hysteresis effects in magnetic cores using transmission-line modelling and the Preisach theory[J].IEE Proceedings Electric Power Applications,1995,142(1):57-62.

[14]Hui S Y R,Zhu J G,Ramsden V S.A generalized dynamic circuit model of magnetic cores for low-and high-frequency applications II.circuit model formulation and implementation[J].IEEE Transactions on Power Electronics,1996,11(2):251-259.

[15]Amar M,Kaczmarek R.A general formula for prediction of iron losses under nonsinusoidal voltage waveform[J].IEEE Transactions on Magnetics,1995,31(5):2504-2509.

[16]Gmyrek Z,Boglietti A,Cavagnino A.Estimation of iron losses in induction motors:calculation method,results and analysis[J].IEEE Transactions on Industrial Electronics,2010,57(1):161-171.

[17]Boglietti A,Cavagnino A,Ferraris L,et al.Induction motor equivalent circuit including the stray load losses in the machine power balance[J].IEEE Transactions on Energy Conversion,2008,23(3):796-803.