基于分形理論的混凝土大壩結冰變徑模型設想

楊 帆，謝明宇

(1．遼寧建筑職業技術學院，遼寧 遼陽 111000;2．遼陽供電公司，遼寧 遼陽 111000)

很多地區水電站大壩深受混凝土抗凍性差問題的困擾。例如云峰水電站，在大壩建成并投入運行的幾年里，溢流壩表面混凝土凍融破壞面積高達1 000 m2，占整個溢流壩面積50%左右，混凝土平均凍融剝蝕深度達10 cm以上。大型混凝土結構工程的抗凍性分析往往建立在大量實驗數據基礎上，若能利用理論達到預測目的，并判斷出孔隙水瞬間結冰孔徑范圍，則可以人為調節孔徑大小，提高混凝土大壩等大型混凝土結構工程抗凍能力。

混凝土內部孔隙結構通常是不規則、無序分布、千奇百怪的，不像傳統假設那樣光滑、平直、等大、規則，材料孔形、面積、體積等在各個尺度上均表現出分形特征。在以往的水泥混凝土材料研究中，滲透性孔隙模型多假設為平滑圓柱孔，而且是直線型的，但實際上孔隙是彎曲、復雜的非平滑表面。為描述其彎曲復雜程度，國外已有學者采用4次Koch曲線模型評價孔隙特征，并通過試驗確定了相似維數，使評價更科學合理［1］。

本文將混凝土大壩看作是具有分形結構的空間載體，研究其內部孔隙分形特征，分析孔隙復雜程度及對混凝土大壩結構孔隙水過冷度的影響。同時引入分形理論，根據混凝土材料內部孔隙結構特征，從討論單位橫截面積A0上孔隙直徑r分布入手，引入孔隙分布分形維數D以及孔隙通道彎曲分形維數Dτ，得出有關分形孔隙孔隙水過冷度的公式。

1 混凝土凍融破壞機理

混凝土在凍融過程中，遭受的破壞應力主要由兩部分組成。其一，混凝土中毛細孔水在某負溫下發生物態變化，由水轉變成冰，體積膨脹9%，因受毛細孔壁約束形成膨脹壓力，在孔周圍微觀結構中產生拉應力;其二，當毛細孔水結成冰時，由凝膠孔中過冷水在混凝土微觀結構中遷移和重分布引起滲管壓。由于表面張力作用，混凝土毛細孔隙中水的冰點隨著孔徑減小而降低。當膠凝孔水形成的冰核溫度在－78℃以下時，由冰與過冷水飽和蒸汽壓差和過冷水之間鹽分濃度差引起水分遷移而形成滲透壓。另外膠凝不斷增大，形成更大的膨脹壓力，當混凝土受凍時，這兩種壓力會損傷混凝土內部微觀結構，經過反復凍融循環以后，損傷逐步積累、不斷擴大，發展成互相連通的裂縫，使混凝土強度逐步降低至完全喪失，混凝土表面開始剝落甚至整體破壞。

2 變徑理論

2.1 變徑理論的提出設想

混凝土材料受凍融破壞主要是由孔隙中水結冰所致。水結冰時體積增大約9%，若混凝土材料孔隙中充滿水，則結冰膨脹對孔壁產生很大應力，當此應力超過材料抗拉強度時，孔壁局部開裂。隨著凍融次數增多，材料破壞加重。

混凝土材料抗凍性取決于孔隙率、孔隙特征及充水程度。若孔隙不充滿水，即遠未達到飽和，具有足夠自由空間，即使受凍也不致產生很大凍脹應力。極細的孔隙，雖可充滿水，但因孔壁對水吸附力極大，吸附在孔壁上的水冰點很低，在一般負溫下不會結冰;粗大孔隙一般水分不會充滿其中，對凍脹破壞可起緩沖作用;閉口孔隙水分不能滲入;毛細管孔隙既易充滿水分，又能結凍，故對材料冰凍破壞作用影響最大。

當溫度降至冰點以下時，由于混凝土中水分大部分已結冰，水泥顆粒不能與冰發生化學反應，混凝土強度停止發展，孔隙內水分結冰會引起膨脹(水結凍體積可膨脹約9%)，作用在孔隙毛細管內壁，破壞混凝土內部結構，已經獲得強度 (在結冰前混凝土已不同程度硬化)受到損失。當氣溫忽高忽低反復凍融，混凝土內部微裂逐漸增長、擴大，強度逐漸降低，表面出現剝落，甚至完全崩潰。

混凝土內部結冰從微觀上分析是一個類似隨機過程，并不是所有孔隙中水在零下時候都結冰。如圖1所示。

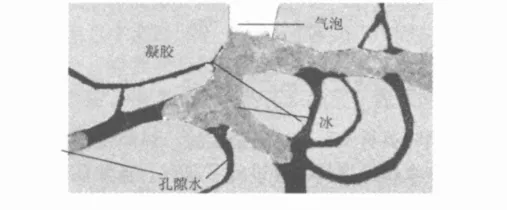
圖1 孔徑水結冰

飽和硬化水泥漿中蒸發水由于溶解氫氧化物的原因，不會在0℃時凍結，而凍結一旦開始，純冰從溶液中析出，溶液濃度提高，冰點進一步下降，在不摻鹽類的水泥漿體中自由水冰點約為－1.5～－1℃。由于孔隙表面張力的作用，不同孔徑孔內水飽和蒸氣壓與冰點不同，孔徑越小，孔內水飽和蒸氣壓越小，冰點越低。當環境溫度降低到－1.9～－1℃時，混凝土孔隙中水由大孔開始結冰，并逐漸擴展到小孔。一般溫度在－12℃時，毛細孔都能結冰，而凝膠孔中水分子物理吸附于水化水泥漿固體表面，在－78℃以上不會結冰。因此在某一固定負溫下水泥石中水分只有一部分是可凍水。有些孔隙中過冷水到－78℃才會凍結，且為一個瞬間過程，是瞬時反應。過冷水通過孔隙時結冰與否由孔徑決定，孔徑大小是能否瞬間結凍的關鍵。若是可以運用理論分析判斷出孔隙水瞬間結冰孔徑范圍，則可以人工調節孔徑大小，提高混凝土材料抗凍能力。

孔隙水是否會結冰是個十分復雜的問題。負溫條件下，過冷水通過飽和硬化水泥漿內部孔隙時，可能會因為孔徑變化而突然結冰，也可能并未對過冷水過冷度產生影響。

根據研究，引用分形理論研究混凝土內部孔隙結構圖可描述出孔隙特征，見圖2。

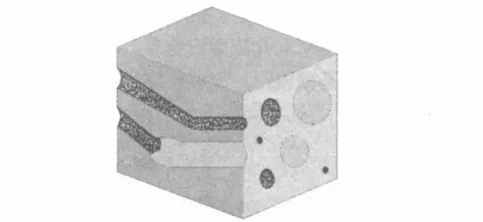
圖2 分形孔隙孔徑水結冰模型

2.2 具有分形結構的混凝土孔隙結冰

2.2.1 分形

分形學 (Fractal)是由Mandelbrot于1976年首次提出來的。分形的原意是“不規則的、分散的、支離破碎的”物體。

分形理論所研究對象主要是復雜、不規則、具有自相似性的幾何形體。分形結構幾何體具有以下性質［2］:

a． 具有精細結構，即在任意小尺度下都具有復雜結構;

b． 具有不規則性，整體與局部不能用傳統幾何語言來描述;

c． 具有自相似形式，可是近似的或統計意義的;

d． 通常分形圖形在某種意義下維數大于其拓撲維數;

e． 在大多數情況下，分形圖形可用非常簡單的方法產生。

分形圖形的最基本特征是自相似性和標度不變性。所謂自相似性是指某種結構或過程特征從不同空間或時間尺度來看都是相似的，或者某系統或結構局部性質或局部結構與整體類似。標度不變性是指，從分形圖形上任選一個局部區域，無論放大或縮小，它的形態、復雜程度、不規則性等各種特性均不會發生變化，所以標度不變性又可稱為伸縮對稱性。表征這2種分形性質的定量參數為分形維數(Fractal Dimension)，用來描述一個復雜系統的復雜、不規則程度，為整數或非整數都可，并有多種定義和測定方法。

2.2.2 混凝土孔隙分布分形維數

研究影響混凝土滲透性的介觀孔隙通道 (即沒有分支的通道，它與孔網格中2個近鄰位相連接，孔隙通道兩端可都開口，也可一端開口，一端封閉)，其軸線為彎曲、復雜曲線，具有分形特征。

混凝土孔隙分布同樣具有分形特征，假定孔隙分形分布在空間基本均勻。圖3是正方形單位截面A0上孔隙直徑為r的孔隙面積分布。

根據分形基礎理論，分形孔隙直徑大于r時累積數目N(r)與孔徑有如下關系:

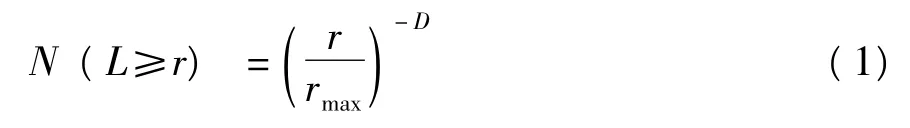
式中，r為孔隙直徑，cm;D為孔隙分布的分形維數，參考長度L∈ ［rmin，rmax］，rmin、rmax分別為單位截面上最小、最大孔隙直徑，cm。

對式 (1)進行r微分可得:

式中，表示直徑在 r和 r+dr之間的孔隙數目－dN＞0。

2.2.3 混凝土孔隙通道屈曲分形維數

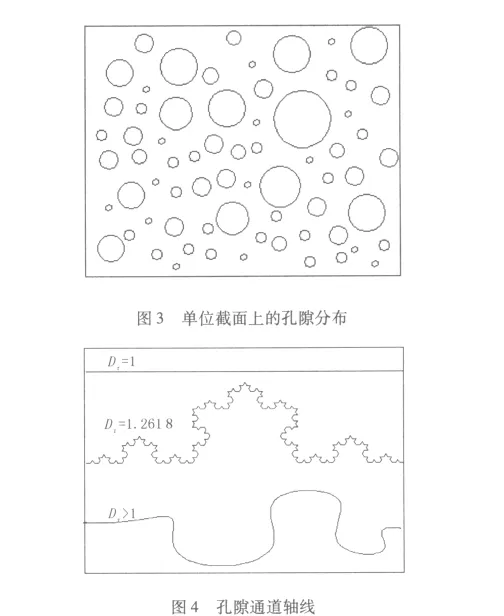
混凝土孔隙通道形狀是彎曲的，孔隙軸線是具有分形性質的復雜曲線。如圖4所示，孔隙通道軸線分別為直線、科赫曲線和無規分形曲線。引入孔隙路徑的屈曲分形維數Dτ衡量孔隙通道彎曲復雜度。圖4中，直線Dτ=1，科赫曲線Dτ=1.261 8，無規分形曲線Dτ＞1。

Yu［3］提出了毛細管長度和直徑之間指數關系，可以用于分析混凝土連通孔:

式中:Lτ(r)為孔隙直徑為r的孔隙通道長度，cm;Dτ為孔隙通道屈曲分形維數;L0為孔隙通道外觀長度，cm。

1≤Dτ＜2，當 Dτ=1時，孔隙通道為直線，此時 Lτ(r) =L0。

孔隙直徑在r和r+dr之間的孔隙體積微元dVp為

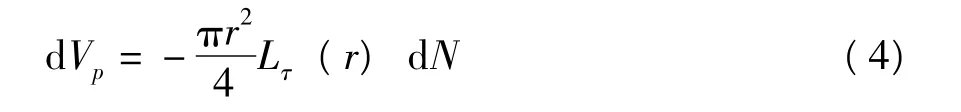
式中，Lτ(r)為孔隙直徑為r的孔隙通道長度，cm。

結合式 (3)和式 (4)得到:

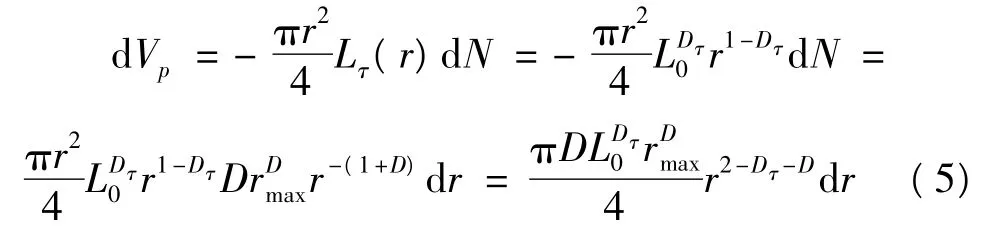
微分得到混凝土孔隙體積為

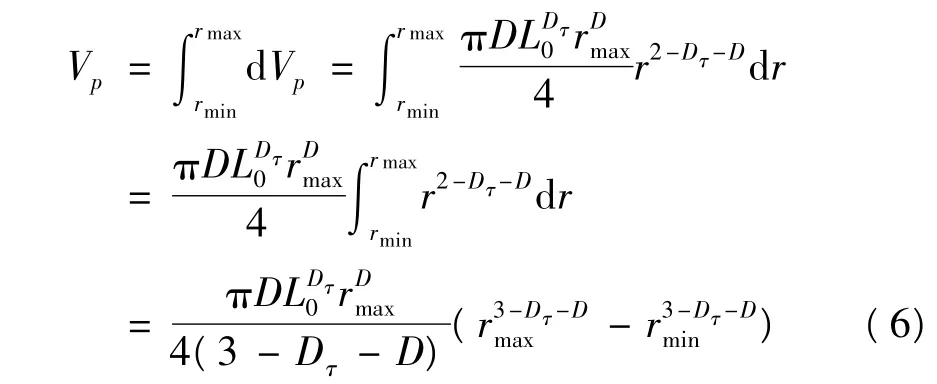
稻葉英男［4－6］通過大量實驗，對靜止情況下影響過冷水過冷度的因素進行了研究。齋藤認為，在外界條件一定時，發生結冰不是一個確定事件，可用概率描述發生結冰與過冷度之間關系。

在對大量實驗進行分析后，得到了過冷度與體積關系為

式中，ΔTm為過冷度，K;V為體積，cm3。

利用分形模型模擬混凝土材料孔隙特征，得到評價孔徑與孔隙水過冷度間關系，對研究如何提高混凝土材料抗凍性有很好指導意義。

通過研究模擬結果和積累實驗數據，得到過冷度與孔徑范圍的關系，可人為控制混凝土孔徑大小，從而提高混凝土抗凍性和耐久性，具有很好的經濟意義。

3 結論

a． 混凝土結冰從微觀上分析是一個類似隨機的過程，并不是所有孔隙中水在零下時候都結冰，有些孔隙中過冷水到－78℃才會凍結。孔隙中水結冰是個瞬間過程，是瞬時反應，在多大孔徑內瞬間結冰是關鍵。

b． 混凝土材料內部孔隙結冰過程:凝膠孔→變徑水 (過冷水)→瞬間結冰。零下狀態下，由于混凝土材料內部孔隙孔徑、結冰與否、過冷水過冷度不同。有些過冷水過冷度較大，造成凍害大，損害混凝土構件;而有些過冷水過冷度較小，不會凍結和進一步凍害混凝土材料。

c． 引用分形理論模擬混凝土材料內部孔隙特征，提出變徑理論，建立假想模型，為進一步提高混凝土抗凍性作出理論鋪墊。

［1］ 唐 明，王甲春，李連君．壓汞測孔評價混凝土材料孔隙分形特征的研究［J］．沈陽建筑工程學院學報，2001，17(4):272－275．

［2］ 孫洪軍，趙麗紅．分形理論的產生及其應用 ［J］．遼寧工學院學報，2005，25(2):113－117．

［3］ Yu B M．Cheng P．A fractal permeability model for bi-dispersed porous media．Int J Heat and Mass Transfer ［J］．2002，(45):19－21．

［4］ 稻葉英男，武谷健吾，野津茲．流動過冷卻水によろ連■制冰に閿する研究［C］．日本機械學會論文集，1992，58(548):1321．

［5］ 稻葉英男，武谷健吾，野津茲．靜止狀態におけるルク狀水および水溶液の過冷卻現象に影響を及ぼす諸因子の效果 ［C］．日本機械學會論文集，1993，59(560):1202．

［6］ 稻葉英男，武谷健吾．靜止水の過冷卻現象ぼす諸因子の影響［C］．日本機械學會論文集，1993，59(567):3557．