Stu rm-Liouv ille問題的特征值對勢函數的依賴性
張婷婷,魏廣生
(陜西師范大學數學與信息科學學院,陜西 西安 710062)
Stu rm-Liouv ille問題的特征值對勢函數的依賴性
張婷婷,魏廣生
(陜西師范大學數學與信息科學學院,陜西 西安 710062)
研究了定義在[0,1]上的Sturm-Liouville問題的特征值對勢函數的連續依賴性.應用比較定理和定義區間單調性證明了:當部分區間[x0,1]上的勢函數趨于無窮大時,[0,1]區間上的特征值漸進趨近于[0,x0]區間上的某個特征值.推廣了一些作者對Sturm-Liouville問題研究的相應結果,并為其相應問題的研究提供了一個新的視角.
勢函數;特征值;比較定理
1 引言
本文的動機由文獻[1-3]的工作所驅動.他們考慮了Sturm-Liouville(SL)問題的特征值依賴邊界,邊值條件以及勢函數的變化問題.所以SL問題是由微分方程:
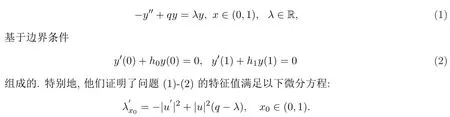
另外,他們還研究了當勢函數q,邊界條件和一個端點都固定時,SL問題的特征值和特征函數對另一個端點的依賴性.即當區間長度向零收縮時,最小的Dirichlet特征值趨于無窮大,但這一結論對于最小的Neum ann特征值并不成立,因為他是一個有限極限.其后對SL問題的研究涌現出大量推廣性結論[4-7].
本文考慮上述問題(1)-(2)的特征值關于部分區間[x01]上的勢函數變化問題,證明了與其平行性的結論:當[x01]區間上的勢函數趨于正無窮或負無窮大時,問題(1)-(2)的[0,1]區間上的特征值漸進趨于[0,x0]上的某個特征值;并進一步證明了上述問題(1)-(2)的[0,1]區間上的第m個特征值漸進趨近于[0,x0]上的第m個特征值.
2 定理及證明




[1] Kong Q, Zettl A. Dependence of eigenvalues of Sturm-Liouville problems on the boundary[J]. Differential Equations, 1996,126:389-407.
[2] Kong Q, Zettl A. Eigenvalues of regular Sturm-Liouville problems[J]. Differential Equations, 1996,131:1-19.
[3] Kong Q, Zettl A. Linear ordinary differential equations in Inequalities and Applications"[J]. WSSIAA, 1994,3:381-384.
[4] Kong Q, Wu H, Zettl A. Dependence of the nth Sturm-Liouville Eigenvalue on the problem[J]. Differential Equations, 1999,156:328-354.
[5] Kong Q, Wu H, Zettl A. Dependence of eigenvalues on the problem[J]. Nachr. Math., 1997,188:173-201.
[6] Zettl A. Sturm-Liouville Problems in Spectral Theory and Computational Methods of Stur-Liouville Prob-lems"[M]. New York: Dekker, 1997.
[7]李麗,黃振友.一類Schr¨odinger算子的譜范圍[J].純粹數學與應用數學,2011,27(3):387-391.
[8] Evitan B M. On the determination of a Sturm-Liouvillle equation by two spectra[J]. Mat. Tidskr., 1949,B:25-30.
[9] Paul Phillips D. A partial inverse Sturm-Liouville problem: Matching a step function potential to a finite eigenvalue list[J]. Math. Anal. Appl., 2005,312:248-260.
[10] Chavel I. Eigenvalues in Riemannian Geometry[M]. Orlando: Academic Press, 1984.
Dependence of eigenvalues of Sturm-Liouville problems on the potential function
Zhang Tingting,WeiGuangsheng
(College of Mathematics and Information Science,Shaanxi Normal University,X i′an 710062,China)
This paper studiesmain ly the eigenvalues of Sturm-Liouville(SL)p roblem s def nded in[0,1]dependent continously on the potential function.By the com parison theorem and domainmonotonicity,it proves that when the potential function in the interval[x0,1]tends to in fnity,the eigenvalues in the interval[0,1]asym ptotically app roach the eigenvalues in the interval[0,x0].It promotes the corresponding results of Sturm-Liouville problems which some authors studies, and provides a new angle of view.
potential function,eigenvalue,comparison theorem
O175.3
A
1008-5513(2012)02-0232-06
2011-11-16.
國家自然科學基金(10771165).
張婷婷(1985-),碩士生,研究方向:微分算子的譜與逆譜理論.
2010 MSC:34A 55,34L24

