IRT測驗等值流程化操作思路的構建

黎光明 張敏強

由于測驗等值涉及一些復雜的統計計算，給人們進行等值操作帶來了較大困難，阻礙了當前國內等值技術的發展。造成這種窘境，皆因等值操作困難化。如何使用方便的等值軟件進行思路清晰的流程化等值操作，是解決這一問題的關鍵所在。

1 測驗等值的概念

在教育與心理測量實踐中，經常遇到一個測驗需要配備多個測驗形式的情況，特別是那些測驗內容容易受記憶和針對性訓練影響的測驗，在測驗前需要嚴格保密，測驗后不能再用，必須配備多個不同形式供不同次施測使用。然而，各個不同形式的測驗測出的結果可能會有所不同。為了保證測驗的公平性和可比性，需要把不同測驗形式的分數都轉換到同一個分數系統上。測量學上把為達到這一目的而發展起來的一套專門技術稱為測驗等值（Test Equating）[1]。測驗等值是教育與心理測量中的一個重要研究領域。在我國考試實踐中有許多大規模的考試需要進行測驗等值[2]。進行測驗等值不是無條件的分數轉換，需要滿足同質性、等信度性、公平性、不變性等條件[3]。

基于不同的測量學理論框架，測驗等值可分為經典測驗理論（Classical Test Theory,CTT）測驗等值與項目反應理論（Item Response Theory,IRT）測驗等值兩種[4]。

2 IRT測驗等值的優勢

經典測驗理論的測驗等值方法存在不少困難與局限：首先，它們確定的轉換關系依賴于樣本，會隨被試樣組的不同而變化，等值條件的唯一性（不變性）要求不能滿足，無論哪種方法，都難以確保求出的轉換關系是對稱的、公平的。其次，經典測驗等值方法應用重點又都在被試觀察分數等值上，很難妥善解決難度、區分度這類項目參數等值的問題。最后，更重要的是，即使在線性等值的情況下，經典等值理論所認定的應予等值的測驗分數間的線性轉換關系，也是假設能夠存在的，而不是必然能夠具有的[3]。

項目反應理論卻根本不同，在所選反應模型與實測資料適合良好的情況下，按項目反應理論方法所確定的被試特質與項目參數間的轉換關系，就是必然應該具有的，這是因為特質與項目參數本應具有不變性。也正由于轉換關系是來自模型的理論性質本身，所以，能夠保證全面地較好滿足唯一性、公平性、對稱性等要求。另外，由于項目反應理論能同時估出特質與項目參數，特別是，項目難度又是直接定義在特質參數量綱上，因而，就能同時解決特質水平與項目參數的等值問題[5]。所以，項目反應理論等值不僅在理論上具有優良的性質，而且在實用上具有極強的功能。項目參數等值問題的解決為大型題庫的建設提供了有力的技術保證[6]。

3 IRT測驗等值流程化操作思路

在參考國內外關于測驗等值的相關文獻[7][8][9]的基礎上，構建出IRT測驗等值的流程化操作思路，如圖1所示。從圖1可以看出，進行IRT測驗等值，需要進行等值設計、數據收集、參數估計、量表化及測驗等值5個步驟。

3.1 等值設計

根據等值中介因素的不同，可以將測驗等值設計主要分成以下三種形式：

（1）單組設計。單組設計是指把應予等值的兩個或多個測驗同時向同一被試組施測，然后借助于同一被試組把應予等值的測驗聯系起來的等值設計。運用單組設計比較兩組測驗分數的差異主要歸因于兩個測驗的難度的不同。運用單組設計進行等值的優點是等值簡單且無抽樣誤差，缺點是存在練習效應、疲勞及厭倦等因素的影響，會給等值結果帶來偏差不明顯的誤差。

（2）等組設計。等組設計是指從同一總體中隨機抽取兩組考生，這兩組考生被認為在能力分布上是相同的或很接近，讓這兩組考生分別接受兩份不同測驗X和Y，然后把所得測驗分數加以等值的設計。這種設計方案可克服練習效應和疲勞等因素的不利影響，但由于兩組考生的能力分布可能不一樣，從而給等值帶來偏差。

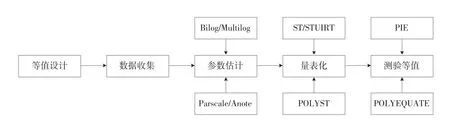
圖1 心理與教育測量IRT測驗等值的流程化操作及相應軟件

（3）錨測驗設計。錨測驗設計是指把應予等值的測驗分別向不同的考生組施測，并將“錨測驗”作為等值的測驗的“橋梁”所進行等值的設計。這種設計不要求兩個被試樣組的能力分布完全一樣，也不會給考生帶來太大的練習效應和疲勞因素，因此它兼有第一和第二兩種設計方案的長處，又克服了其短處。因此，在等值設計中，錨測驗設計是常被采用的一種[10]。

3.2 數據收集

當選定了相應的等值設計之后，一個重要的問題就是如何能準確有效地收集數據，以客觀而全面地反映所要研究的心理行為問題的真實狀況。數據收集需要注意二個方面：一是所收集的數據需要滿足等值設計的要求；二是數據必須有代表性，樣本容量不能過小。

多種等值數據資料的收集方法可以分為二大類，一類是采用以“人”為媒介的共同組設計，即讓一組人接受不同的測驗版本；另一類是以“題目”為媒介的“錨測驗”設計，即在不同測驗版本中含有共同的題目。共同組設計（common-subject equating design）中包括單組設計（single-group design）、平衡隨機組設計（counterbalanced random-group design）和等組設計（equivalent-group design）等幾種不同的設計。共同題等值設計（common-item equating design）包括錨測驗隨機組設計（anchor-test-random-group design）、錨測驗非等組設計（anchortest-nonequivalent-group design）、部分預先等值設計（section pre-equating design）、題目預先等值設計（item pre-equating design）等幾種不同的設計[7]。

3.3 參數估計

心理測量的目的往往是定量地表示人員的某處心理特質。比較直觀的方法就是根據被試答對項目的數目來進行這種定量描述。項目反應理論把被試潛在特質和項目參數放在同一個數學表達式中加以考慮。這種表達式就是項目反應模型，有時也稱為項目反應函數。測量工作者的任務就是要把項目反應模型中的各種參數（包括人員的潛在特質參數和項目參數）估計出來，估計這些參數受到諸多方面因素的影響，如題量及被試量等[11]。

在實際的測驗工作中，我們所能得到的只是被試對測驗項目答對或答錯的一組反應數據，并沒有任何一個項目參數的真實值。因此，必須根據觀察分數來對項目參數進行估計。項目參數估計的過程是項目反應理論中最困難、最重要的過程。由于它的高度復雜性，使得只有運用專門的計算機軟件才能很好地完成這一任務。

3.4 量表化

量表化是將兩個或多個考試放到一個統一量表上的過程。現代標準化測驗誕生的一個標志性測驗是法國心理學家比內（Binet）1905年出版的《比內智力測驗》。在這個測驗中,實際上已經包含了“量表化”的過程。這個測驗適用于不同年齡的兒童，對不同年齡的兒童施測的題目不同，所報告的是具有可比性的智力分數。在這個測驗中,已經包含了對不同“試卷”的量表化連接。在這一新的關于量表化的框架體系內，量表化過程被劃分為“構念（construct）相同”與“構念不同”兩種情況。

相當長的時間中，教育測量學家將等值分為橫向等值（horizontal equating）和縱向等值（vertical equating）。在考試的平行版本之間建立聯系的過程,被稱為橫向等值。有的時候,測驗被用來建立發展量表，一組水平不同的測驗被用來描述考生的發展水平。在這些不同水平的測驗之間建立聯系的過程被稱為縱向等值。顯然，這些被用于建立發展量表的測驗并不是相同水平的，將之稱為“等值”是不妥的[7]。將測驗之間的這類連接稱為“量表化”，似乎更為合理些。

3.5 測驗等值

測驗等值是教育與心理測量中的一個重要問題，同時又是測量實踐中的一個重要技術問題。從本質上說，測驗等值是通過對考核同一種心理品質的多個測驗形式作出測量單位系統的轉換，使所有測驗形式的測驗分數轉化到一個作為基準的度量系統上，進而使得這些不同測驗形式的測驗分數之間具備了可比性。等值是對同一個考試的不同版本的分數進行連接的過程，是在構念相同、難度相同、信度相同和考生目標總體相同的情況下的分數連接。與預測和量表化相比，等值的條件最嚴格，是兩個測驗分數之間最緊密的連接方式[7]。對考試分數進行等值處理不僅是保證測驗信度和公平性的重要環節，也是建立題庫和實現計算機化自適應性考試的核心環節。測驗等值是否可靠，可以通過考察產生的等值誤差來反映[12]。

目前，國內關于測驗等值方面的研究存在以下問題：一是國內一些教材測驗等值公式不統一，缺乏更新，甚至有明顯的符號遺漏；二是缺乏專門的數理統計推導，僅為介紹性地闡述，具體如何計算不得而知；三是未交待如何獲取可操作的等值軟件，造成一些初學者產生畏懼的心理。因此，使用方便的等值軟件進行思路清晰的流程化等值操作，顯得十分有必要。

4 IRT測驗等值流程化操作軟件

4.1 參數估計軟件

對于參數估計，項目反應理論包含一組分析軟件 包:BILOG、MULTILOG、PARSCALE、ANOTE等。這些軟件作為題目分析、題庫建設以及分數估計等方面的重要工具在各個領域被廣泛應用。

國際測量學界有幾個項目反應理論處理多級計分資料的分析程序，最著名和最流行的是MULTILOG和PARSCALE。它們既能處理社會心理測量與心理衛生評估中的5點、7點乃至更多級別的測評量表資料，又能處理成就測驗中的多等級計分題資料。但MULTILOG的最高等級數為10（即9個難度級別），PARSCALE的最高等級數為15（即14個難度級別）。在我國，心理測量等級計分資料一般多在9點以下，而成就測驗中，卻歷來有堅持綜合運用選擇題與多等計分題的良好傳統。一般，選擇題占分比重只是40%左右，主要部分是多計分題（即所謂的“主觀題”）；而且，不少題型（如作文、分析論述、綜合證明等）的滿分值常在15分乃至20分或30分以上。因此MULTILOG和PARSCALE在我國教育測量中的使用范圍就受到一定限制。為滿足我國教育與心理測量工作實際發展的需要，近年來江西師范大學漆書青和戴海崎等人開發編制了通用測量程序（Analysis of Test System，ANOTE）。它能處理難度級別數超過20的等級計分資料。

4.2 量表化軟件

（1）ST。ST是一個用于計算項目反應理論量表轉換函數的C語言程序，適用于三參數邏輯斯蒂克模型（three-parameter logistic model,3PL,其中 D=1.7），適用于錨測驗設計（共同項目）。量表轉換方法：Haebara（1980）和Stocking-Lord（1983）。程序發布日期：2004年5月24日，版本：Windows Console Version。可登錄 http://www.uiowa.edu/～casma 進行免費下載。

（2）POLYST。POLYST是一個用于計算項目反應理論量表轉換方法的ANSI C程序，適用于參數邏輯斯蒂克模型（Logistic mode）、等級反應模型（Graded Response model,GR）、拓廣分部評分模型（Generalized Partial Credit model,GPCM）、稱名模型（Nominal Response model，NR）和用于多重選擇項目的模型（Multiple-choice model,MC），適用于等組或單組設計（共同被試）。量表轉換方法包括mean/sigma（Marco,1977）、mean/mean（Loyd&Hoove,1980）、haebara（Haebara,1980）和 Stocking-Lord（Stocking&Lord，1983）。程序發布日期：2003年5月12日，版本：Version 1.0。可登錄http://www.uiowa.edu/～casma進行免費下載。

（3）STUIRT。STUIRT是一個用于計算項目反應理論量表轉換的程序，適用于參數邏輯斯蒂克模型、等級反應模型、拓廣分部評分模型、稱名模型和用于多重選擇項目的模型，適用于錨測驗設計（共同項目）。量表轉換方法包括mean/sigma（Marco,1977）、mean/mean（Loyd&Hoove,1980）、haebara（Haebara,1980）和 Stocking-Lord（Stocking&Lord，1983）。STUIRT可看作是POLYST的擴展版。ST和POLYST僅能處理單一格式的測驗（Single-format test form），也就是數據形式要么是二值，要么是多值。但是，STUIRT既可以處理二值數據，也可以處理多值數據，這類測驗叫做混合格式測驗（mixed-format test）。STUIRT是依靠共同項目（common item）來進行量表化的，因此它是測驗等值良好量表化軟件，特別適用于后面要介紹的POLYEQUATE軟件（簡直就是為它設計的）。程序發布日期：2004年9月，版本：Version 1.0。可登錄http://www.uiowa.edu/～casma進行免費下載。

4.3 測驗等值軟件

（1）PIE。PIE（program for IRT Equating）是在Windows平臺下進行IRT測驗等值的程序。它既能處理IRT觀察分數測驗等值，也能處理IRT真分數測驗等值。PIE僅適合IRT的基本模型，即邏輯斯蒂克模型，且D=1.7。在ST對收集到的數據進行量表化之后，方可使用PIE程序。程序發布日期：2004年5月20日，版本：Windows Console Version。可登錄http://www.uiowa.edu/～casma進行免費下載。

（2）POLYEQUATE。POLYEQUATE是一個由Fortran語句編寫的程序，既可以處理IRT觀察分數等值，也可以處理IRT真分數等值。與PIE相比，它可以處理多值的項目反應理論模型，如三參數邏輯斯蒂克模型（Three-parameter Logistic Model）、塞姆吉馬正態肩形等級反應模型（Samejima’s normal ogive Graded Response model）（Samejima,1997）、塞姆吉馬邏輯斯蒂克等級反應模型（Samejima’s Logistic Graded Response model）（Samejima,1997）、貝克的稱名模型（Bock’s nominal model）（Bock,1997）和馬如克的拓廣分部評分模型（Muraki’s Generalized Partial Credit model）等。程序發布日期：2004年7月7日，版本：Windows Console Version。可登錄http://www.uiowa.edu/～casma進行免費下載。

5 IRT測驗等值流程化操作實際例舉

5.1 等值設計

2005年佛山市普教進行課程改革，分為“課改實驗區”和“非課改實驗區”[13][14]。課改區與非課改區考生能力有所差異，且測驗X與Y中有一個共用錨測驗，采用非等組錨測驗設計作為本研究的等值設計。IRT等值方法主要有MM（mean/mean）、MS（mean/sigma）、HA（Haebara）和SL（Stocking-Lord）方法。Stocking-Lord是基于項目特征曲線等值方法，具有較多優良特性，本研究統一選用此種方法來進行測驗等值。

5.2 數據收集

由廣東省佛山市教育局提供的2005年“中考數學”實測數據。“中考數學”相應分為課改區的測驗X和非課改區的測驗Y。課改區有考生50 902人，非課改區有考生10 882人。測驗X、測驗Y各有24道題，其中客觀題15道，主觀題9道。測驗X和測驗Y有一個錨測驗V，測驗V的主客觀題共9道。

5.3 參數估計

依據各種等值模型分別對測驗X和測驗Y進行參數估計，得出各測驗的項目參數值。使用的軟件是 Parscale 3.5[15]和 Multilog 7.0[16]，其中 Parscale用于估計SL、SN和GPCM的參數，Multilog軟件用于估計NR的參數。X（50902）和Y（10882）的數據參數估計結果格式如表1所示。

在表1中，NR表示稱名反應模型，GR表示等級反應模型，PC表示分部評分模型，DW表示缺省權重，1.0/1.7表示模型的系數，aX和aY分別表示X測驗和Y測驗估計的各題區分度，bX和bY分別表示X測驗和Y測驗估計的各題難度。

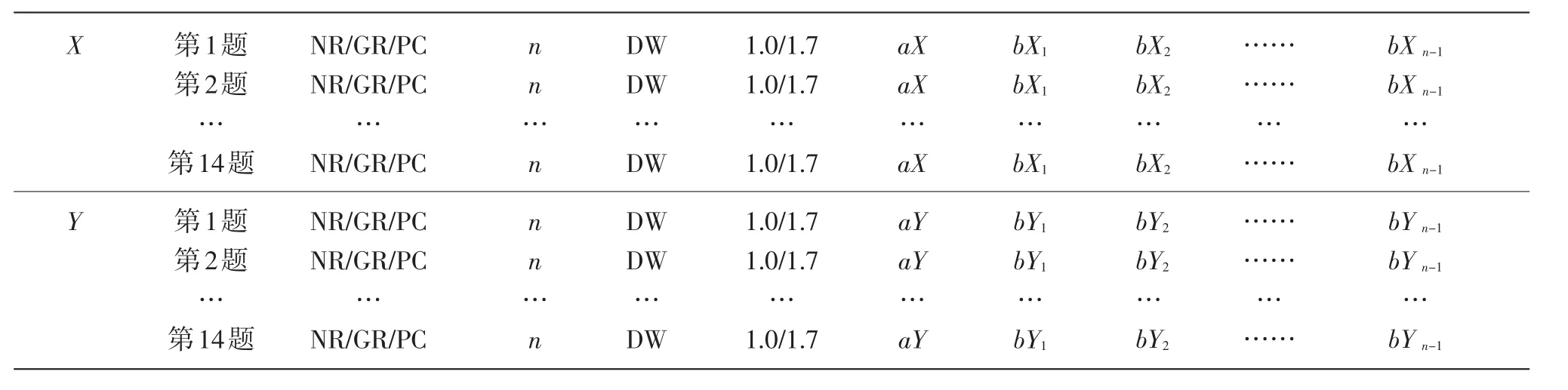
表1 等值測驗X和Y數據參數估計結果格式

5.4 量表化

根據等值測驗X（50902）和Y（10882）數據參數估計結果，將測驗X和測驗Y所得兩測驗的項目參數進行量表化（Scaling），即統一量綱，使用的是STUIRT軟件。Multilog的稱名反應模型的量表化格式、Parscale的SL和SN模型的量表化格式、Parscale的PCM模型的量表化格式分別如圖2～圖4所示。

根據圖2～圖4的量表化格式，編寫相應的程序，等值測驗X（50902）和Y（10882）數據的量表化結果格式如圖5所示。

圖2 NR量表化格式

圖3 GR量表化格式

圖4 PCM量表化格式

5.5 測驗等值

根據測驗X和測驗Y量表化的結果，通過POLYEQUATE軟件進行等值轉換，其程序如圖6和圖7所示。

圖6 POLYEQUATE等值程序

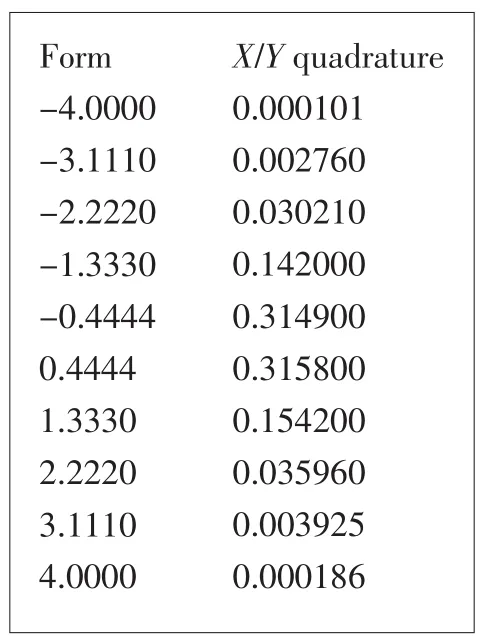
圖7 POLYEQUATE等值程序中qform代碼

測驗等值進行后，將得到四種IRT模型下的測驗觀察分數等值結果。四種IRT模型下的測驗觀察分數等值部分結果列于表2。為節省篇幅，以10分為一分數段列出。

表2 四種IRT多級模型測驗觀察分數等值結果(舉例)

在表2中，X表示課改實驗區原始分數，f表示頻數，Y（）表示SL、SN、PCM和NR方法將X原始分數等值到Y測驗上的原始分數是。通過表2可以將實驗區與非實驗區分數進行相互轉換，從而達到測驗等值的目的。

6 結語

在我國，測驗等值是測驗研究中相對薄弱的一個環節，許多重要的考試都尚未實現統計等值。嚴格按照上述規定進行測驗等值操作，能夠得到理想的等值結果。這種規定式的等值流程化操作思路，有助于“手把手”教人們如何進行測驗等值，從而能夠克服進行等值時產生的畏懼心理，即便是“生手”，在看清等值操作的流程圖后，也可能覺得操作起來相對簡單。等值流程化操作有助于解決測驗等值操作困難化的難題，使得許多初學者有一個感性的認識，并以此為基礎繼續深入探討一些具體的等值問題。按照心理與教育測量IRT測驗等值流程化操作思路，將有利于促進人們積極參與等值化操作，從而推動我國測驗技術的發展。

[1] 戴海崎,張鋒,陳雪楓.心理與教育測量(第三版)[M].廣州:暨南大學出版社.2011.

[2] 張敏強.教育測量學[M].北京:人民教育出版社.1998.

[3] 漆書青,戴海崎,丁樹良.現代教育與心理測量學原理[M].北京:高等教育出版社.2002.

[4] 張敏強,黎光明,劉曉瑜,焦璨.教學管理與評價的測量技術:測驗等值的理論、方法及應用.教育研究與實驗[J],2009,2：54-57.

[5] Von Davier,Alina,A.L.,&Wilson,C.Investigating the population sensitivity assumption of item response theory true-score equating across two subgroups of examinees and two test formats.Applied Psychological Measurement,2008,32(1)：11-26.

[6] 周駿,歐東明,徐淑媛,戴海崎,漆書青.等級反應模型下項目特征曲線等值法在大型考試中的應用[J].心理學報,2005(6):832-838.

[7] 謝小慶考試分數等值的新框架考試研究[J].考試研究,2008,4(2):4-17.

[8] Kolen,M.J.,&Brennan,R.L.Test Equating:Methods andPractices.Springer-Verlag New York Inc.1995.

[9] Kolen,M.J.,&Brennan,R.L..Test equating,linking,and scaling:Methods and practices(2nd ed.).New York:Springer-Verlag.2004.

[10] 黎光明,劉曉瑜,張敏強.測驗等值技術在中小學教學管理與評價中的應用[J].教育測量與評價(理論版),2009,14(3):8-11.

[11] “基礎教育教學質量監測系統”項目組(張敏強,黃憲,焦璨,黎光明等).IRT下題量與被試量對參數估計模擬返真性能的影響.中國考試,2009(6):3-10.

[12] 黎光明,張敏強.全測驗與錨測驗題型分值比對等值誤差的影響.考試研究,20095(3):71-77.

[13] 張敏強,黎光明,焦璨.普教“升中”考試中測驗等值的應用研究——以廣東省佛山市“升中”考試為例.心理與行為研究,2009，7(1):27-31.

[14] 黎光明,張敏強.IRT測驗等值模型的選擇——以廣東佛山市中考數學實測數據為例.中國考試,2012,2:8-13.

[15] Thissen,D.Multilog user’s guide:Multiple,categorical item analysis and test scoring using item response theory[Computer program].Chicago:Scientific Software International.1991.

[16] Muraki,E.,&Bock,R.D.PARSCALE(Version 3.5):IRT item analysis and test scoring for rating-scale data[Computer program].Lincolnwood,IL:Scientific Software.1998.