一種改進的嵌入式零樹小波編碼方法

胡靜濤，陳 衛

( 陸軍軍官學院5 系，合肥 230031)

圖像數據壓縮就是通過減少圖像數據之間的冗余來減少數據量，從而達到減少存儲空間，提高傳輸效率的目的［1］。上個世紀90年代后，圖像壓縮編碼研究取得了一系列的階段性新成果，基于零樹的編碼法首先由A.S.Lewis 和G.Knowles 提出［2］，其特點是根據小波系數在同方向子帶中的相似性，利用一種稱為小波樹的樹形結構來組織小波系數，使其能去除頻域和空間域中的相關性［3］。接著Shapiro 結合比特平面編碼方法設計了一種更好的零樹編碼方法—嵌入式零樹小波編碼( EZW)方法［4］，Shaprio 提出的嵌入式零樹小波算法，它有效地利用了小波系數的特性，實現了圖像的可分級編碼。但也存在算法時間長和空間復雜度過高的缺點。

1 嵌入式零樹小波編碼

1.1 嵌入式編碼

嵌入式編碼即編碼器把待編碼的比特流按照重要性的不同進行排序，根據目標碼率要求隨時結束編碼;對于給定的碼流，解碼器也能夠在任意點結束解碼，并可以得到相應目標碼率的解碼圖像。從均方誤差的角度看，幅值較大的系數所包含的信息量相對較大，一旦丟失引起的失真度也較大。為了減少失真度，在處理過程中優先編碼和傳輸幅值較大的系數［5］。

嵌入式編碼即將變換系數按照幅值從大到小排列，首先傳輸幅值最大的變換系數的位信息，也就是最重要的信息，然后傳輸次重要系數，最后傳輸的系數最不重要［6］。在傳輸前所有的變換系數用二進制的方式表示，如圖1。

1.2 零樹小波編碼

1.2.1 小波樹結構

小波分解后，各個分辨率子帶中的系數并不是完全獨立的，圖像的子帶之間有結構的自相似性，具有結構冗余［7］。各分辨率子帶系數間有如下的對應關系［8］。

1)除了最高分辨率的子帶外，每一個小波系數都與同空間方向的高一級分辨率等級內的一組小波系數相聯系;

2)系數之間比較，處于低分辨率等級子帶的系數稱為父系數，在同一方向高一分辨率等級，并且與其在相同空間位置的所有系數稱為它的子系數;

3)對于一個給定的父系數，與其在同空間方向，且分辨率等級更高的所有子系數，稱為它的子孫系數;

4)除了最低分辨率的子帶，所有的父系數都有4 個子系。

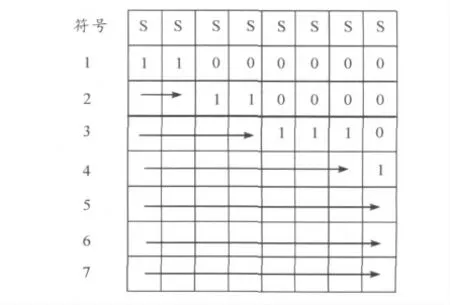
圖1 按幅度排序信息的二進制表示

圖2 為一個采用上述方式進行三級分解的小波樹。其中箭頭方向表示，由父系數子帶指向子系數子帶［9］。

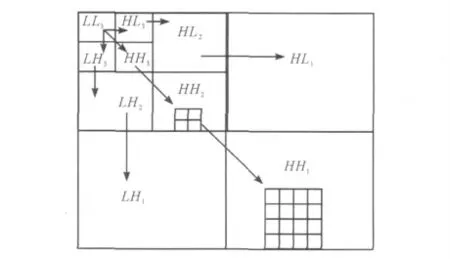
圖2 子帶間的父子關系

在對小波系數編碼時，對小波系數的掃描應保證沒有子孫系數在其父系數之前被掃描。對一個N 級分解小波變換，掃描從最低頻子帶LLN開始，然后掃描HLN，LHN，HHN，再掃描下一分辨率等級的子帶HLN-1，LHN-1，HHN-1，如此繼續，最后掃描HH1。如圖3 所示。

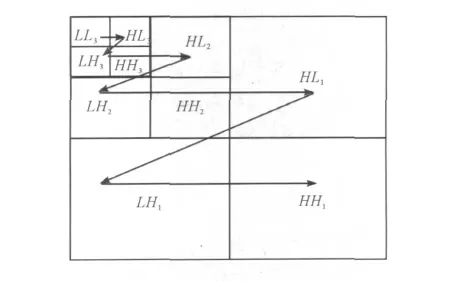
圖3 小波系數掃描順序示意圖

要想在解碼端恢復出原圖像，需要傳送小波系數的排序信息和位信息。如果每個小波系數的排序信息和位信息都要傳送的話，這樣需要的數據花銷是非常大的，根本就達不到壓縮的目的，但是零樹結構的存在解決了這個難題［10］。

零樹的數據結構:對于一個小波系數xi，如果對于一個給定的門限T，＞T，則稱該小波系數為重要系數，否則為不重要系數［25］。正重要系數用符號POS( positive)表示，負重要系數用符號NEG( negative)表示。如果該系數為不重要系數，但是其子孫系數中有重要系數，則該系數為孤立零點，用IZ( isolated)表示。如果該系數為不重要系數，但是其子孫系數中沒有重要系數，且該系數的父系數為重要系數，則該系數為零樹根，用ZTR( zerotree)表示，該系數和其子孫系數就形成了一個零樹，在低分辨率上的那個小波系數被稱為母體，是樹根;在高分辨率上同方向相應位置上的那些小波系數稱為孩子。通過這種零樹結構，巧妙地編碼，使用于描述重要系數的位置信息大大減少。

1.2.2 逐次逼近量化

在EZW 算法中使用的是逐次逼近量化( successive approximation quantization，SAQ)方法。逐次逼近量化的主要思想是，通過逐次使用閾值序列T0，T1，…，TN-1來判斷小波系數的重要性，并確定其類型碼和幅值碼［11］。

在整個編( 解)碼過程中，始終存在著兩個過程—主掃描和輔掃描，它們交替進行，逐次提高量化精度。主掃描對應一張不斷更新的主表，輔掃描對應一張不斷更新的副表。通過這兩個過程對重要系數、零樹根和孤立零點構成的重要圖進行編碼，。實質上是對重要系數的位置和幅值編碼。

2 EZW 算法的不足

雖然EZW 算法存在許多優點，算法簡單，編碼效率高。但是也存在著一些不足，主要表現在以下幾個方面［5］:

1)在編碼的過程中要形成許多棵零樹，每生成一棵零樹需要對數據掃描兩遍，而且每一棵零樹必須要在前一棵零樹生成之后才能生成，造成編碼效率低。對于一個小于閾值T的小波系數，為了判斷其是孤立零還是零樹根，必須對其所有后代系數進行掃描，勢必增加編碼時間，導致編碼速度較慢。

2)通過前面的分析我們知道，經過小波變換后的系數重要程度不同。低頻系數重要，而高頻系數相對不重要。但是EZW 對所有頻域不加區分，進行同等重要程度的編碼，沒有充分利用小波變換后系數的特點。。

3)在EZW 算法中樹間存在大量的冗余，但是EZW 算法沒有利用樹與樹之間的關系來減小樹間冗余。

4)同一子帶中相鄰系數之間有一定的相關性，在高頻系數中表現的尤為突出，通過子帶的集合可以進一步地壓縮數據。但是EZW 算法并沒有對這種相關性進行充分的利用。

3 EZW 算法的改進

3.1 頻率優先性

根據小波變換的理論可知，一幅圖像經過小波變換后雖然其數據和總能量沒有減少，但是其能量分布產生了比較大的變化。在低頻系數子帶中聚集了原始圖像的大部分能量，高頻系數只占有圖像的一小部分能量。本文中的改進算法是把高頻子帶系數和低頻子帶系數分開處理。針對低頻子帶系數，單獨對其進行無失真編碼，采用差分脈沖編碼調制( DPCM)，對編碼后的碼流再進行熵編碼，進一步壓縮碼流，提高壓縮效率。

DPCM 預測編碼的系統原理框圖［12］，如圖4。

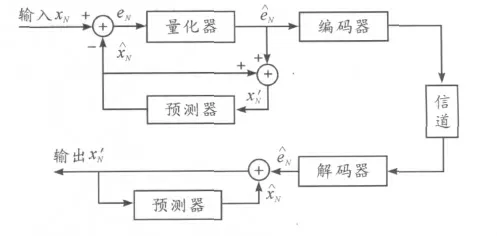
圖4 DPCM 原理圖

3.2 重要子帶編碼［13］

在原始嵌入式零樹編碼中，為了找到重要系數和確定零樹根的位置，為了確定一個小波系數是零樹根還是孤立零，往往需要掃描整棵四叉樹和大量重復的掃描，時間復雜度高，同時消耗了大量的內存。

如果在掃描中事先就能確定重要系數可能存在的位置，只對重要系數存在的子帶進行掃描，對不存在重要系數的子帶不掃描，這樣將在一定程度上減少掃描時間，提高壓縮速度。由小波變換原理我們可以知道，一幅圖像經過N 級小波變換分解后，形成了3N+1 個子帶。首先，尋找每個子帶中的小波系數的最大值。即IK(1，2，3，…，3N+1)中小波系數的絕對值的最大值tK，其中1 ＜k ＜3N+1。圖5 給出3 級圖像小波分解后的每個子帶系數絕對值的最大值的示意圖。

第一次掃描時確定初始閾值T0，其確定方法與原始EZW方法相同。對于每一個子帶將其絕對值最大值tK與T0進行比較，若tK＞T0，則該子帶稱為重要子帶;若tK＜T0，則該子帶稱為不重要子帶。開始掃描時，仍然按照morton 掃描順序進行掃描。在整個編碼中用p 表示正重要系數，n 表示負重要系數，t 表示不重要系數，i 表示非重要子帶。當掃描時發現tK＜Ti時，用i 來表示這個不重要子帶，同時不用再掃描該子帶，直接掃描下一個子帶;當tK＞T0時，用p 表示正重要系數，n表示負重要系數，t 表示不重要系數，i 表示非重要子帶。

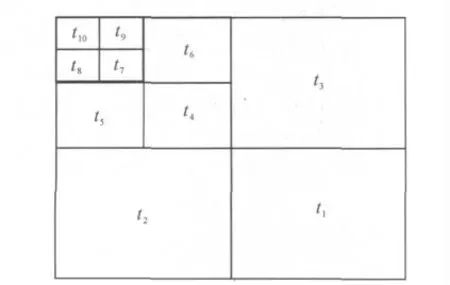
圖5 子帶系數最大值示意圖

3.3 熵編碼

對高頻系數編碼后形成的碼流進行熵編碼，減少數據量，本文采用霍夫曼編碼。

綜上所述，整個改進算法的流程如圖6。

圖6 改進算法的流程

4 實驗仿真

為了更直觀地說明算法的有效性，本文對改進算法進行實驗仿真。

實驗環境:Windows XP 系統，內存1G，Matlab7.0。

測試圖像為Matlab7.0 中的測試圖像westconcordorthophoto。

對圖像采用db9/7 小波基對圖像進行3 級分解與重構。

圖7 測試圖像westconcordorthophoto

仿真圖片對比∶壓縮比20∶1。

從上面得到的實驗圖像表明:

1)改進后的EZW 算法重構圖像的質量較高，主觀視覺效果較好，不產生任何方塊效應;

2)在低碼率時，改進算法的重構圖像質量優于原EZW算法。

［1］劉峰.視頻圖像編碼技術及國際標準［M］.北京:北京郵電大學出版社，2005.

［2］Lewis A S，Knowles G. Image compression using 2 - D wavelet transform［J］. IEEE Trans. On Image Processing，1992，1(2):244-250.

［3］王文波.基于小波的圖像壓縮編碼［D］.成都:電子科技大學，2009.

［4］Shapiro J M. Embedded image coding using zerotrees of wavelet coefficients［J］. IEEE Trans.On Signal Processing，1993，41(12):3445-3462.

［5］成禮智，王紅霞，羅永.小波的理論與應用［M］.北京:科學出版社，2004.

［6］王向陽等.基于自適應小波變換的嵌入式圖像壓縮算法［J］.微電子學與計算機，2005，22(2):121-123.

［7］李亮.基于小波變換的靜態圖像壓縮編碼研究［D］.大連:大連交通大學，2009.

［8］張春田，蘇育挺，張靜.數字圖像壓縮編碼［M］.北京:清華大學出版社，2006.

［9］劉學鋒.基于小波零樹的嵌入式圖像編碼技術的研究與改進［D］.西安:西安科技大學，2006.

［10］薛冰. 嵌入式零樹小波編碼算法的改進與應用研究［D］.成都:電子科技大學，2008.

［11］陳冬，張田文，李東.位漸進逼近量化的EZW 改進算法［J］.哈爾濱工業大學學報，2010，42(5):779-783.

［12］姚敏，趙敏.改進的高效EZW 遙感圖像壓縮方法研究［J］.電子科技大學學報，2009，38(4):525-528.

［13］雷梅梅，余諒. 一種改進的嵌入式小波圖像編碼算法［J］.計算機工程與科學，2010，32(10):59-62.