基于粗糙集與覆蓋算法的概率模型的通信信號分類方法

林 偉

(陸軍軍官學院，合肥 230031)

通信信號的識別與分類關系密切，信號分類是信號識別的基礎。然而，現代電磁環境日趨復雜，新的通信體制通信信號不斷涌現，信號分類和識別難度越來越大。“分類問題”已成為人工智能中的一個重要研究方向。如何根據現代通信信號的特點，選擇合適的分類方法識別通信信號已經成為一個迫切需要解決的難題。

關于分類問題，國內外許多專家都進行了廣泛、深入的研究，并取得了一些可喜的成果，如貝葉斯分類、決策樹分類法等。但是，貝葉斯分類必須已知先驗概率和類別個數，不便用于通信信號分類［1］;由于通信信號存在不便量化的非數值型特征參數，有時不便進行神經計算，神經網絡分類方法有時受到限制［2］;支持向量機是目前分類效率較高的方法，但算法復雜度相應提高，對非數值型數據處理也不合適［3］;決策樹的訓練耗費很大，運算復雜度太高［4］。所以，用以上一種單純分類方法對通信信號分類不能最優。

根據通信信號特征參數的特點，給出了一種將粗糙集理論與覆蓋算法的概率模型結合起來的模式分類方法，這種方法實際上是將粗糙集和覆蓋算法的概率模型相結合的兩級復合分類方法。第1 級分類利用粗糙集進行粗分，該理論在屬性約簡、消除冗余信息等方面有優勢，能針對特征參數中非數值型參數簡化信號屬性，提取其核心屬性，針對核心屬性，根據分類目的進行粗分;第2 級分類借助覆蓋算法概率模型細分，用覆蓋算法構造神經網絡，引入高斯有限混合模型，對數值型特征參數，具有良好的分類性能，能實現精確分類，對粗分后的子集進行精確分類。

1 粗糙集與覆蓋算法概率模型相結合的分類方法的實現

粗糙集理論與覆蓋算法在模式分類中各有優勢。粗糙集方法能簡化規則，消除冗余信息;覆蓋算法的概率模型能提高分類精度。在解決實際問題時，可以根據決策屬性選擇解決方法。設決策屬性為D，條件屬性C =C1∪C2，其中C1是非數值型條件屬性，C2是數值型條件屬性，有3 種方法供選擇:

方法1 若D=f(C1)，即D 只由C1決定，可用粗糙集方法;

方法2 若D=f(C2)，即D 由C2唯一決定，可用覆蓋算法的概率模型;

方法3 若D=f(C1∪C2)，即D 由C1和C2共同決定，則采用二者相結合的方法。

例如，一信息表是一個班的學生基本情況表，若D =性別，則用方法1;若D=全體學生平均成績，則用方法2;若D=男女學生的平均成績，則用方法3。

方法3 具體實現步驟:

1)基于粗糙集的非數值型條件屬性約簡:

①求出決策屬性D 的非數值型條件屬性C 的正區域POSC(D);

②對每一個非數值型條件屬性ci，計算POSC-{ci}(D)，若POSC-{ci}(D)=POSC(D)，則ci是可約去的，否則，ci不可約去，從而得非數值型條件屬性的核CORE(C);

③求含CORE(C)的最小集合P，使得POSP(D)=POSC(D)，得C 的最小約簡P。

2)將輸入空間的學習樣本約簡為只含core［］中核值屬性的樣本，得簡化的學習樣本。

3)對數據粗分類，根據需求篩選出滿足非數值型條件屬性的子集。

4)基于覆蓋算法的概率模型的海量數據挖掘算法的分類。

給定m 類分類的訓練樣本集K={K1，K2，…，Km}，算法實現具體步驟:

①利用覆蓋算法，求出各類的覆蓋組{C1，C2，…，Cm}:

a)將所有點投影到Sn上(中心在原點，半徑為R，R ＞

b)若K1(開始時i =1)非空，作一覆蓋m，j=1，2，…，gi，它只覆蓋K1的點，被Cij 覆蓋Ki的子集為Kij(j=1，2，…，gi);

c)若Ki被覆蓋完，i=i+1，若i ＞m，則轉至h，否則，任取Ki中尚未被覆蓋的一點ai;

e)求C(ai)所覆蓋點的重心，將其映射到球面上，設投影點為，按④中公式求，求得球形領域C);

g)求ai的平移點，并求對應的球形領域C)，若C)覆蓋的點數大于C(ai)所覆蓋的點數，轉到e)，否則，得到C(ai)的一個覆蓋，轉步c);

h)樣本學習結束，得到覆蓋組。

②以覆蓋的中心為高斯核函數的均值，取半徑為方差，對每覆蓋引入高斯核函數;立有限混合概率模型;

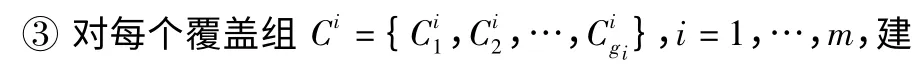
④利用文獻［5］中給出求解最大似然的迭代EM 算法進行最大似然擬合;

⑤訓練結束將得到p 個球形領域，所有訓練樣本被分成m 類不同覆蓋集合K={K1，K2，…，Km}，其中Ki=Ki1∪Ki2∪…∪Kij(i=1，2，…，m，p≥m)。

方法3 的步驟1 和2 降低了輸入數據的維數，步驟3 減少后續覆蓋算法的樣本個數，步驟4 具有較高的分辨能力，因此方法3 既快速又準確。

2 通信信號分類實驗

實驗用某型號接收機接收并采集通信信號，提取其特征參數，如表1 所示，信號U1、信號U2 和信號U3 的特征是從采集廣播電臺的數據中提取的，信號U4 和信號U5 是自己用某型號電臺發射信號，經接收和采集而提取的。表1、2 中，U為論域，即信號個體;Xi(i=1，2，…)為信號屬性，其中X1為調制樣式，X2為信號的頻率波段，X3為頻率(kHz)，X4為強度(信號歸一化功率)，X5為帶寬(kHz)，X6為調制參數，X7為信號應用領域;Y 為決策屬性，即結果。

C={X1，X2，…，Xn}為條件屬性集，∩(C -X7)=∩C，所以X7為C 中可省略的，同理約簡其他冗余屬性，得到約簡后的屬性集Score={X1，X2，…，X6}，如表2 所示。

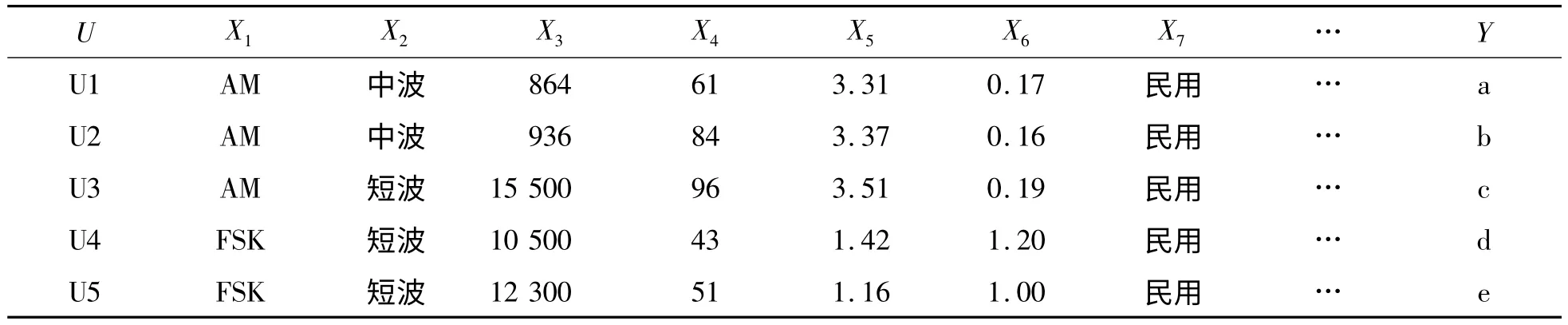
表1 通信信號的部分特征

表2 是完備屬性集，因為∩(C -{Xi})≠∩C，即Xi是不可省略的(i =1，2，…，6)。與表1 相比，信號的屬性個數減少了，即輸入數據維數降低了。因此，可以根據需求，利用非條件屬性進行粗分類。若需求為X1=“AM”，X2=“中波”，經過粗分類，只有信號U1 和信號U2 滿足要求，接著對這2 個信號用覆蓋算法概率模型細分，其他3 個信號就不再作細分的考慮。因此減少了進行覆蓋計算的樣本數，對大規模模式分類具有重要的意義。

實驗在不同時間分別大量接收并采集表1 中的所有信號，提取其特征向量，用方法1、方法2 和方法3 比較，結果如表3 所示。

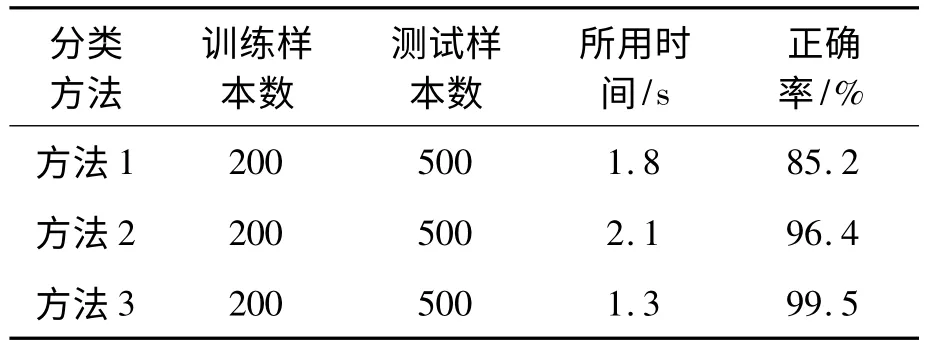
表3 通信信號分類與識別結果

通過表3，可以發現采用粗糙集和覆蓋算法覆蓋模型相結合的方法比單獨使用粗糙集或覆蓋算法概率模型，在所用時間和正確率上都有大幅度的提高，說明這種方法是有效的。

3 結束語

分類是識別的基礎，是人工智能研究的一個重要課題。關于分類問題，國內外許多專家都進行了廣泛、深入的研究，并取得了一些可喜的成果，但是，沒有一種分類方法對所有事物的分類都適用，沒有一種方法對任何分類問題都最優。本文分析了常用的分類方法的優缺點，根據通信信號的特點，提出了基于粗糙集和覆蓋算法的概率模型的通信信號分類方法。首先利用粗糙集能夠進行屬性約簡、消除冗余信息等方面有優勢，簡化特征參數中非數值型參數的信號屬性，提取其核心屬性;然后再借助覆蓋算法概率模型具有良好的分類性能，對數值型參數細分，對粗糙集約簡后的最小屬性子集進行分類。最后給出了算法的實現步驟，對實際信號進行了分類實驗，實驗效果證明提出的方法是適用的。

［1］Heckman D，Geiger D，Chickering D.Learning Bayesian networks:the combination of knowledge and statistical data.Machine Learning［J］.1995，20(3):197-243.

［2］張鈴，張鈸.人工神經網絡理論及應用［M］.杭州:浙江科學技術出版社，1997.

［3］崔偉東，周志華，李星.支持向量機研究［J］.計算機工程與應用，2001(1):58-61.

［4］Hunt E B，Marin J，Stone P T. Experiments in Induction［J］.Academic Press，1966，63:227-230.

［5］Dempster A P，Laird N M，Rubin D B.Maximum likelihood from incomplete data using the EM algorithm(with discussion)［J］.R Stat Soc Ser B，1977，39:1-38.

［6］陳敏. OPNET 網絡仿真［M］. 北京:清華大學出版社，2004.

［7］王文博，張金文.OPNET Modeler 與網絡仿真［M］.北京:人民郵電出版社，2003.

［8］劉建國，柯鈺，鐘京立.軍事通信網絡基礎教程［M］.北京:北京航空航天大學出版社，2001.

［9］張玉，楊曉靜.地域通信網網絡性能的計算機仿真研究［J］.計算機工程，2004(8):51-54.

［10］何非常.軍事通信［M］.北京:國防工業出版社，2000:24-75.

［11］岳偉甲，劉昌錦.一種基于VC ++的通信信號仿真軟件設計［J］.四川兵工學報，2011(5):92-95.