基于CAD技術的特征線中子輸運計算程序開發

陳珍平，王電喜，何 桃，王國忠，鄭華慶，FDS團隊

（1.中國科學技術大學，安徽 合肥 230027；2.中國科學院核能安全技術研究所，安徽 合肥230031）

中子輸運問題一直是核反應堆物理分析與輻射屏蔽設計研究的重點問題之一。隨著反應堆技術的快速發展，在未來進行先進反應堆設計與分析時對中子學模擬計算程序的要求也越來越高，主要體現在計算精度、計算效率以及處理幾何復雜度等方面，因此開發具有自主知識產權的、快速精確的中子學計算程序將具有非常重要的意義。特征線方法[1］（Method of Characteristics，MOC）是近年來在中子輸運計算與數值模擬研究中熱點研究的方法之一。該方法是從中子輸運方程的全微分形式出發，沿著中子飛行軌跡（稱為特征線）進行積分求解的一種確定論方法。由于該方法同時具有碰撞概率法和離散縱標法的優點，且理論上不受計算模型幾何形狀的限制，近十多年來已逐漸成為國際上求解中子輸運方程的主要確定論方法之一。

長期以來，阻礙特征線方法能否廣泛應用的主要問題在于能否將特征線理論與有效的幾何處理方法結合起來。本文在FDS團隊自主研發的大型集成多功能中子學計算與分析系統VisualBUS[2－3］框架下，利用核與輻射輸運計算自動建模軟件 MCAM[4－6］的幾何處理能力進行特征線方法幾何預處理，可高效、快速地完成幾何建模、網格剖分和特征線生成等幾何處理功能。最后，利用基準例題對特征線數值計算方法和程序進行了充分地檢驗，其結果驗證了本研究幾何處理方法和計算程序的正確性與可靠性。

1 特征線理論

特征線方法是將中子輸運方程沿著中子飛行軌跡和特定的離散方向進行輸運求解的一種方法。在本文中，對方位角離散采用Filippone[7］提出的離散方法；對極角離散耦合了LO離散和TY離散[8］方法；對幾何模型區域進行非結構網格剖分，劃分為許多平源近似區，在每個平源區里的中子源項被認為是常數。

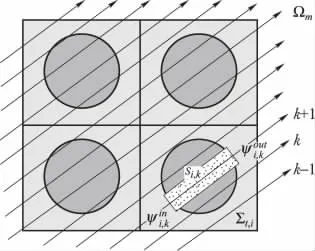
圖1 特征線示意圖Fig.1 The characteristic lines of MOC

根據前面的基本假設，單群特征線中子輸運方程可表示為：

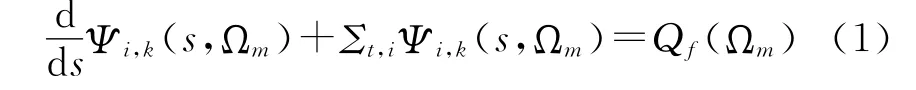
其中：

s是特征線長度，Σt，i是區域i的宏觀總截面，Ψi，k（s，Ωm）是區域i沿著特征線方向長度為s處的中子角通量密度，Qf（Ωm）是區域i的中子源項。

方程（1）為一階線性微分方程，可以解析求解得到：

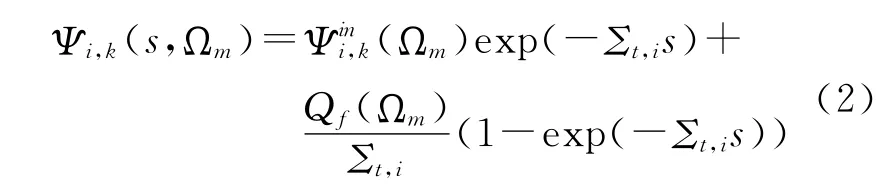
式（2）中Ψini，k（Ωm）是特征線k入射到區域i里入射點處的入射角通量密度。

根據方程（2）可以得到，特征線k穿出區域i的出射角通量密度為：

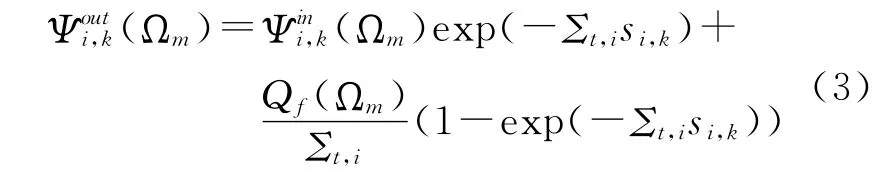
式（3）中si，k是特征線k穿過區域i的總長度；將特征線k上所有點的角通量密度進行積分平均，則可以獲得特征線k上任一點的平均角通量密度：

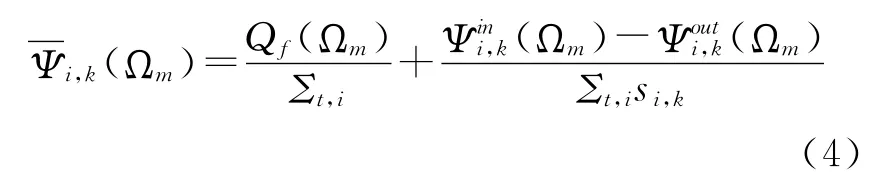
同理，將穿過區域i的所有特征線上的平均通量密度在i區進行體積加權平均，可獲得區域i的平均角通量密度：

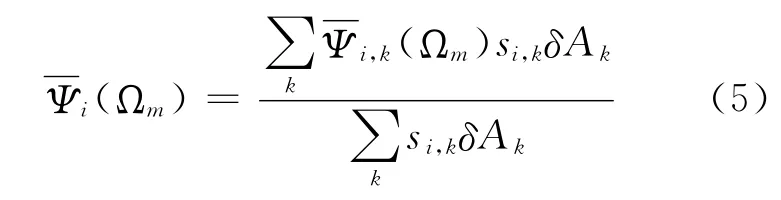
式中δAk為特征線間距。

將區域i各個離散方向的角通量密度進行加權求和，得到區域i的平均中子標通量密度：

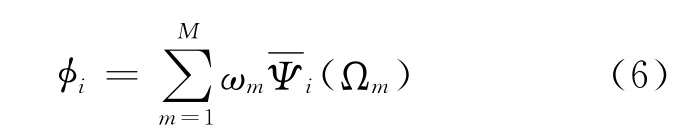
式中ωm是方向Ωm對應的離散權重，M為空間離散方向總數目。

2 幾何預處理方法

2.1 幾何建模

FDS團隊自主研發的核與輻射輸運計算自動建模軟件MCAM實現了多種商用工程CAD軟件（CATIA、AutoCAD、UG等）與多種輻射輸運計算程序（MCNP、TRIPOLI[9］等）之間的接口。一方面，可以直接由計算機輔助設計（CAD）模型生成完整的輻射輸運計算程序的輸入模型，包括空腔模型、材料、源和計數信息等；另一方面，可以解析輻射輸運計算程序的輸入模型，生成CAD模型并可視化，供分析和修正。MCAM具有非常強大的幾何建模能力，能夠方便地建立各種復雜幾何的CAD模型。目前MCAM已經在一些復雜核裝置（如FDS系列聚變反應堆[10］、ITER 模型[11－13］等）的中子學建模和計算分析中得到了廣泛的應用。

本文基于MCAM提供的造型功能和內嵌的布爾運算功能，在MCAM平臺上進行二次開發了MOC幾何建模模塊，通過調用該模塊的接口，可以快速、精確地進行幾何建模，且能方便地構造出如反應堆燃料棒、燃料組件和反應堆堆芯等各種常見的幾何模型。同時，利用MOC建模模塊所構造的幾何模型可以通過調用MCAM底層的渲染接口在MCAM的GUI中渲染出來（如圖2），可非常清晰、直觀地表達出模型的幾何結構，便于用戶進行模型正確性檢查。同時，還為幾何模型添加了材料屬性編輯功能，即用戶可以對圖2中的幾何模型進行材料屬性添加，則MOC程序在進行輸運計算時，可以直接根據幾何模型的材料屬性來獲取材料的各種截面信息。最終構造好的幾何模型（已添加材料屬性）可保存為標準的CAD文件格式（sat，step，igs等），MOC 程序做中子輸運計算時可以直接將上述文件導入進行輸運計算，即本文開發的MOC程序支持CAD文件直接導入進行輸運計算的功能。

圖2 MCAM幾何建模Fig.2 Geometry modeling of MCAM

2.2 特征線跟蹤

由前面的特征線公式（1）～（5）可知，在進行特征線中子輸運計算時，需要不斷地進行特征線跟蹤來獲取模型的幾何和材料等相關信息。所以，MOC程序在進行中子輸運計算時所需要的幾何和材料等信息主要以特征線為載體，主要包括：特征線間距、特征線段長度、特征線所在網格編號、對應的材料號以及邊界信息等。本文主要基于MCAM提供的射線跟蹤功能，二次開發了MOC程序特征線自動處理模塊，圖3表示了整個MOC程序中幾何建模模塊、射線跟蹤模塊以及物理計算模塊等各模塊間的相互關系。

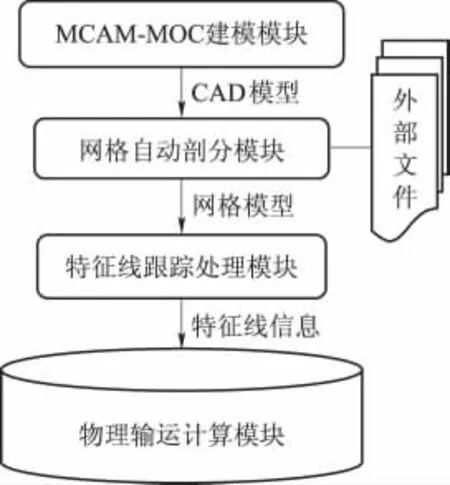
圖3 MOC程序模塊關系圖Fig.3 The relationship of different modules in MOC

在開始特征線跟蹤之前，程序根據用戶在外部配置文件中提供的方位角數目，自動進行方位角離散并計算每個方位角對應的特征線間距；然后根據網格劃分參數對模型進行網格劃分；最后根據已離散的方位角數值，通過調用MCAM的射線跟蹤接口來產生所有方位角下對應的特征線信息，并將之保存用于MOC程序的輸運計算。由于MCAM提供了射線跟蹤功能，并且計算精度和效率能保持在合理范圍內，在二次開發時可直接繼承這些功能進行應用程序的開發，大大提高了應用程序的開發效率。

3 數值驗證

本文提出了基于MCAM進行MOC幾何預處理的方法，并開發了特征線中子輸運計算MOC程序，為了驗證程序的正確性與可靠性，本文給出了一維7群例題和二維C5G7－UO2組件基準例題的數值驗證結果。

3.1 一維7群例題

本文采用文獻[14］中定義的一維7群問題，其幾何尺寸和材料布置如圖4所示，各種材料的7群截面來自C5G7－MOX基準題[15］。由于該問題材料間能譜差異大、泄漏較強，因此可以很好的驗證MOC程序的正確性。

圖4 一維7群例題幾何布置（cm）Fig.4 The layout of 1D7Gproblem（cm）

該問題的參考解由文獻[14］中的程序PEACH給出。表2給出了與PEACH程序計算結果的比較，其中本文采用平源菱形差分特征線法給出，平源區長度為0.1cm，方位角數目為4個，特征線間距約為0.05cm，從表1中可以看出本文計算的結果與參考值相比，keff誤差約為－3pcm，結果符合良好。

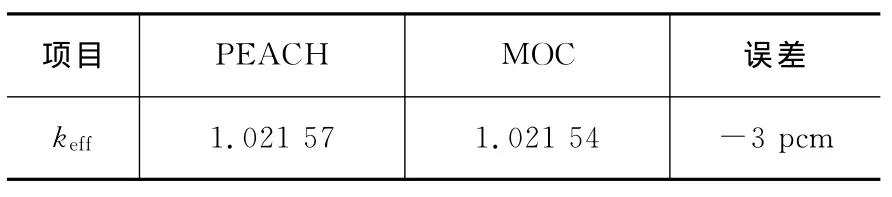
表1 一維7群例題MOC與PEACH結果比較Table 1 Comparision of kefffor 1D7G problem between MOC and PEACH

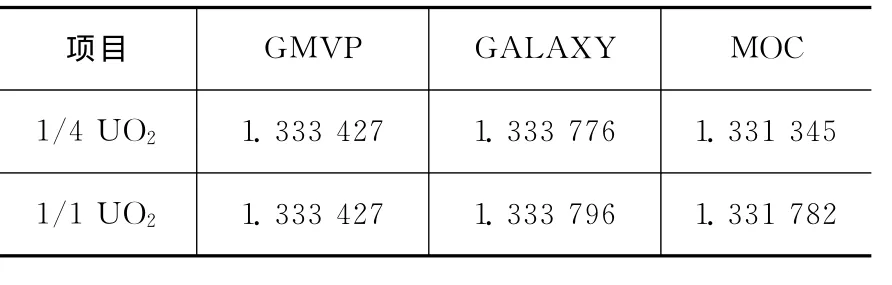
表2 二維C5G7－UO2組件例題kinf計算結果比較Table 2 Comparision of kinffor C5G7－UO2assembly results

在特征線方法中，影響計算結果精度的主要因素包括劃分網格尺寸大小、方位角數目、極角數目、特征線間距等。針對本例題，本文就前兩個因素做了敏感性分析。圖5給出了在不同網格劃分、相同角度離散（TY－2極角和4個方位角）、相同特征線間距（0.05cm）情況下keff誤差敏感性分析。從圖5可看出，網格大小對keff精度會有較大影響；當網格的尺寸小于1.0cm時，MOC程序能夠獲得非常滿意的計算精度（小于70pcm）。圖6給出了在相同網格尺寸（0.1cm）、相同極角離散（TY－2極角）、相同特征線間距（0.05cm）和不同方位角數目下keff誤差敏感性分析。從圖6中可以看出，當方位角數目N≥4時，繼續增加方位角數目對最終結果影響不大，誤差絕對值小于3pcm，故采用4個方位角已經可以獲得比較滿意的計算精度。

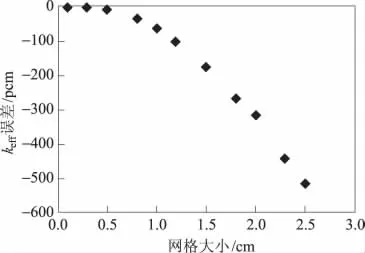
圖5 不同網格大小keff誤差分析Fig.5 kefferror analysis with different mesh dimensions

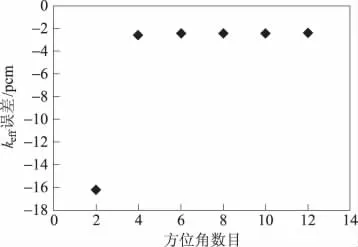
圖6 不同方位角數目keff誤差分析Fig.6 kefferror analysis with different angle dimensions

3.2 二維C5G7－UO2組件基準例題

二維C5G7－UO2基準題是國際經濟合作與發展組織（OECD）發布的二維C5G7基準例題[15］的二氧化鈾燃料組件，組件燃料布置與幾何結構如圖7所示。上圖為17×17個柵元組成的UO2組件，包括UO2燃料柵元、導向管柵元和裂變室柵元。柵元為兩區非均勻結構，各柵元的間距為1.26cm，柵元中的燃料芯塊和導向管均勻化后的半徑為0.54cm，組件四周采用全反射邊界條件。同時，采用圖7右下角的四分之一UO2燃料組件模型[16］進行進一步計算，通過和單組件計算結果對比，以進一步驗證程序的正確性。

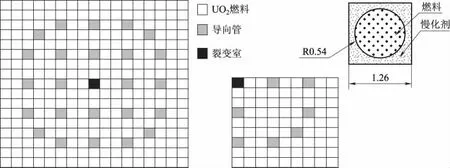
圖7 2DC5G7－UO2燃料組件幾何布置（cm）Fig.7 The layout of the 2DC5G7benchmark with UO2assembly （cm）

本文MOC程序計算時各材料區的截面信息采用文獻[15］中二維C5G7模型提供的宏觀截面數據。本文對1／4UO2組件和1／1UO2組件分別進行了kinf計算。在計算時，將模型進行非結構網格剖分；對空間角離散采用LO－2優化兩極角和6方位角離散；特征線間距為0.02cm，計算結果如表2所示。其計算結果與 程 序 GALAXY[16］、GMVP[17］的 誤 差 約 為－0.15%，說明與其他兩程序計算結果吻合良好；同時，MOC程序計算的1／4UO2組件和1／1UO2組 件 的kinf分 別 為 1.331 345 和1.331 782，相對誤差約為0.03%，兩模型計算結果符合良好，證明了本文MOC程序的正確性與可靠性。

總結

幾何預處理方法，即基于MCAM的幾何處理引擎，通過C＋＋語言面向對象二次開發了MOC幾何預處理模塊，可以非常方便地進行特征線幾何建模以及特征線信息快速獲取，這樣便將特征線理論與MCAM有效地結合起來。本文基于MCAM二次開發了特征線中子輸運計算MOC程序，并利用相關基準例題對程序進行了驗證，計算結果與國內外其他相關計算程序的結果吻合良好，表明本文方法和程序的可行性、正確性與可靠性。

致謝

本文在開展研究過程中，得到了西安交通大學劉宙宇博士在特征線理論方面的幫助與指導，在此深表感謝。

本文提出了一種基于CAD技術的特征線

[1]Askew R.A Characteristics for Mulation of the Neutron Transport Equation in Complicated Geometries[R］.Report AEEW－R－1108，UK Atomic Energy Authority，1972.

[2]吳宜燦，李靜驚，李瑩，等.大型集成多功能中子學計算與分析系統VisualBUS的研究與發展[J］.核科學與工程，2007，27（5）：72－85.

[3]吳宜燦，胡麗琴，龍鵬程，等.先進核能系統設計分析軟件與數據庫研發進展[J］.核科學與工程，2010，30（1）：55－64.

[4]Wu Y C，FDS Team.CAD－based Interface Prog－rams for Fusion Neutron Transport Simulation [J］.Fusion Engineering and Design，2009，84：1987－1992.

[5]吳宜燦，李瑩，盧磊，等.蒙特卡羅粒子輸運計算自動建模程序系統的研究與發展[J］.核科學與工程，2006，26（01）：20－27.

[6]李瑩，曾勤，盧磊.利用ITER基準模型對 MCAM4.2進行檢驗[J］.核科學與工程，2008，28（1）：47－50.

[7]Filippone W L， Woolf S，Lavigne R J.Particle Transport Calculation with the Method of Streaming Rays[J］.Nuclear Science and Engineering，1981，77：119.

[8]Yamamoto A，Tabuchi M，Sugimura N，et al.Derivation of Optimum Polar Angle Quadrature Set for the Method of Characteristics Based on Approximation Error for the Bickley Function [J］. Journal of Nuclear and Technology，2007，44（2）：129－136.

[9]張俊軍，曾勤，王國忠，等.蒙特卡羅程序TRIPOLI自動建模方法研究[J］.核科學與工程，2010，20（3）：84－88.

[10]Wu Y，FDS Team.Conceptual Design Activities of FDS Series Fusion Power Plants in China[J］.Fusion Engineering and Design，2006，81（23－24）：2713－2718.

[11]曾勤，盧磊，李瑩，等.蒙特卡羅粒子輸運計算自動建模程序MCAM在ITER核分析建模中的應用[J］.原子核物理評論，2006，23（2）：138－141.

[12]王國忠，黨同強，熊健，等.MCAM4.8在ITER建筑大廳中子學建模中的應用[J］.核科學與工程，2011，31（4）：351－355.

[13]熊健，王國忠，王電喜，等.MCAM 在ITER裝置TRIPOLI三維中子學建模中的應用[J］.核科學與工程，2011，31（2）：162－167.

[14]湯春桃.中子輸運方程特征線解法及嵌入式組件均勻化方法的研究 [D］.上海：上海交通大學，2009.

[15]Lewis E E，Simith M A，Tsoulfanidis N，et al.Benchmark Specification for Deterministic 2－D／3－D MOX Fuel Assembly Transport Calculations without Spatial Homogenization （C5G7MOX）[R］.NEA／NSC／DOC，2001.

[16]Yamaji K，Matsumoto H，Sato D，et al.Simple and Efficient Parallelization Method for MOC Calculation[J］.Journal of Nuclear Science and Technology，2010，47（1）：90－102.

[17]Mori T，Nakagawa T.MVP／GMVP：General Purpose Monte Carlo codes for Neutron and Photon Transport Calculations Based on Continuous Energy and Multigroup Methods [R］.Japan Atomic Energy Research Institute，1994.