基于塑性體積應變的梯度塑性理論研究

曾亞武，黎 玲，熊 俊，曹 源

(武漢大學土木建筑工程學院，武漢 430072)

1 研究背景

巖石是一種特殊的地質材料，其內部包含有大量的微裂紋。諸多實驗研究表明，巖石內部微缺陷的萌生、發育、擴展及至連接成核的一系列過程形成了巖石在外荷載作用下的宏觀應力－應變過程。當巖石材料變形到接近或超過峰值強度時，材料會出現局部的應變軟化帶，原來的均勻變形模式會被一種局限在某個很狹窄的帶狀區域內的嚴重不均勻的變形模式所代替，即產生很大的應變梯度，這種現象即所謂的應變局部化現象［1］。這種現象通常最先發生在材料內某些有限區域內，伴隨著局部化帶的發展而進一步擴展，它將直接導致材料的承載能力下降，也就必然導致巖土工程材料的承載力下降，故常常可以把它看作是材料局部破壞和結構失穩的一種先兆。

近年來，巖石應變局部化現象的研究已是國內外巖土界的研究熱點之一。至今，國內外相關領域的研究者圍繞應變局部化帶問題展開了一系列工作，很多重要理論如局部化分叉理論、廣義空隙壓力理論、復合體理論、Cosserat理論、非局部理論、梯度塑性理論等在應變局部化研究中得到應用和發展。在這些理論方法中，梯度塑性理論引入非局部化的思想，將軟化參數的梯度項引入到材料的屈服模式中，考慮了一點周圍介質點的應力狀態對該點的影響，解決了應變局部化分析中的網格依賴性問題。從梯度塑性理論的角度出發，對巖石應變局部化現象進行相關研究將有著重要的應用價值和工程背景;而且，基于梯度塑性理論的巖石應變局部化研究問題在學術上具有很大的挑戰性，長遠看來，它也必將推動彈塑性力學理論、有限元計算理論等的發展。

2 梯度塑性理論的分類

目前，對梯度塑性理論的研究可分為2類:應變梯度塑性模型與內變量梯度塑性模型。

2.1 應變梯度模型

在材料每一個質點上的變形不僅取決于通常意義的應變(與位移一階梯度相關)，還取決于應變梯度(與位移二階梯度相關)。一般情況下，這類模型也可以考慮二階或高階的應變梯度項。

2.2 內變量梯度模型

引進與某個熱力學力相共軛的內變量梯度，熱力學力只出現在內變量的演化方程中，在平衡方程中不出現。這類模型不改變平衡方程，只須修改本構方程，給數值計算帶來了很大的便利。在彈性范圍內，內變量不會變化而始終保持為初始值(通常為零)。因此，內變量梯度模型的初始響應由標準的彈性力學理論決定，而只有在非彈性階段才會有梯度效應。

2.3 兩者之間的差別

2類梯度塑性模型的根本區別在于，應變梯度模型中的應變梯度被看作是附加的可觀察狀態變量，這類變量與平衡方程中的高階應力共軛;而內變量梯度模型中的內變量梯度與某些耗散熱力學力共軛，它們作為內變量出現在演化方程中，但是不會出現在平衡方程中。因此，內變量梯度塑性理論僅僅修正塑性模型本構方程的基本形式，而運動學方程和平衡方程仍然保持不變。從熱力學角度來講，可以說內變量梯度塑性理論僅僅提高了潛在的熱力勢和耗散能，而應變梯度理論既需要對內力功也需要對外力功進行概括。

當然，某些模型也可能會帶有混合的性質。例如，Zervos等［2］提出的梯度塑性模型，既可以被理解為應變梯度塑性模型，也可以被認為是包含內變量的二階梯度的軟化流動塑性模型。

3 應變局部化的梯度塑性理論研究

3.1 梯度塑性理論一般本構關系

經典的塑性理論認為，對于各向同性材料，材料的屈服函數可寫為

式中κ為硬化參數(這里的硬化是包含軟化在內的一個廣義概念)，它可采用塑性功或等效塑性應變等內變量表示。梯度塑性理論在此基礎上引入了非局部化思想，認為一點的屈服不僅與自身的應力狀態和硬化參數相關，還與相鄰點的硬化參數有關。它將硬化參數的梯度項引入到材料的屈服函數中，使一點的屈服極限還受相鄰區域硬化參數的影響，這樣其影響區域的大小將由所給定材料的內部特征長度決定。

唐天國等［3］基于經典塑性理論，結合梯度塑性理論的特點，以非局部硬化參數代替傳統屈服函數中的局部硬化參數，推導出了梯度塑性理論的一般本構關系

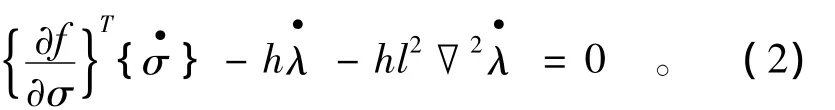
3.2 內變量梯度塑性模型

由(2)式可知，在引入硬化參數的梯度項之后，一致性條件變為一個關于塑性乘子的偏微分方程，無法寫出塑性乘子在局部意義上的顯式表達式，進而也無法寫出單元切線剛度矩陣的顯式表達式。為了使計算結果接近真實的數值解，必須使用適當的正則化方法以防止應變變成一系列的零值。Lasry和Belytschko［4］在應變－位移關系中引入了位移的高階梯度項;Fleck和Hutchinson［5］將高階應變梯度作為附加的、可觀測的狀態變量;Aifantis［6］，Muhlhaus等［7］在非彈性本構方程中引入了描述非彈性變形的內變量的某種梯度，在材料模型中引入了作為正則化機制的內部長度參數。

考慮到巖石材料的特殊性，以塑性體積應變為內變量，在Drucker-Prager屈服模式下引入其梯度項，建立內變量梯度塑性模型。

3.2.1 塑性體積應變

按照經典彈塑性理論，在應力空間中巖石的屈服函數可以表示為

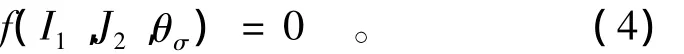
式中:I1是主應力第一不變量;J2是偏應力第二不變量;θσ是羅德角。按照復合求導法則可得

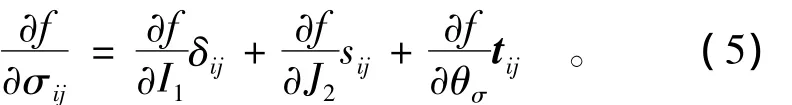
式中:δij是 Kronecker符號;sij為偏應力;tij是偏張量，且

其中:sim，smj也均為偏應力。

使用關聯流動法則，可知塑性應變增量為

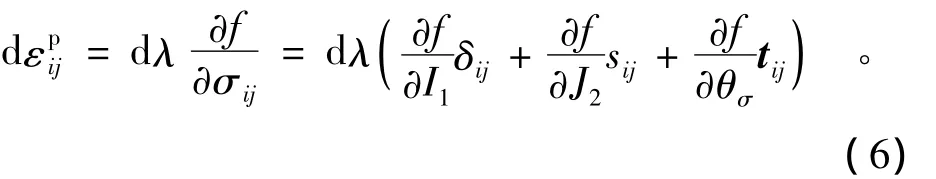
式中:dλ是1個非負的比例因子(表示塑性應變增量的大小)，上式括號中第1項反映塑性體積應變增量，而第2，3項反映塑性偏應變增量，即

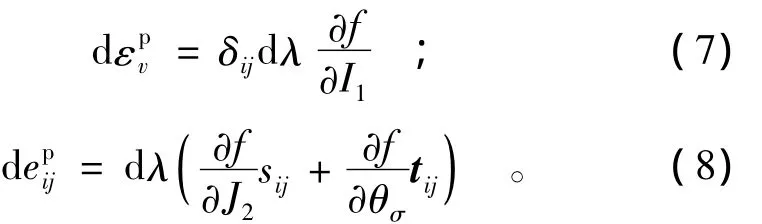
對于巖石材料而言，屈服后的加載過程中，由于塑性變形不斷增加，引起加載面不斷改變，硬化程度取決于塑性加載歷史，使用內變量來描述，于是，加載面的改變取決于應力狀態和內變量。而在其變形過程中塑性體積變形的影響非常顯著，應用塑性體積應變來定義內變量更利于反映體積應力與塑性體積應變的關系。

3.2.2 巖石應變局部化增量本構關系

材料內總應變與彈性應變和塑性應變之間存在以下關系:

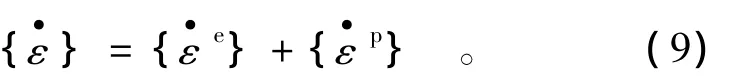
在本模型中，選用考慮體積力對塑性變形產生影響的Drucker-Prager屈服函數:

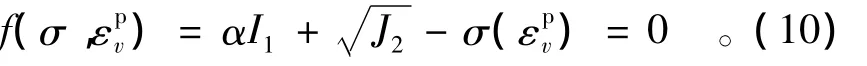
由式(8)得到此時塑性偏應變增量為

為了簡便，假定巖石在單軸壓縮狀態下，其本構關系為雙線性，即峰值強度之前為線彈性，超過峰值強度后為線性應變軟化，降模量為一個常值λ'，如圖 1 所示。用，σ)分別代替單軸壓縮下應力-塑性應變關系式中的塑性應變和應力，得到 σ()的表達式為

圖1 單軸壓縮線性軟化模型Fig.1 Linear softening model in uniaxial compression

根據梯度塑性模型，在巖石各向同性假設下，可得如下關系:

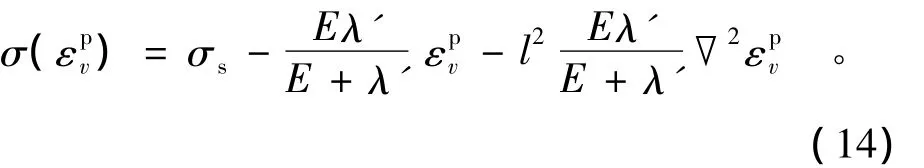
由于l為材料的內部特征長度，于是式(10)變為

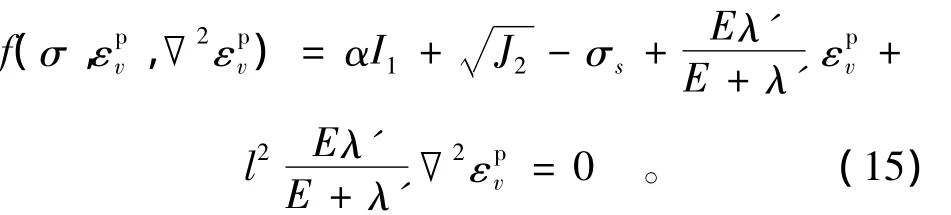
采用相關流動法則，有

而由式(11)有

結合式(15)、式(16)與式(17)，可得巖石應變局部化的增量本構關系為

式中:D為彈性矩陣。

3.3 平面應變下單向受力巖石應變局部化分析

3.3.1 應變局部化帶寬度公式推導

假定巖石在單軸壓縮狀態下，壓應力大小為σ0。由Drucker-Prager屈服函數得

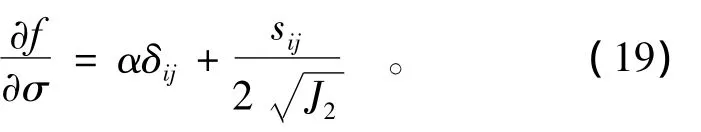
設由上式得到的各應力分量流動方向分別為

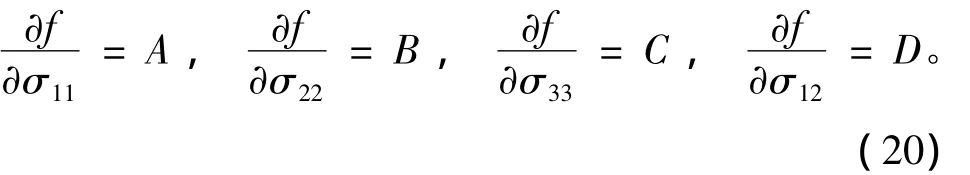
考慮平面應變情況，將平面應變情況彈性矩陣D代入式(18)，得應力率為:

式中:G為剪切模量;μ為泊松比。

由一致性條件及屈服條件(15)并結合式(21)化簡得

式中:

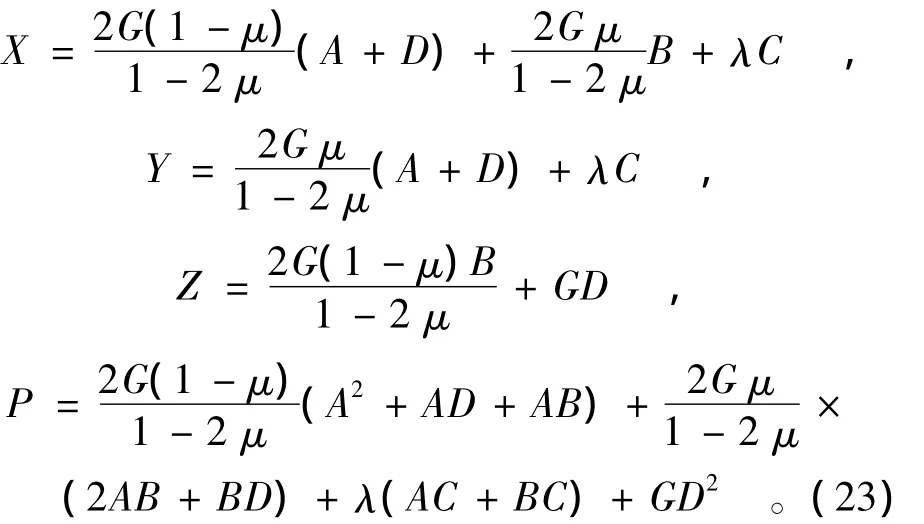
考慮到應變局部化發生過程中產生的顯著體積變化，在單軸壓縮平面應變情況下，考慮應變局部化區域內產生的體積擴容，設擴容系數為ξ，并有如下關系存在

將式(24)代入式(20)第二項，得到

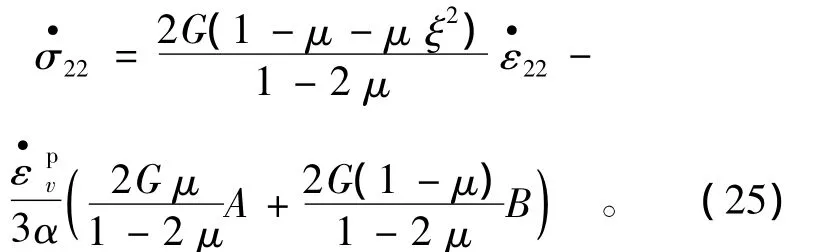
由于平面應變條件下σ22的變化很小，可以認為，于是由式(25)可得

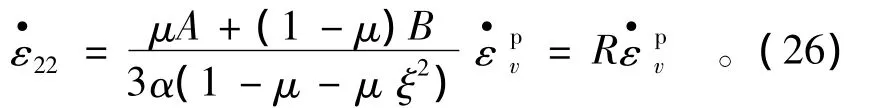
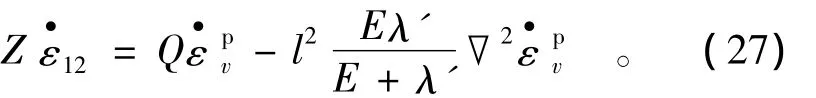
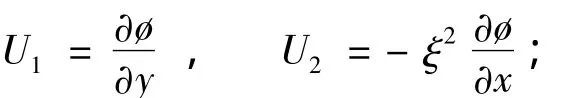
假設巖石試樣在外荷載作用下形成的應變局部化帶寬度為w，傾角為θ，非應變局部化帶區域仍為彈性變形。引入一個垂直于應變局部化帶的坐標系XoY，如圖2所示。則該坐標系與現有xoy坐標系之間的轉換關系為:

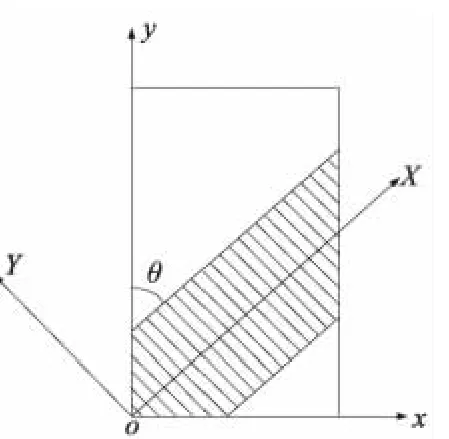
圖2 坐標轉換示意圖Fig.2 Coordinate conversion

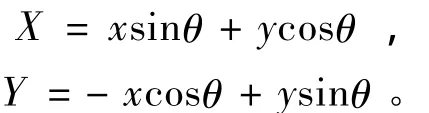
假設應變局部化帶內參數僅沿帶的Y方向發生變化，而在X方向是均勻不變化的，則:

將式(29)代入式(26)，得

將式(30)代入式(29)，得

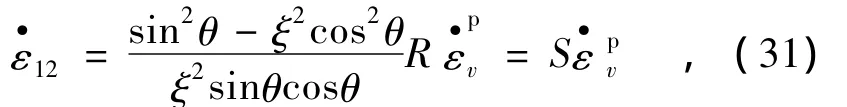
將式(31)代入式(17)，并簡化得

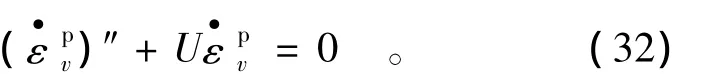
下面將討論方程(32)的解，分以下2種情況討論。

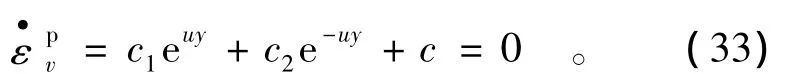
求解式(34)，得

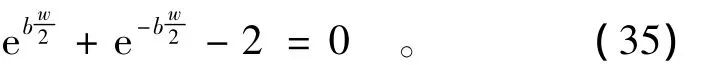
由于b≠0，要使式(35)有解，則w=0，這與實際明顯矛盾，故U＜0的情形下無解。

(2)當U＞0時，令U=u2，同上得方程的解為

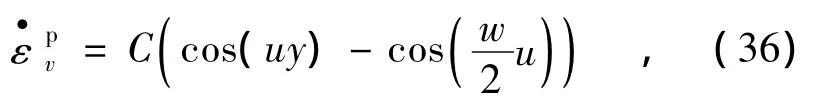
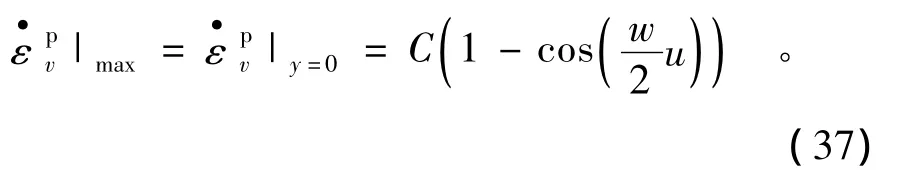
于是有wu/2=π，由此可以得到應變局部化帶的寬度表達式為

3.3.2 局部化帶參數對局部化帶寬度的影響

由式(38)可看出，巖石試件應變局部化帶的寬度是隨著應變局部化過程的發展不斷變化的。又易知

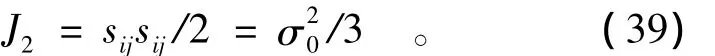
于是由式(19)可得:

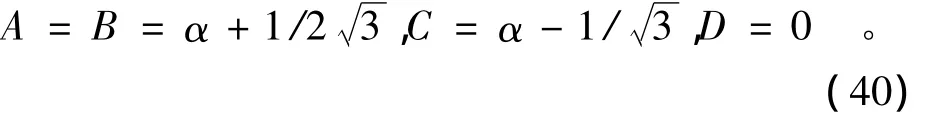
將式(40)分別代入式(23)與式(26)中，并化簡可得:

于是式(32)中的U為

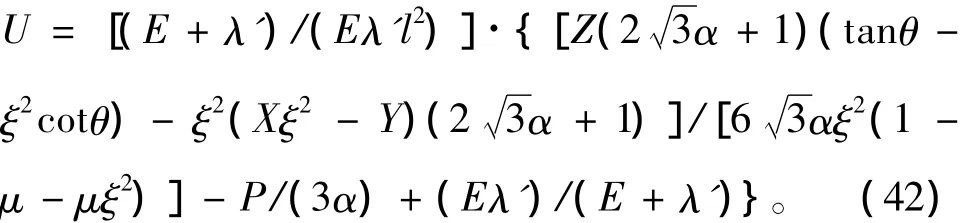
由式(41)及式(42)可看出:在U的表達式中，E，λ'，l，G，μ，α，ξ均為常數，θ為應變局部化帶傾角。當U取最大值時，應變局部化帶寬度w最小，應變局部化開始發生，此時的θ表示初始局部化帶傾角。當U取最小值時，w最大，巖石已經發生破壞，此時的θ表示巖石破壞時對應的傾角。

4 結論

本文引入了梯度塑性理論的一般本構關系，將塑性變形梯度引入材料的本構方程中，說明梯度塑性理論中具有能夠表征材料內部特征長度尺寸的長度量綱。考慮到巖石材料在受到外荷載作用時內部體積變形的特殊性，嘗試采用以塑性體積應變作為內變量，建立內變量梯度塑性模型進行巖石應變局部化的研究，并從經典塑性理論下的屈服函數一般形式出發推導了塑性體積應變的表達式。在此基礎上，還推導了巖石應變局部化增量本構關系，并在Drucker-Prager屈服函數下寫出了塑性體積應變的具體形式，將其梯度項引入巖石材料的屈服關系中對其應變局部化問題進行研究。在平面應變條件下，分析了巖石試樣受單軸壓縮作用應變局部化的發生發展情況，得到其應變局部化帶寬度的一般表達式，并對其進行分析討論。

［1］王學濱，潘一山.地質災害中的應變局部化現象［J］.地質災害與環境保護，2001，12(4):1－5.(WANG Xue-bin，PAN Yi-shan.Strain Localization Phenomenon in Geological Disaster［J］.Journal of Geological Hazards and Environment Preservation，2001，12(4):1 － 5.(in Chinese))

［2］ZERVOS A，PAPANASTASIOU P，VARDOULAKIS I.A Finite Element Displacement Formulation for Gradient Elastoplasticity［J］.International Journal for Numerical Methods in Engineering，2001，50(6):1369 －1388.

［3］唐天國，謝新生，段云嶺.高地應力場巖體深部卸荷斷裂帶的梯度項塑性算法分析［J］.水力學報，2011，12(42):1432 － 1437.(TANG Tian-guo，XIE Xin-sheng，DUAN Yun-ling.Analysis of Gradient-Plasticity Algorithm for Deep Unload Rock in High Ground Stress Field［J］.Journal of Hydraulic Engineering，2011，12(42):1432 －1437.(in Chinese))

［4］LASRY D，BELYTSCHKO T.Localization Limiters in Transient Problems［J］.International Journal of Solids and Structures，1988，24(6):581 －597.

［5］FLECK N A，HUTCHINSON J W.Strain Gradient Plasticity［J］.Advances in Applied Mechanics，1997，33:295－361.

［6］AIFANTIS E C.On the Microstructural Origin of Certain Inelastic Models［J］.Journal of Engineering Materials and Technology，1984，106(4):326 －330.

［7］MUHLHAUS H B，ALFANTIS E C.A Variational Principle for Gradient Plasticity［ J］.International Journal of Solids and Structures，1991，28(7):845－857.