基于開關變壓器的高壓異步電動機軟啟動的仿真研究

耿大勇，李亮之，魏 玲，朱延楓，王 巍

（遼寧工業大學電氣工程學院，遼寧錦州121001）

1 引言

隨著經濟的發展，許多行業的生產規模越來越大，使用高壓異步電動機（3～10kV）的數量漸增，單機容量也越來越大。電機直接全電壓啟動因啟動電流過大對電機本身及電網會帶來嚴重影響，故高壓異步電動機的啟動一直是人們所關心的一個課題，目前多采用軟啟動方式。近幾年來，一種帶有開關變壓器的高壓異步電動機軟啟動器得到廣泛應用，該軟啟動器是用變壓器來隔離高壓和低壓，解決了晶閘管的耐壓限制問題，有廣闊的應用前景［1-4］。關于開關變壓器式高壓異步電動機軟啟動器的結構設計、工作原理及應用已有文獻給予闡述［1-2］，但關于這種軟啟動控制系統數字仿真的文獻較少，本文構建了基于開關變壓器的高壓異步電動機軟啟動控制系統的數學模型并進行了實例仿真及分析。最后進行了系統實驗，以驗證仿真方法的正確性。

2 軟啟動系統結構及工作狀態分析

基于開關變壓器的高壓異步電動機軟啟動控制系統的電路結構框圖如圖1所示［3］，晶閘管不是串在電機的定子回路中，而是用變壓器來隔離高壓和低壓，變壓器的高壓繞組串在異步電動機的定子回路中，而低壓繞組和一對反向晶閘管并聯。假設開關變壓器為理想的變壓器，其勵磁阻抗為無窮大。當晶閘管未導通時，變壓器工作在空載狀態，所以電網電壓都降在變壓器原邊繞組上，電機不能啟動。當晶閘管觸發導通時，其導通壓降可忽略，在這種情況下，加在變壓器繞組兩端的電壓可以認為為零，則電網電壓都加于電動機定子端部，基于上述的假設，則該系統的變壓器僅起到理想開關的作用。啟動時，通過控制系統控制晶閘管的觸發角，可以連續改變低壓繞組上的電壓，進而改變高壓繞組的電壓而達到連續改變電機端電壓的目的。軟啟動電壓和電流波形示意圖如圖2所示。其中uA、uB和uC分別為A、B、C三相對稱電源的電壓，iA、iB和iC分別為電機定子的A、B、C三相電流。異步電動機為感性負載，故iA落后于uA一個φ角，圖中也示出了晶閘管的觸發角α和關斷持續角λ。軟啟動運行過程，實際上是電機定子繞組以不同的電路拓撲結構接向電源的過程。如圖2所示，為便于分析，將一個周期分成6個相等的間隔T1～T6。詳細分析T1～T6每個間隔內各個晶閘管導通和關斷的情況，將發現異步電動機在對稱運行中表現出某種重復規律。根據關斷持續角λ的不同，一個對稱區間內將由兩種不同導通情況構成。

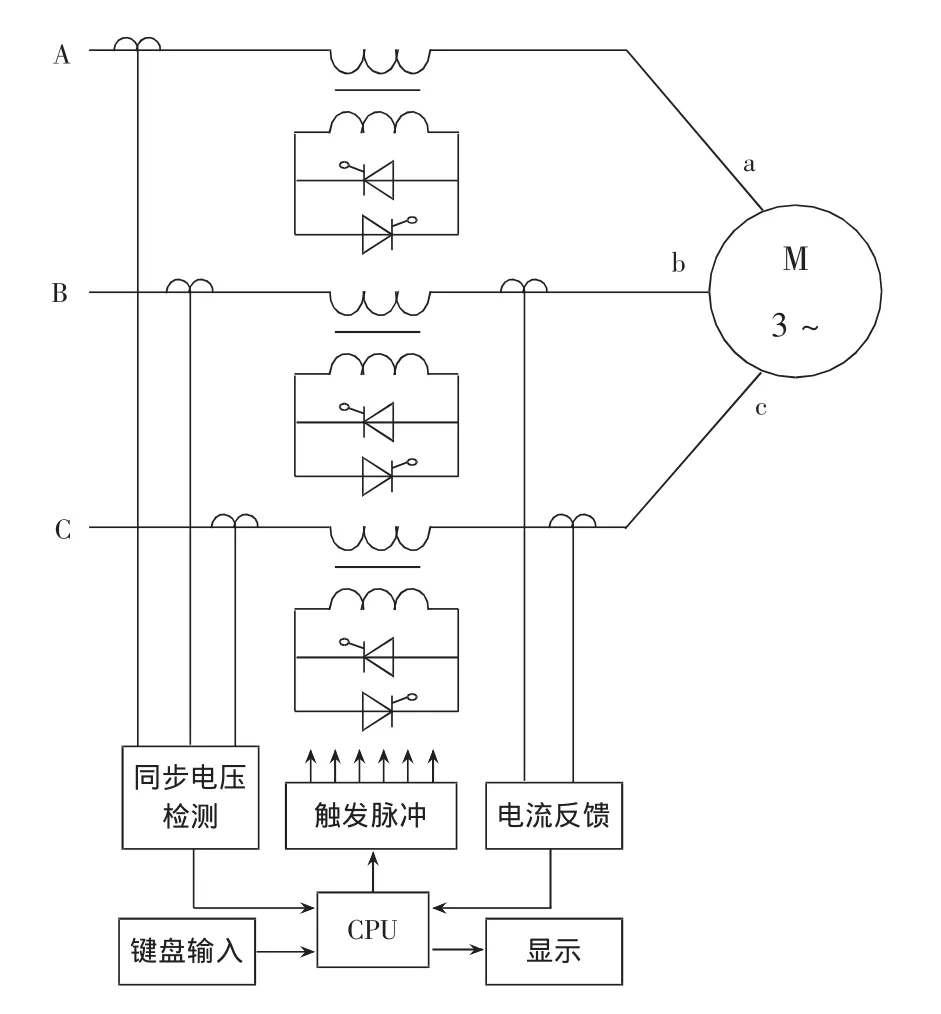
圖1 高壓異步電動機軟啟動控制系統的電路結構

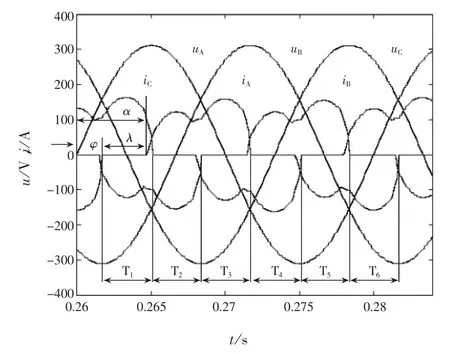
圖2 軟啟動電壓和電流波形

（1）當0≤λ≤π／3時，對稱區間內由三相導通狀態和兩相導通狀態構成。為詳細分析這種情況下電機的運行規律，先具體規定電機的4種工作狀態，狀態①：三相電源同時導通；狀態②：A相的電源關斷，B、C相電源導通；狀態③：B相的電源關斷，A、C相電源導通；狀態④：C相的電源關斷，A、B相電源導通。在T1～T6的間隔內，系統將依次處于上述的②、①、④、①、③、①幾種狀態。

（2）當λ＞π／3時，對稱區間內將由兩相導通狀態和三相均不導通狀態構成。這種情況下除了出現狀態②、③、④外，還會有狀態⑤：三相均不導通。這種情況下系統將依次處于②、⑤、④、⑤、③、⑤狀態。

3 仿真數學模型的建立

3.1 狀態方程的建立

運行狀態確定后，下面建立仿真所用數學模型，本文對異步電動機動態過程的分析求解采用狀態變量法進行。設定子A相與轉子a相軸線之間夾角為θ，轉子以機械角速度Ω逆時針旋轉，則異步電動機的電壓方程為：

式中：u、i、R和L分別為電機定子和轉子的端電壓矩陣、電流矩陣、電阻矩陣和電感矩陣。異步電動機的轉矩方程為：

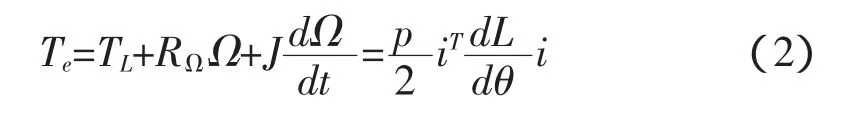
式中：TL、Ω、J、RΩ和 p 分別為電機的負載轉矩、機械角速度、轉動慣量、旋轉阻力系數和極對數。

將（1）、（2）式變形，再結合得出：

則可得到以電流向量i、機械角數度Ω和轉角θ為狀態變量的異步電動機狀態方程為：

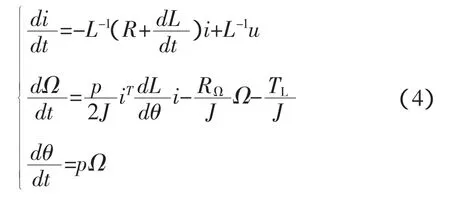
上式可簡寫為：

其中x為狀態向量，U為輸入向量，A和B為系數矩陣，分別為：

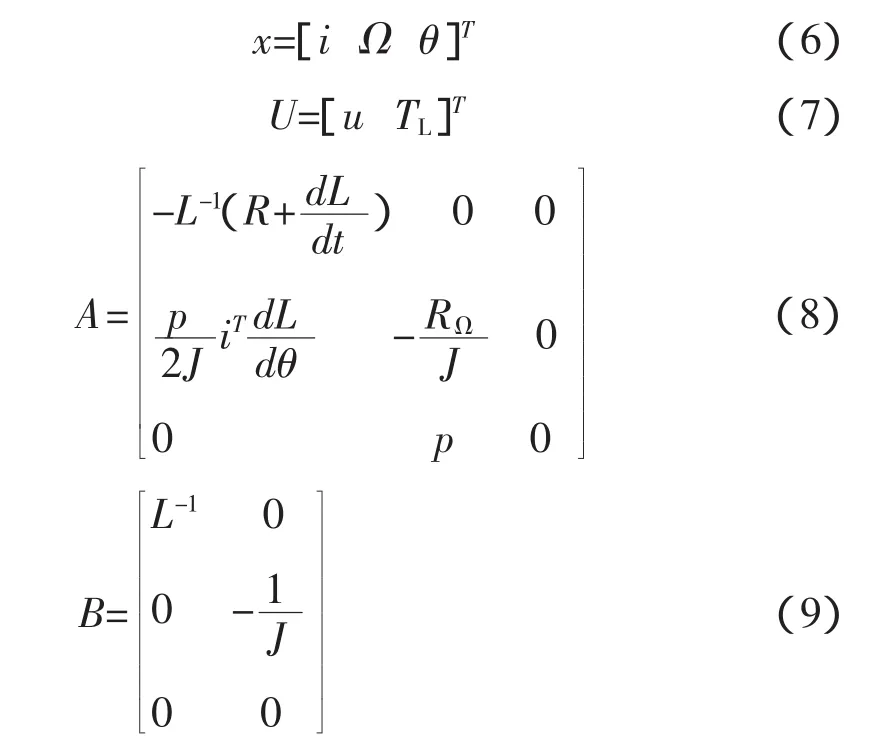
式（5）即為異步電動機狀態變量法仿真數學模型的標準形式。為了便于對其求解，假定電動機的全部參數為常數，忽略磁飽和。

3.2 狀態方程求解中對電動機輸入電壓的處理

因電動機轉子短路，轉子端電壓可認為為零，故在對高壓異步電動機軟啟動狀態方程的求解中，關鍵是對于定子輸入電壓的處理。下面就電動機的各個工作狀態進行說明。

3.2.1 狀態①

當電機運行于狀態①時，電機定子的各相電壓即為各相電源電壓。

3.2.2 狀態②

狀態②為電動機A相斷線的情形，此時對不對稱的定子輸入電壓的處理采用了對稱分量法。據電機學理論，可以將不對稱的電源電壓和分解成正序、負序和零序三組對稱電壓，即：

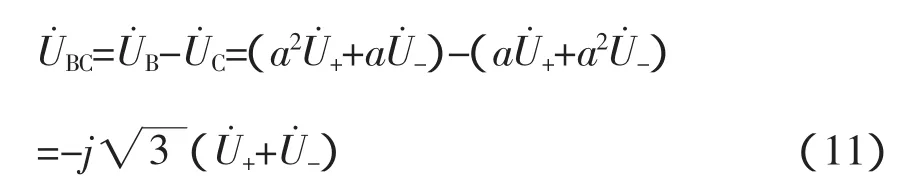
正序、負序電流分別為：

由式（12）及（13）可把電動機正序和負序等效電路反向串聯，如圖3所示。由式（11）求得：

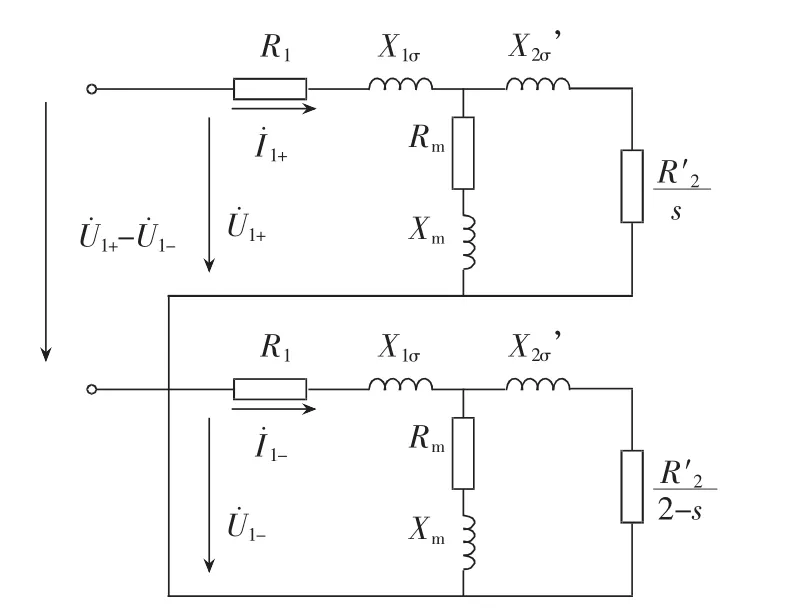
圖3 正序和負序等效電路反向串聯的示意圖

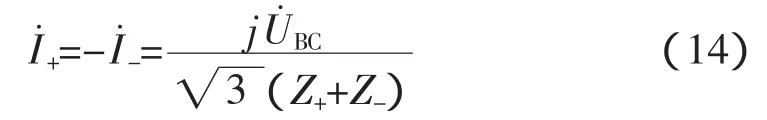
式中：Z＋和Z-分別為電動機的正序和負序阻抗，由圖3容易求得。圖3中R1和X1σ分別為定子每相電阻和漏電抗；R2’和X2σ’分別為轉子每相折算電阻和折算漏電抗；Rm和Xm分別為激磁電阻和激磁電抗。則正序、負序電壓為：

將上式代入式（10）便可求出加在電機三相繞組上不對稱的電源電壓和另外求解狀態方程時要加上強迫約束條件為和

3.2.3 狀態③

狀態③為電動機B相斷線的情形，仿照狀態②的分析過程和方法，此時有：

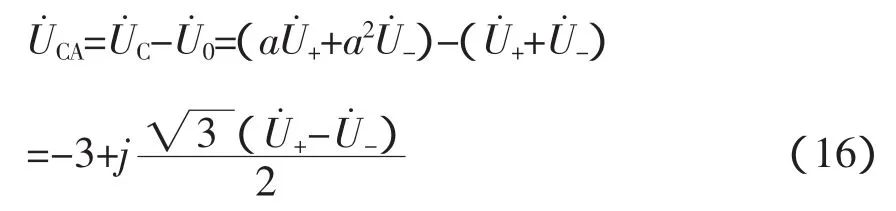
3.2.4 狀態④

狀態④為電動機C相斷線的情形，同樣仿照狀態②的分析過程和方法，此時有

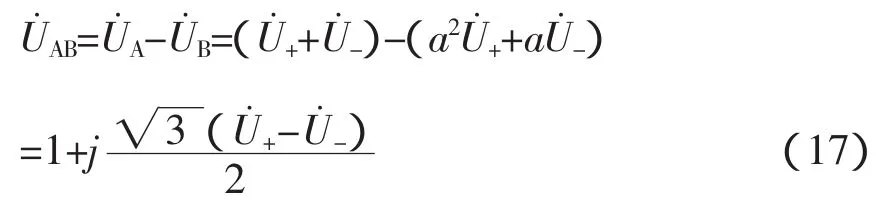
3.2.5 狀態⑤

因三相均不導通，故定子輸入電壓和三相電流均為0。

4 軟啟動控制方式及仿真結果分析

對高壓異步電動機軟啟動仿真采用電流閉環控制的斜坡恒流軟啟動方式，啟動電流上升變化率和電流限定值都可任意設定。控制系統中的電流反饋量取自電動機相電流有效值，和限定電流的給定值作比較，經比例積分運算得到調整后的觸發角去觸發晶閘管導通以實現電動機按預定的規律軟啟動。輸出的晶閘管觸發角計算公式為：

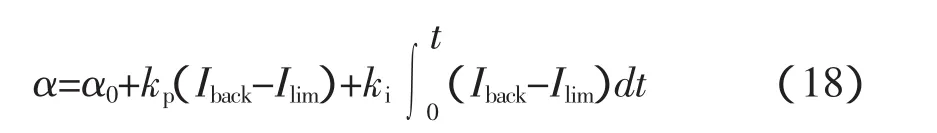
式中：α為當前輸出的晶閘管觸發角；α0為初始給定的晶閘管觸發角；kp為比例常數；ki為積分常數；Ilim為啟動電流限定值；Iback為啟動電流反饋值。仿真軟件的程序框圖如圖4所示。

圖4 軟起動程序框圖

以一臺實際的高壓異步電動機為例進行了仿真，電機參數如下：PN＝330kW，UN＝6000V，IN＝40A，定子電阻 R1＝1.22Ω，轉子折算電 R2’＝3.01Ω，鐵耗等效電阻 Rm＝4.72Ω，定、轉子互感 Lm＝0.18H，定、轉子漏電感 L1σ＝L2σ’＝0.006H，轉動慣量 J＝14.5kg·m2，極對數p＝2。觸發角PI調節器模型中設限定電流為2倍的額定電流左右，取為80 A，積分常數ki取為0.05，比例常數kp取0.07，給定初始觸發角α0為100°，電機負載率為10%額定負載。

仿真結果如圖5所示。其中圖5（a）顯示了用有效值表示的電機直接啟動和軟啟動過程中相電流變化情況。圖5（b）為軟啟動過程中電機相電流仿真波形。由圖5可見，直接啟動時瞬時沖擊電流很大，而軟啟動時的啟動電流能夠限制在期望值下且接近恒流啟動。啟動過程平穩，不存在震蕩現象。

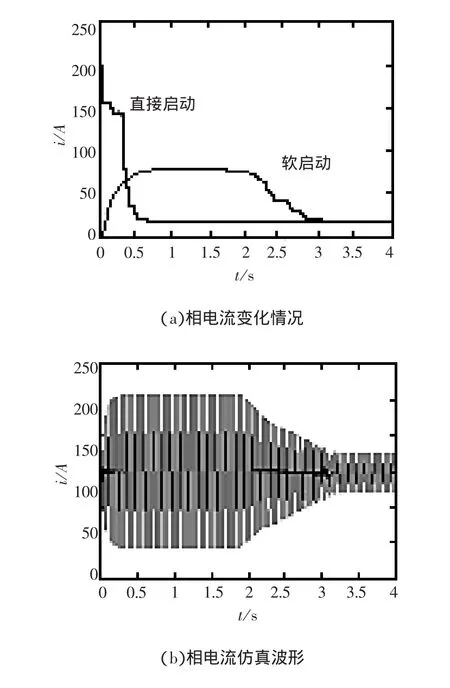
圖5 仿真結果

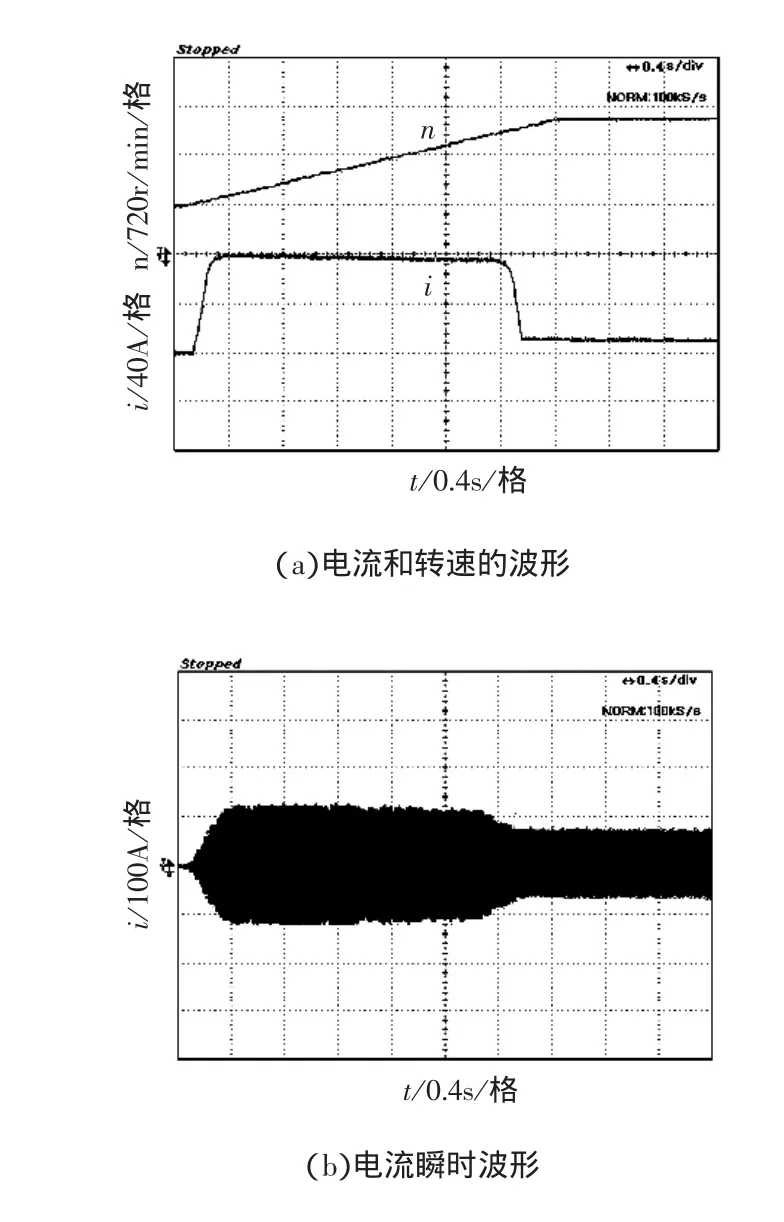
圖6 軟起動實驗結果

5 實驗驗證及結束語

利用前面介紹的高壓異步電動機軟啟動的控制方法對仿真用電機進行了軟啟動實驗，實驗結果如圖6所示。其中圖6（a）示出2倍額定電流下軟啟動時電流（整流并轉化為電壓信號）和轉速的波形。圖6（b）示出軟啟動過程電流的瞬時波形。在整個啟動過程中啟動電流基本維持在設定值附近，而電機轉速逐漸上升，達到了預期的軟啟動效果。實驗結果和仿真結果吻合，驗證了仿真方法和控制方法的正確性和有效性。以本文建立的基于開關變壓器的高壓異步電動機軟啟動控制系統仿真模型為基礎，可進一步進行其他軟啟動方式的建模仿真及對比優化研究，對實際高壓異步電動機軟啟動控制系統的研制有一定的指導意義，有工程實用價值。

［1］甘世紅，褚建新，顧 偉.基于限流變壓器的高壓異步電機軟啟動控制器［J］.電力電子技術，2005，39（3）：59-60.

［2］甘世紅，褚建新，顧 偉.基于開關變壓器的中壓異步電動機軟啟動器［J］.中國電機工程學報，2005，25（16）：153-157.

［3］甘世紅，褚建新，顧 偉.高壓異步電動機軟啟動器的簡化等效數學模型和實驗［J］.電工技術學報，2006，21（7）：89-93.

［4］甘世紅，吳燕翔，褚建新，顧 偉.高壓（3-10kV）電機軟啟動模糊控制器［J］.武漢理工大學學報（交通科學與工程版）2007，31（6）：1029-1032.

［5］高景德.交流電機及其系統的分析［M］.北京：清華大學出版社，1992：428-430.

［6］Gurkan Zenginobuz，Isik Cadirci，Muammer Ermis.Soft starting of large induction motors at constant current with minimized starting torque pulsation［J］.IEEE Transaction On industry Applications.2001，（9）：61-64.