雙邊永磁同步直線電動機磁阻力分析及最小化
常九健,馬文禮,黃金龍
(中國科學院光電技術研究所,四川成都610209)
0 引 言
隨著現代加工技術的不斷進步,高精度、大推力的永磁同步直線電動機在國防、運輸、機械加工等領域得到了廣泛的應用[1]。與直線感應電機相比,永磁同步直線電動機具有力能指標高、體積小、重量輕等優點[2]。尤其是雙邊永磁同步直線電動機(如圖1所示),克服了單邊直線電動機存在垂直于運動方向吸引力的缺點,同時可以將水平推力增大到單邊時的兩倍。但是該種電機在運行過程中存在較大的推力波動,推力波動可能造成電機振動與噪聲,尤其是當電機速度比較低時,容易引起機械共振,從而惡化其運行特性。因此,分析電機的推力波動對于研究其運行特性就顯得至關重要,同時該方向也是學術界研究的熱點之一[3]。造成永磁同步直線電動機推力波動的因素有很多,其中最主要的是磁阻力,磁阻力主要是由于電機初級鐵心長度有限形成的邊端力和采用具有齒槽結構的初級鐵心而形成的齒槽力[4-6]。

圖1 雙邊永磁同步直線電動機
本文主要采用有限元方法來優化電機結構從而來減小電機的力矩波動。優化前電機相應參數如表1所示。由于采用三維有限元分析需要花費大量的時間,且電機上下關于初級鐵心對稱,本文在不考慮電機橫向邊端效應的前提下沿永磁體排列方向截取電機的一個截面,選取截面的下半部分對電機模型進行二維有限元分析,如圖2所示。
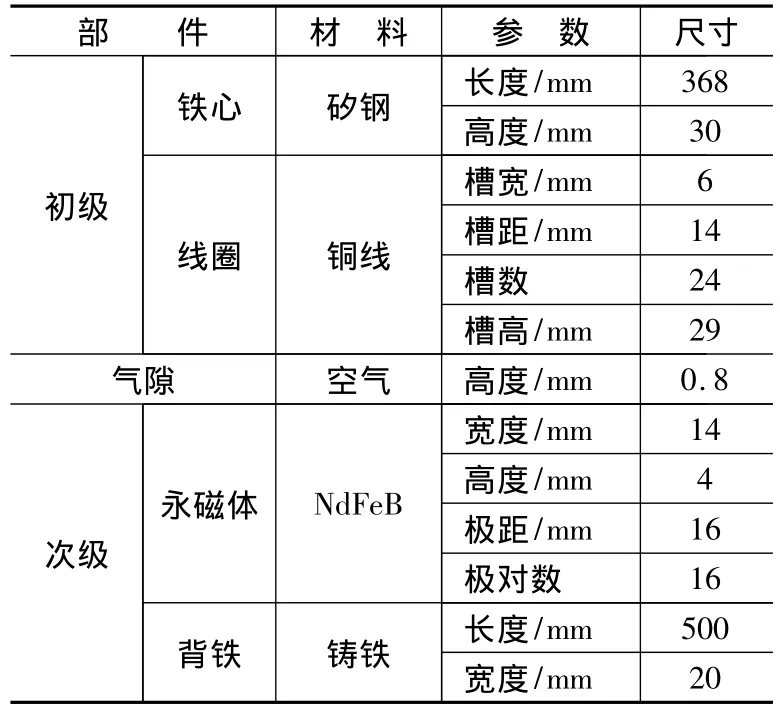
表1 電機參數

圖2 電機二維有限元模型
1 永磁同步直線電動機磁阻力分析
1.1 永磁同步直線電動機邊端力分析及優化
與旋轉電機不同的是直線電機的鐵心長度為有限長,在鐵心的開斷處由于導磁介質不同,磁導率就會發生突變,從而引起磁場的突變,造成力矩波動。由文獻[7]可知,初級鐵心受到的邊端力是次極極距的周期函數,在實際情況中,齒槽效應和邊端效應是同時存在的,為了避免齒槽效應對分析結果的影響,本文分析邊端效應時采用一種無槽的電機模型,如圖3所示。

圖3 電機邊端效應模型
通常情況下,初級長度比較長時(3~4極距以上),兩邊端基本上無相互影響[8],因而圖3中的模型受力情況等效為兩個半無限長初級鐵心單端受力的合成結果。等效的兩個無限單端鐵心結構,受力等大反向,即一端為正,另一端為負,但是由于兩邊端力之間存在相位差,因此合成的邊端力不為零。兩邊端力之間的相位差取決于初級鐵心的長度,通過優化初級長度的方法來使左右兩端的推力相互抵消,從而減小力矩波動。
由以上分析可以得到:
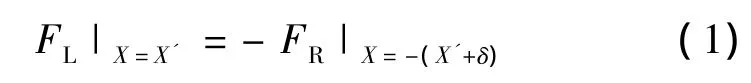
式中:FL、FR分別為初級鐵心左右兩端受力大小;δ=kτ-Ls;k為任意整數;τ為極距;Ls為初級長度。將左邊端力用傅里葉級數表示:
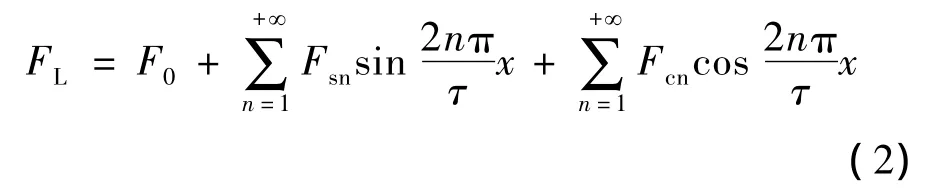
由式(1)、式(2)可得:
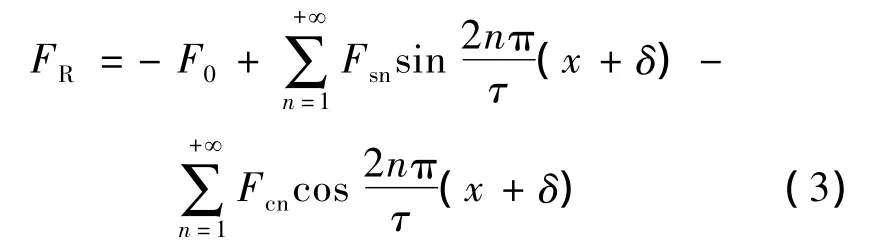
整體邊端力大小可以看作是兩個半邊端力的合力,即:
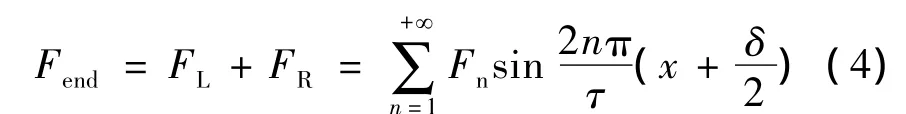
式中:
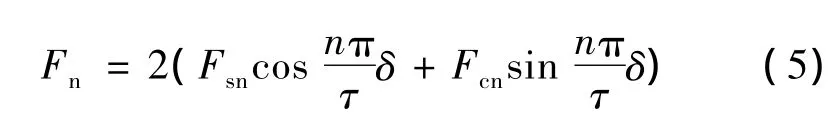
由以上分析可知,若要使邊端力Fend最小,可以通過選擇合適的鐵心長度減小邊端力的幅值,即使Fn達到最小,即:
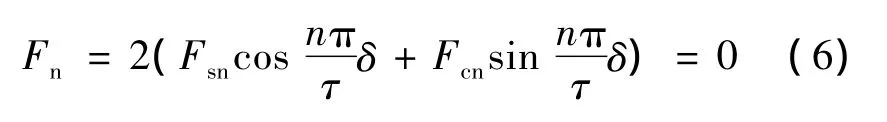
則使邊端力最小的優化δ值:
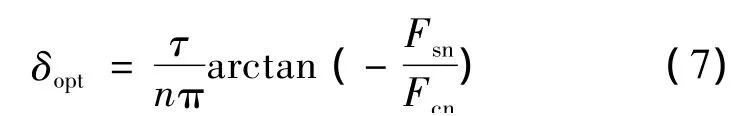
但是實際上由于邊端力Fend是各階諧波的和,因此不能完全使邊端力Fend完全等于零,只能將其減到最小。要將邊端力減小到最小,需要分析邊端力曲線中各次諧波占的比重,只有消除占比重大的諧波才可以將邊端力優化到最小。由前文分析可知,邊端力是以極距為最小的周期函數,因此在一個極距范圍內,基波占的比重應該最大。則式(7):
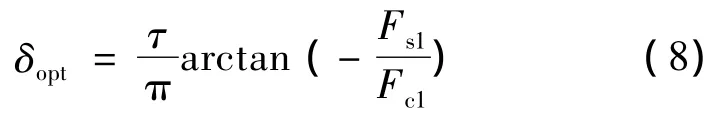
由于實際操作中不能使初級鐵心的長度為無限長,因此只要使鐵心的另外一端超出次極永磁鐵作用的磁場范圍即可。本文在Ansoft軟件中建立電機單端受力模型,如圖4所示,模型中電機次極保持不動,初級鐵心以每步0.1 mm的步距從左向右運動,運動距離為40 mm。對上述模型進行瞬態分析,得到左右邊端受力曲線如圖5所示。
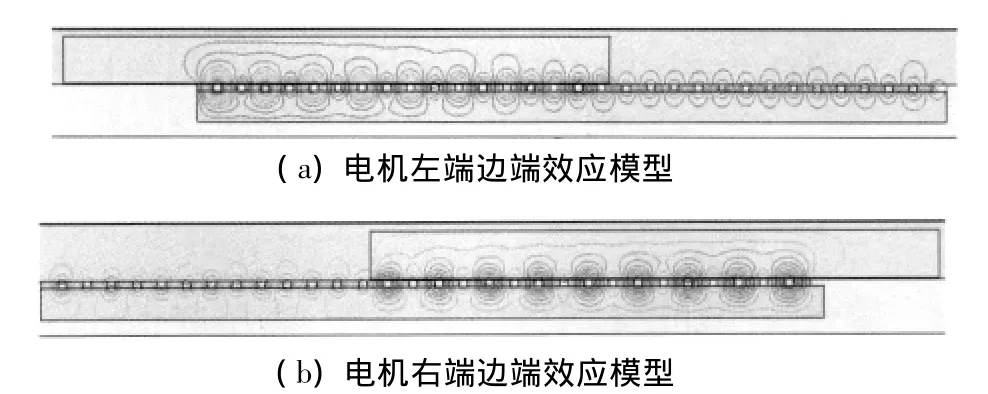
圖4 電機單端邊端效應模型
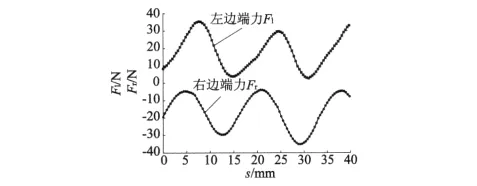
圖5 電機左右邊端受力曲線
從圖5中可以看出,左邊端力始終為正,右邊端力始終為負,且都是極距的周期函數。這和前文的分析結果相一致。對圖5中的左邊端力進行諧波分析,得到基波的正弦和余弦系數分別為508.36和463.66,由式(8)可得使邊端力最小的優化值δ:
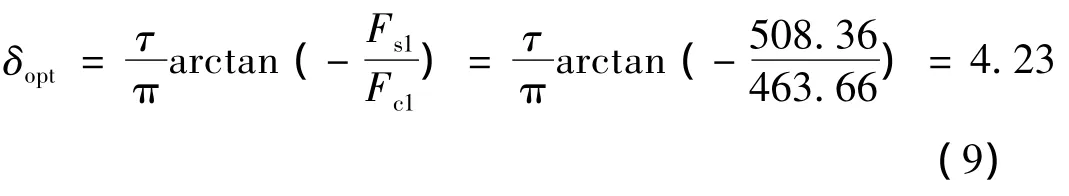
因此優化后的初級鐵心長度:
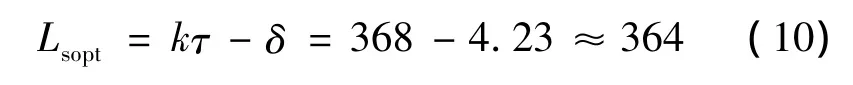
將圖3中模型初級鐵心的長度改為364 mm,在Ansoft軟件中分別對優化前和對優化后的模型進行邊端力分析,得到的邊端力如圖6所示。從結果中可以看出,優化前的邊端力主要由一次諧波構成。優化后的邊端力不存在一次諧波,邊端力的幅值減小到原來的1/3。
由以上仿真結果可以得出,通過對電機初級鐵心單端力進行諧波分析,優化鐵心長度,可以明顯減小邊端力的幅值,進而減小電機的力矩波動。
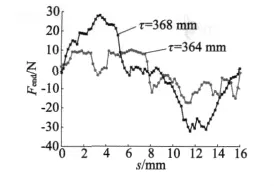
圖6 優化初級長度前后邊端力對比
1.2 永磁同步直線電動機齒槽力分析及優化
降低電機的齒槽力矩的方法有很多,主要有:采用無槽鐵心結構[9],鐵心斜槽或永磁體斜極[10],采用半開口槽或減小齒槽開口大小。以上方法雖然可以很大程度上減小齒槽力矩,但是電機的氣隙磁密也會隨之下降,從而降低電機的推力密度,同時由于齒槽結構變得復雜,加工成本也會隨之增加。本文在不增加電機加工難度的基礎上采用一種分數槽結構來降低電機的齒槽力。
一臺電機總的齒槽力矩可以理解為多個單元齒槽力矩的疊加。以單元槽口中心為零點,當磁極極間中線處在零點位置,它們產生的磁阻力矩為零,當轉子移開,磁極極間中線偏移零點位置時,由于磁阻變化產生了磁阻力矩,力矩有將轉子拉回平衡位置的趨勢。一臺槽數為Z、極數為2p的電機總齒槽力矩可以理解為對于每個槽口,面對2p個磁極極間產生的單元齒槽力矩的疊加,然后是Z個槽口齒槽轉矩的疊加。
由旋轉電機理論可知,轉子轉過一圈出現的基波齒槽轉矩周期等于定子槽數Z和極數2p的最小公倍數。即齒槽轉矩的周期γ:
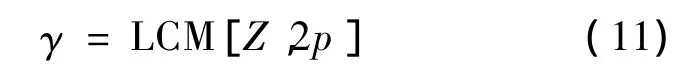
當初極齒槽數Z一定時,通過改變槽距的寬度可以改變次極磁鋼數,從而提高槽數與磁鋼數的最小公倍數,達到提高齒槽力的基波頻率的目的。由頻率函數特性可知,齒槽力基波幅值隨其基波頻率增加而減小,這樣通過提高齒槽力的基波頻率就可以減小其幅值。
直線電動機可以認為是旋轉電機沿徑向剖開,然后將電機的圓周展成直線形成的。那么適合旋轉電機的理論也一定適合直線電動機。不過這里的2p不是指次極永磁體總極數,而應該是初級齒槽結構的有效長度內對應的永磁體極數。由表1可知,優化前電機的槽距為14 mm,槽數為24,極距為16 mm,那么在齒槽結構有效長度范圍內對應的永磁體極數2p為21,對應的齒槽轉矩的周期γ:
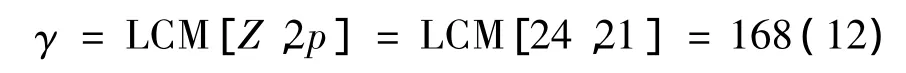
將電機的槽距修改為15 mm,槽數保持不變,為24槽,極距保持不變,為16 mm,那么在齒槽結構有效長度范圍內對應的永磁體極數2p為45/2極,對應的齒槽轉矩的周期γ為:
與邊端力分析思路相同,要想分析齒槽力的大小,必須先排除邊端力對力矩波動造成的影響,本文采用對初級鐵心和次極加周期邊界條件的方式來消除邊端效應對分析結果的影響。建立電機的齒槽效應分析模型如圖7所示。
對槽距為14 mm和15 mm兩種情況的齒槽力模型進行有限元分析,得到齒槽力如圖8所示。
從分析結果可以看出,將槽距從14 mm改為15 mm后,齒槽力的頻率明顯比原來高,但是對應的齒槽力幅值卻從4.1 N降低到1.3 N。仿真結果證明通過改變槽距可以提高齒槽數和永磁體極數的最小公倍數,提高齒槽力的頻率,從而達到降低齒槽力的目的。
2 結 語
本文對雙邊永磁同步直線電動機進行了有限元建模,對造成力矩波動的邊端力和齒槽力形成的原因進行了分析,并采用有限元分析方法對邊端力模型和齒槽力模型分別進行分析,通過優化電機自身結構來減小邊端力和齒槽力,優化效果明顯。由優化結果得到較低力矩波動可以滿足電機定位精度的要求,保證電機正常運行。
[1]Krebs G,Tounzi A,Pauwels B,et al.Modeling of a linear and rotary permanent magnet actuator[J].IEEE Transactions on Magnetics,2008,44(11):4357 -4360.
[2]Lim K C,Woo J K,Kang G H,et al.Detent force minimization techniques in permanent magnet linear synchronous motors[J].IEEE Transactions on Magnetics,2002,38(2):1157 -1160.
[3]Tao Sun,Ji Min Kim,Geun Ho Lee,et al.Effect of pole and slot combination on noise and vibration in permanent magnet synchronous motor[J].IEEE Transactions on Magnetics,20011,47(5):1038-1041.
[4]Inoue M,Sato K.An approach to a suitable stator length for minimizing the detent force of permanent magnet linear synchronous motors[J].IEEE Transactions on Magnetics,2000,36(4):1890-1893.
[5]Zhu Z O,Xia Z P,Howe D,etal.Reductions of cogging force in slot less linear permanent magnet motors[J].IEEE Electric Power Applications,1997,144(4):277 -282.
[6]Hwang S M,Eom J B,Jung Y H,et al.Various design techniques to reduce cogging torque by controlling energy variation in permanent motors[J].IEEE Transactions on Magnetics,2001,37(11):2806-2809.
[7]Yu Wu Zhu,Dae Hyun Koo,Yun Hyun Cho.Detent force minimization of permanent magnet linear synchronous motor by means of two different methods[J].IEEE Transactions on Magnetics,2008,44(11):4345-4348.
[8]Yu Wu Zhu,Sang Gun Lee,Koon Seok Chung,et al.Investigation of auxiliary poles design criteria on reduction of end effect of detent force for PMLSM[J].IEEE Transactions on Magnetics,2008,45(6):2863-2866.
[9]羅宏浩,吳峻,常文森.動磁式永磁無刷直流直線電機的齒槽力最小化[J].中國電機工程學報,2007,27(6):12 -16.
[10]Luo Honghao,Wu Jun,Chang Wensen.Minimization of thrust fluctuation in moving magnet permanent magnet brushless linear DC motors[J].IEEE Transactions on Magnetics,2007,43(5):1968-1972.

