無線傳感器網絡中d-Hop 2-連通容錯支配集的分布式構造算法*

鄭 嬋，尹 令，孫世新

(1.電子科技大學計算機學院，成都610054;2.華南農業大學信息學院，廣州510642)

無線傳感器網絡是由大量具有感知、數據處理和通信能力的傳感器節點組成的網絡，具有低功耗、低成本、智能化、分布式、自組織等特點，在軍事、環保、醫療、商業、農業、災害預測及救援等領域都有著廣闊的應用前景。由于沒有類似蜂窩通信中基站的骨干基礎，且受到傳感器無線收發裝置傳輸半徑和節點能量的限制，多數的節點之間都不能直接進行通信，只能通過若干中間節點形成的虛擬骨干網進行多跳交換數據和通信。在無線傳感器網絡中構造虛擬骨干網是優化網絡結構的一個重要手段，而構建虛擬骨干網最常用的技術就是計算網絡的連通支配集CDS(Connected Dominating Set)。CDS中的支配節點構成高一級的骨干節點控制著全網的路由、維護和管理。在單位圓盤圖UDG(Unit Disk Graph)的網絡模型中構造最小連通支配集MCDS(Minimum CDS)早已被證明是NP完全問題［1］，在節點具有中等規模以上(一般節點數量大于40)時，只能構造近似的最小連通支配集。近十年來，關于構造最小連通支配集已經有較為深入而成熟的研究，研究學者們提出了各種算法來構造近似的最小連通支配集［2］。

隨著無線傳感器網絡規模的增大和密集程度的增加，采用近似的最小連通支配集算法獲得的支配集節點數目依然較大。為了解決這一問題，很多學者［3-8］提出d-hop連通支配集(d-hop CDS)來大大減少支配集節點數量。d-hop CDS指的是受支配節點和支配節點之間的跳數最多可達d跳。當d≥2時，d-hop CDS具有比CDS少得多的支配節點數，可提高網絡容量和網絡性能，因為d-hop CDS將無線傳感器網絡劃分為更大的簇(Cluster)，整個網絡收縮為以d-hop簇頭(Clusterhead)為超級節點的多層次網絡，簇內其余節點都通過d-hop簇頭和別的節點通信。Nguyen等［9］證明了在 UDG中尋找最小 dhop CDS依然是NP完全問題。

另一方面，由于傳感器節點存在能量、存儲和計算等資源約束，節點的失效、鏈路的斷裂會導致網絡失敗，因此構造容錯性好、可靠性高的虛擬骨干網是一個非常有意義的課題。構造具有一定冗余度的k-連通支配集來充當虛擬骨干網可提高網絡的容錯性和可靠性。k-連通指虛擬骨干網中任意k-1個骨干節點出錯，虛擬骨干網仍然是連通的。當k較小(k=2，3等)，k-連通骨干網相對簡單并且具有容錯能力，可在少量節點失效的情況下依然能夠保持骨干網的拓撲連通。

基于上述兩個目的需構建一個既精簡又具有容錯能力的連通支配集作為虛擬骨干網，可結合連通支配集的多跳性質和k-連通性質。

近十年來，關于1-hop的MCDS的構造研究已經較為成熟而深入，提出了多種分布式算法來構造近似的最小連通支配集，其中以基于貪心［10］、Steiner tree［11］、剪枝［12］、最大獨立集［13］、多點中繼集［14］和簇構造［15］等一系列方法的研究為最多。而后從單跳MCDS向d-hop CDS擴展，比較有代表性的是基于簇構造［3-4］、基于貪心［16］、基于剪枝［5-6］的d-hop CDS構造法，以及能量均衡的 CDS構造［17］。Gao等人［7］提出在 UDG 或 UBG(Unit Ball Graph)圖中構造d-hop CDS的多項式近似算法并給出了詳盡的證明。在文獻［3］和文獻［4］中，采用基于Cluster構造來構造d-hop CDS，通信代價和算法時間都依賴于跳數d和節點平均度。Yang等［5］提出了不同一般做法的剪枝策略，初始i=0時所有節點都是ihop CDS，而后對 i=0，1，…d-1 需經過 d次刪減，每次刪減i-hop CDS被剪枝成為(i+1)-hop CDS。文獻［8］更有新意的從青蟲產卵中得到啟示，模擬生物行為構建d-hop CDS，使算法性能能獨立于跳數d和節點平均度，此法適合大規模和超大規模的傳感器網絡的d-hop CDS的構建。

在提高連通支配集的容錯性可靠性方面，學者們也做了許多研究［18-24］，這其中大部分都結合了 k-Vertex連通性和m-支配性。Dai等［18］采用基于概率的、確定的和混合的3種方法構造k-連通k-支配集，文獻［19］也提出k-連通m-支配集的構造法。關于2-連通多支配集也有特定研究［20-21］，Wang等［22］專門研究了2-連通的骨干網構造方法，同時Li等［23］提出兩種中心式的構造2-連通d-hop支配集的方法。據筆者所知，目前研究2-連通d-hop支配集的分布式構造方法鮮少，本文基于單位圓盤圖網絡模型提出d-hop 2-連通支配集的分布式構造算法，d-hop 2-CDS算法(d-hop 2-Connected Domination Set Construction)，主要策略分多步構造，先分簇構造d-hop獨立支配集，后添加路徑節點形成2-連通支配集。

1 問題定義

1.1 定義1 單位圓盤圖UDG(Unit Disk Graph)

一般地，無線傳感器網絡可以抽象為無向單位圓盤圖，網絡中每個傳感器節點在圖中可用單位圓盤中的頂點來表示，如果兩個傳感器節點能相互直接通信則在圖中對應為一條邊。為便于描述，以下將單位圓盤圖簡稱為G=(V，E)。V和E分別表示節點集和邊集。這里只考慮連通的單位圓盤圖G。

1.2 定義2 連通支配集CDS(Connected Dominating Set)

圖 G=(V，E)中，設D?V，?u∈V，u∈D 或 u 與 D中某一節點相鄰，稱D為圖G的支配集(Dominating Set，DS)，DS中的節點稱為支配節點，不在該集中的節點則被稱為受支配節點。若由D導出的子圖為連通圖，則稱D為CDS。若?u∈D，D-{u}不是一個連通支配集，則稱D為圖G的極小連通支配集(MCDS)。

1.3 定義3 極大獨立集MIS(Maximal Independent Set)

圖 G=(V，E)中，設 U?V，若對?u，v∈U，(u，v)?E，即點集中任意2個節點不相鄰，則稱U為圖G的獨立集。若對?u∈V-U，U∪{u}不是一個獨立集，則稱U為圖G的極大獨立集(MIS)。

1.4 定義 4 d-hop CDS［9］

圖 G=(V，E)中，頂點子集 D?V，對?u∈D，v?D，可以找到一條從u到v跳數為d的一條通路(或者說節點u和v之間有d-1個中間節點)，而且由子集D導出的子圖是連通的，則稱頂點子集D為d-hop CDS。特別地，當d=1時，1-hop CDS就是一般意義的CDS。

1.5 定義 5 d-hop 2-連通支配集［22-23］

圖G=(V，E)中，頂點子集D?V，若滿足①D為d-hop CDS;②由子集D導出的子圖是2-連通的，即子集D任意一對頂點間都存在至少2條點不相同的路徑，則稱頂點子集D為d-hop 2-CDS。

1.6 定義6 割點、塊、葉子塊和塊-割點圖

連通圖G中，若移去某個頂點u導致圖G不連通，則u稱為割點(Cut-Vertices)。圖G的不含割點的最大連通子圖稱為塊(block)。圖G的僅含一個割點的連通子圖稱為葉子塊(Leaf Block)。割點示例如圖1所示。明顯地，至少含有3個頂點的塊是2-連通圖。

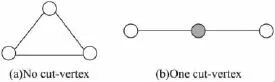
圖1 割點的示例圖

塊-割點圖是個二部圖H，其中一個部集由G的割點構成，另一部集每個點bi對應于G的一個塊Bi，vbi作為H的一條邊當且僅當v∈bi。

2 算法描述

本文總體上分3個步驟分布式構造d-hop 2-CDS:

第1步 每個節點給周圍d-hop鄰居泛洪Hello消息，建立d-hop鄰居發現，收集d-hop范圍的鄰居節點狀態信息。根據收集的信息確定自己著色狀態，所有節點確認完畢即建立d-hop支配集，即d-hop DS。

第2步 從一個支配節點出發，在(d+1)跳范圍內和另一個支配節點之間尋找最短路徑，路徑上的節點作為支配節點的連接點。每個支配節點重復這一過程，直至整個支配集連通。

第3步 對連通支配集導出的塊-割點圖，若存在葉子塊，在葉子塊和其余塊之間尋找最短路徑，并將路徑節點擴充入連通支配集中。重復這一過程，直至塊的個數為1。

2.1 d-hop 鄰居發現

每個節點要發現周圍d-hop鄰居信息，就要先向周圍d-hop范圍的鄰居節點發送泛洪的Hello消息。泛洪的過程如下:

(1)每個節點在首輪信息交換時，向所有一跳鄰居發送Hello消息。收到消息的節點將一跳鄰居保存在本節點的鄰居列表NList中，直至該節點從所有一跳鄰居處都收到Hello消息。

(2)在第 i∈［2，d］輪的信息交換時，每個節點在廣播Hello消息捎帶(i-1)hop鄰居列表信息。

(3)經過(1)和(2)共d輪的消息交換每個節點都可以匯集周圍d-hop范圍的鄰居節點狀態信息(包括鄰居的ID和著色狀態等信息)，這些鄰居信息都保存在該節點的鄰居列表NList中。

2.2 第1步 構造d-hop MIS

節點用3種顏色(黑色、灰色和白色)來分別代表3種狀態。

(1)支配節點(黑色):支配集的成員

(2)受支配節點(灰色):被支配節點支配的節點

(3)未定狀態(白色):指空閑或初始的狀態

節點的狀態變化基于以下原則:

原則1 未定狀態(白色)→受支配節點狀態(灰色):如果一個白色節點收到一條來自于黑色節點v的消息，該白色節點將自己變為灰色，并成為支配節點v的受支配節點。

原則2 未定狀態(白色)→支配節點狀態(黑色):如果一個白色節點發現在它及它周圍d-hop的所有白色節點中，自己擁有最大ID，且這一結果狀態維持一個時間Iτ。該白色節點將自己變為黑色。

將d-hop 2-CDS算法的第1步具體過程歸納如下:

算法1:構造d-hop簇，所有簇頭構成d-hop MIS

(1)計算并發現所有節點的d-hop鄰居，每個節點將鄰居信息(包括鄰居ID和著色狀態等)保存在本節點鄰居列表中;

(2)初始時所有節點都為白色。選擇所有d-hop白色鄰居中有最大ID的白色節點，將它變為黑色，和該黑色節點相鄰的所有d-hop白色鄰居們皆標為灰色。將此黑色節點加入支配節點集合D。在這一輪著色中，黑色和灰色構成了d-hop Cluster，簇節點加入集合C，黑色節點為Clusterhead;

(3)考慮點集合C的所有一跳鄰域中，計算并發現擁有最大ID的白色節點，將之著黑色，同時將被黑色節點支配的節點都著灰色。黑色節點繼續加入支配節點集合D，黑色和灰色也加入集合C。如此不斷擴充支配節點D和簇節點集合C，直至C為全頂點集合V或者說找不到白色節點為止;

(4)返回獨立的支配節點集合D作為d-hop Dominating Set。算法1完畢。

2.3 第2步 構造d-hop連通支配集

構造d-hop連通支配集的過程就是將算法1得到的d-hop DS中的支配節點尋找連接節點(Connector)連接起來。支配節點和連接節點共同構成了 d-hop的 CDS。

每個黑色簇頭管理和維護著一個本地表T，表T用來記錄到達另一個黑色簇頭的路徑。如果一個黑色簇頭v收到另一個簇頭w發來的INVITE消息，若w沒有在表T中，這時將w和INVITE。PathList加入表T中。否則，若表T中已經含有w，但是由消息IN-VITE。PathList獲知的v和w之間的新路徑比表T中的老路徑更短，則用更短的新路徑替換老路徑。消息的PathList中的節點是連接節點Connector。

算法2:將d-hop獨立支配集連通起來

(1)每個黑色簇頭節點向周圍(d+1)-hop廣播INVITE消息，消息中包含路徑列表PathList;

(2)從某個指定簇頭根節點開始，根據簇頭本地表T來構建局部最小生成樹，僅向其具有最大 ID的兒子廣播DISTANCE消息(消息中包含父親簇頭生成的局部最小生成樹節點)，當兒子簇頭節點收到DISTANCE消息，繼續擴充最小生成樹(須避免和父親節點形成環路)，向具有最大ID的孫子廣播，這一過程直至DISTANCE消息傳遍全網的簇頭節點并已無法擴充最小生成樹為止。此時所有簇頭節點位于最小生成樹頂點，而連接點位于最小生成樹路徑上;

(3)獲得的連接點加入d-hop CDS集合D中，返回集合D。算法2完畢。

2.4 第3步 擴充d-hop 2-連通支配集

由算法的前兩步獲得的d-hop連通支配集為D。第3步對D導出的塊-割點圖G［D］只要存在葉子塊L，尋找將L和D-L連接的路徑P，P須滿足:(1)該路徑兩端點是L和D-L中，路徑的中間節點必須是原始網路圖G中非D集合的節點;(2)該路徑是最短的，即中間節點個數最少的路徑。

這里假設前3步獲得的d-hop連通支配集D導出塊-割點圖為G［D］，對G［D］塊的個數記為B［D］，路徑P的中間節點集合為I。

算法3 繼續擴充路徑，將d-hop支配集2-連通

(1)采用Depth First Search(DFS)法對 G［D］計算塊個數 B［D］;

(2)若B［D］＞1，計算葉子塊和G［D］中其余部分的最短路徑P，P的中間節點不屬于D，將P中間節點集合I擴充入D，即 D=D∪I;

(3)重新計算 B［D］，重復執行上述2)過程，直至 B［D］=1。返回集合D。算法3完畢。

2.5 d-hop 2-CDS算法實例展示

在100×100的矩形區域內，隨機放置100個傳感器節點，每個節點通信半徑為15。對d=2，3和4，本文算法前兩步獲得2-hop，3-hop和4-hop CDS分別如圖2(a)、2(b)和2(c)所示。這里d-hop CDS被連通為樹狀。

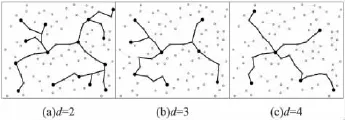
圖2 生成的d-hop CDS示例圖

初始UDG網絡圖如圖3(a)所示。以d=3為例，運行算法的第1和第2步驟可生成3-hop CDS，如圖3(b)和3(c)所示。運行第3步可生成3-hop 2-CDS，如圖3(d)所示。

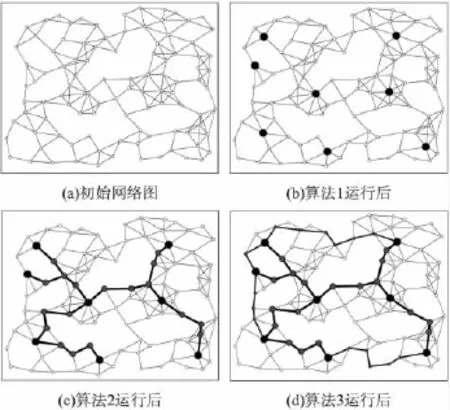
圖3 d-hop 2-CDS算法在各階段后實例場景圖(以d=3為例)

3 性能評價

3.1 算法理論分析

定理1 本文d-hop 2-CDS算法時間復雜度為O(d(mn+n2))，其中d為跳數，m為網絡圖邊數，n為網絡節點個數;消息復雜度為O(d2Δ(mn+n2))，其中Δ為最大節點度。

證明 事實上此算法時間最大消耗在第3步。(1)先考慮算法的前2步構造時間，含有 d-hop或(d+1)-hop的泛洪步驟，雖每個節點的泛洪消息是并行的，但由于消息跳數為d或(d+1)，因此發送消息的時間和d成正比。另外，構造時間也和網絡節點數量n成正比，這由于在算法第1步(§3.2)每個節點須確定自己的著色狀態，算法第2步(§3.3)每個距離為(d+1)的支配節點互連，這兩個過程都類似:連續而非并行。最壞時間復雜度發生在當所有節點以優先級鏈狀遞增排列或遞減排列時，節點最大的節點度為2。此時，每個節點都必須在等所有具有較大優先級的節點確定之后才能確認自己。因此，算法的前兩步時間復雜度為O(dn)，其中d為跳數，n為網絡節點個數。

(2)在算法第3步，深度優先搜索(DFS)塊個數的計算需O(m+n)，m為網絡圖邊數。每次循環中最短路徑計算需O((2d+1)×n)，因為所擴充的2-連通路徑長度不超過(2d+1)。因此算法第3步需O((m+n)(2d+1)n)，可簡化為 O(d(mn+n2))，綜合(1)(2)得證。

另外，關于算法的消息數量的分析，每個節點d-hop泛洪消息的數量是和跳數d的平方成比例關系;節點個數n和總泛洪消息數量成正比;不考慮丟包等通信損失，每個節點都的和周圍所有鄰接點交換消息，因此消息代價還和平均節點度成正比關系。綜上前述(1)(2)的循環次數分析，算法的消息復雜度為O(d2Δ(mn+n2))，其中Δ為最大節點度。

引理 1［24］UDG 圖 G=(V，E)中，定義 I為r-hop IS，對G中任意一頂點 u，|Nr(u)∩I|≤β，其中:

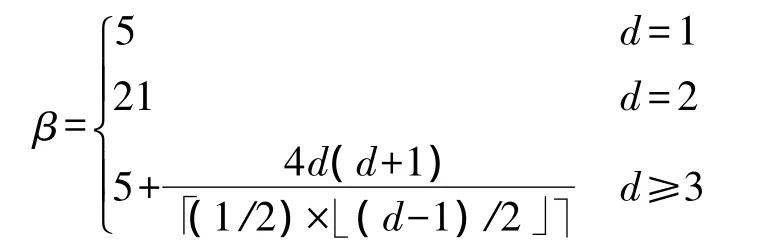
引理2 算法第2步，連通節點使得所有獨立支配節點連通而形成生成樹的頂點，這樣插入的連接節點個數不超過d(|I|-1)，d為跳數，I同引理1定義。

證明 算法第2步，將第1步生成的|I|個節點組織成生成樹，樹的頂點就是支配節點，而樹的路徑就是連接節點。樹的路徑個數為|I|-1，由于是最短路徑每條路徑長度不超過d，因此，插入的連接節點個數不超過d(|I|-1)。

引理3［23］算法第3步，插入連通節點使得算法第2步已連通的d-hop CDS能具有2-Connect性質，每次循環計算塊個數后插入的路徑節點個數不超過2β+2d，d為跳數，β同引理1定義。

引理1和引理3證明略，參閱文獻［23-24］。

定理2 本文d-hop 2-CDS算法是一個(2β+2d+1)(d+1)β的近似算法，這里d為跳數，β同引理1定義。

證明 令|MCDS|表示G中最小連通支配集內頂點的個數，OPT(G)表示最優d-hop 2-連通支配集中頂點的個數，顯然，d-hop 2-連通支配集也是CDS，D，I，D2和D3分別是本算法輸出的d-hop 2-連通支配集，本算法第1步產生的d-hop IS，第2步添加的連接點集合以及第3步再次添加的使2-連通的連接點集合。其中第3步循環次數(即塊的個數)最多|I|+|D2|-1次，則由引理1至引理3，有:

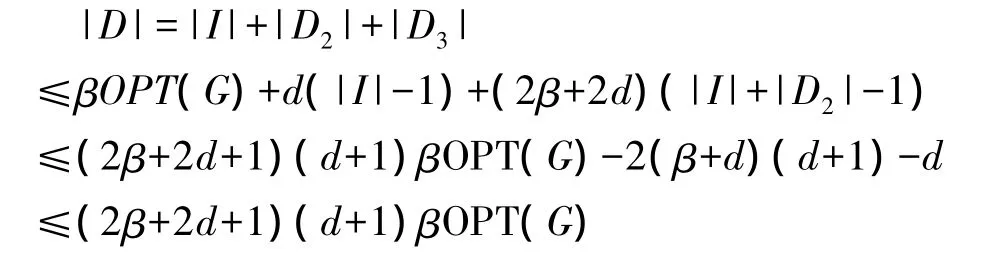
所以，本算法的近似比為:

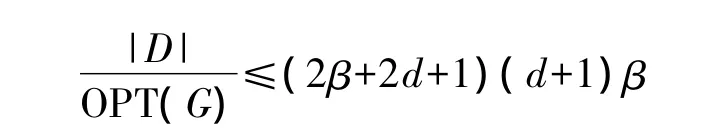
3.2 算法仿真分析

仿真環境1:100×100的矩形區域，傳感器節點隨機布置，通信半徑 r=15時，本文算法產生的 d-hop獨立支配集和2-連通支配集(d=1，2，3，4)隨節點個數 n(n=80，100，150，200，250，300)的變化關系如圖4(a)和4(b)所示。從圖中可得:隨著d的增大，支配集或連通支配集的大小急劇縮小，即可選取更少的節點作為虛擬骨干網以支配其余節點，這驗證了支配集的d-hop性質可以大大減小支配集節點數目。另外，隨著節點個數n的增大，d-hop DS緩慢增加，這是由于節點密度雖增加，原本的支配節點依然可支配新增加的大多數節點。

圖4 當通信半徑r=15時，隨n的變化關系

仿真環境2:100×100的矩形區域，傳感器節點隨機布置，節點個數n=100時，本文算法產生的d-hop支配集和2-連通支配集(d=1，2，3，4)隨通信半徑 r(r=12，14，15，16，18，20)的變化關系如圖5(a)、5(b)所示。半徑r增大，平均節點度增加，網絡圖也更加密集，支配節點數量下降。說明在密集網絡圖中本算法具有較好性能。

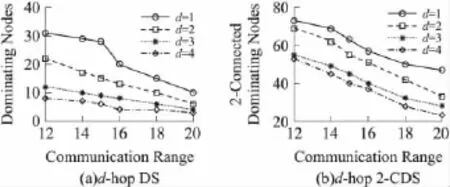
圖5 當n=100，通信半徑為r時，隨r的變化關系

4 結論

本文提出了基于UDG網絡模型的d-hop 2-連通支配集的分布式構造算法。先構造d-hop獨立支配集，然后連通形成 d-hop連通支配集(d-hop CDS)，最后再次擴充路徑形成2-連通集。理論和實驗都表明:d-hop CDS有著比單跳CDS少得多的連通支配節點個數，因而采用d-hop CDS作為虛擬骨干網也就可以大大減少骨干節點的個數，增加了網絡的可擴展性和網絡容量。另外2-連通的性質也可以增加虛擬骨干網容錯性和可靠性。下一階段的研究將著重在節點自由運動模式下d-hop連通支配集的維護代價的探討。

［1］ Garey M R，Johnson D S.Computers and Intractability:A Guide to the Theory of NP-Completeness［M］.New York:W.H.Freeman and Company，1990:71-72.

［2］ Zheng C，Sun S X，Huang T Y.Constructing Distributed Connected Dominating Sets in Wireless Ad Hoc and Sensor Networks［J］.Journal of Software，2011，22(5):1053-1066.

［3］ Yang S H，Wu T，Cao J N.Connected k-Hop Clustering in Ad Hoc Networks［C］//Proceedings of ICPP:2005 International Conference on Parallel Processsing.Oslo，Norway，2005:373-380，649.

［4］ Theoleyre F，Valois F.A Self-Organization Structure for Hybrid Networks［J］.Ad Hoc Networks，2008，6(3):393-407.

［5］ Yang H Y，Lin C H，Tsai M J.Distributed Algorithm for Efficient Construction and Maintenance of Connected k-Hop Dominating Sets in Mobile Ad Hoc Networks［J］.Mobile Computing，2008，7(4):444-457.

［6］ Rieck M，Pai S，Dhar S.Distributed Routing Algorithms for Multi-Hop Ad Hoc Networks Using d-Hop Connected d-Dominating Sets［J］.Computer Networks，2005，47(6):785-799.

［7］ Gao X F，Wang W，Zhang Z，et al.A PTAS for Minimum d-Hop Connected Dominating Set in Growth-Bounded graphs［J］.Optimization Letters，2010，4(3):321-333.

［8］ Janacik P，Kujat A.Biologically-Inspired Construction of Connected k-Hop Dominating Sets in Wireless Sensor Networks［C］//Proceedings of SASO:2009 Third IEEE International Conference on Self-Adaptive and Self-Organizing Systems.San Francisco，California，USA，2009:103-114，294.

［9］ Nguyen T N，Huynh D T.Connected d-Hop Dominating Sets in Mobile Ad Hoc Networks［C］//Proceedings of 2006 4th International Symposium on Modeling and Optimization in Mobile，Ad Hoc and Wireless Networks.2006:138-145，734.

［10］ Das B，Bharghavan V.Routing in Ad-Hoc Networks Using Minimum Connected Dominating Sets［C］//Proceedings of ICC’97:1997 IEEE International Conference on Communications-Towards the Knowledge Millennium.Montreal，1997，1-3:376-380，1743.

［11］ Min M K，Du H W，Jia X H，et al.Improving Construction for Connected Dominating Set With Steiner Tree in Wireless Sensor Networks［J］.Journal of Global Optimization，2006，35(1):111-119.

［12］ Dai F，Wu J.An Extended Localized Algorithm for Connected Dominating Set Formation in Ad Hoc Wireless Networks［J］.IEEE Transactions on Parallel and Distributed Systems，2004，15(10):908-920.

［13］ Alzoubi K M，Wan P J，Frieder O.Message-Optimal Connected Dominating Sets in Mobile Ad Hoc Networks［C］//Proceedings of MOBIHOC.EPFL Lausanne，Switzerland，2002:157-164.

［14］ Adjih C，Jacquet P，Viennot L.Computing Connected Dominated Sets with Multipoint Relays［C］//Proceedings of Ad Hoc ＆ Sensor Wireless Networks(AHSWN)2005:27-39.

［15］ Gerla M，Tsai J T C.Multicluster，Mobile，Multimedia Radio Network［J］.Wireless Networks，1995，1(3):255-265.

［16］ Sausen P S，Spohn M A，Lima A M N，et al.Boundeddistance Multi-Coverage Backbones in Wireless Sensor Networks［C］//Proceedings of SAC:2007 ACM Symposium on Applied Computing.Seoul，Korea，2007:203-208.

［17］付永生，李善平，周波.無線傳感網絡中能量均衡的連通支配集算法［J］.傳感技術學報，2010，23(8):1142-1145.

［18］ Dai F，Wu J.On Constructing k-Connected k-Dominating Set in Wireless Networks［C］//Proceedings of Special Issue 19th International Parallel and Distributed Processing Symposium(IPDPS).2005.

［19］ Wu Y，Li Y.Construction Algorithms for k-Connected m-Dominating Sets in Wireless Sensor Networks［C］//Proceedings of MobiHoc’08 Proceedings of the 9th ACM international Symposium on Mobile Ad Hoc Networking and Computing.New York，2008:83-90.

［20］ Liu Z L，Tian F，Xu J M.Probabilistic Analysis of upper Bounds for 2-Connected Distance k-Dominating Sets in Graphs［J］.Theoretical Computer Science，2009，410(38-40):3804-3813.

［21］ Schleich J，Danoy G，Bouvry P，et al.Blackbone2，an Efficient Deterministic Algorithm for Creating 2-Connected m-Dominating Set-Based Backbones in Ad Hoc Networks［C］//Proceedings of the Seventh Acm International Symposium on Mobility Management and Wireless Access，Mobiwac09，2009:91-98.

［22］ Wang F，Thai M T，Du D Z.On the Construction of 2-Connected Virtual Backbone in Wireless Networks［J］.IEEE Transactions on Wireless Communications，2009，8(3):1230-1237.

［23］ Li X Y，Zhang Z.Two Algorithms for Minimum 2-Connected r-Hop Dominating set［J］.Information Processing Letters，2010，110(22):986-991.

［24］ Zahng Z，Liu Q，Li D.Two Algorithms for Connected r-Hop k-Dominating Set ［J］. Discrete Mathematics， Algorithms and Applications，2009，1(4):485-498.