k階Erlang分布的Pearson-χ2距離

季海波

(宿遷學院教師教育系，江蘇 宿遷 223800)

0 引言

在數理統計中，通常使用Pearson-χ2距離來比較兩個密度函數的差異性。盡管其已經不再滿足距離公理中的某些條件，但是它們確實能夠在某種程度上描述兩個密度函數的差異程度。近年來，人們在討論極值分布的大樣本問題、分布函數的計算機模擬樣本的收斂性時，都將Pearson-χ2距離作為衡量標準來判斷一個密度函數列是否收斂到某個確定的密度函數。

k階Erlang分布是排隊論中常用的一個重要的服務時間分布，它與指數分布有密切的關系。若X1，X2，…，Xk是一列獨立的隨機變量，且都服從指數分布E(μ)，則隨機變量T=X1+X2+…+Xk具有概率密度:

稱T服從參數為μ的k階Erlang分布。

文獻［5］中給出了兩個指數分布之間的Pearson-χ2最大距離。本文著重討論兩個k階Erlang分布的Pearson-χ2距離和Pearson-χ2最大距離，并與兩個指數分布之間的Pearson-χ2距離進行比較。

1 相關定義及引理

定義1 設隨機變量X、Y分別具有密度函數f(x)、g(x)，且f(x)＞0，若

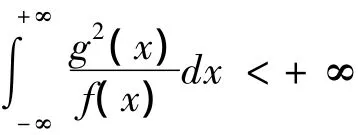
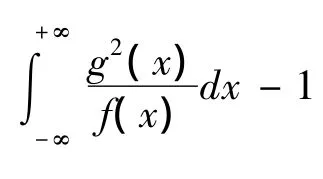
定義2 設隨機變量X、Y分別具有密度函數f(x)、g(x)且f(x)＞0，g(x)＞0，若d2(f，g)、d2(g，f)都存在，記 d2m(f，g)=max{d2(f，g)，d2(g，f)}，稱(f，g)為兩個密度函數f(x)、g(x)之間的最大距離。

由定義可以得到如下引理:

引理1 如果函數f(x)是指數分布E(μ1)的密度函數，g(x)是指數分布E(μ2)的密度函數，那么

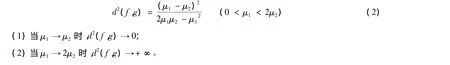
引理2 如果函數f(x)是指數分布E(μ1)的密度函數，g(x)是指數分布E(μ2)的密度函數，當＜μ1＜ 2μ2時，則有:

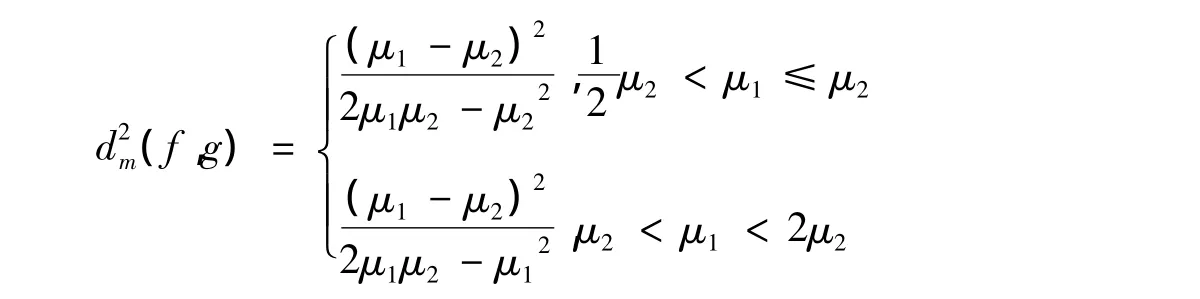
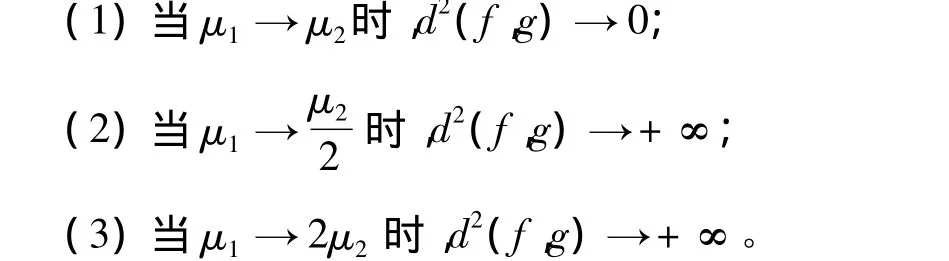
2 k階Erlang分布的Pearson-χ2距離和Pearson-χ2最大距離

定理1 設f(x)、g(x)是分別具有參數μ1、μ2的k階Erlang分布的密度函數，則:

證明:由于f(x)、g(x)是分別具有參數μ1、μ2的k階Erlang分布的密度函數，則:

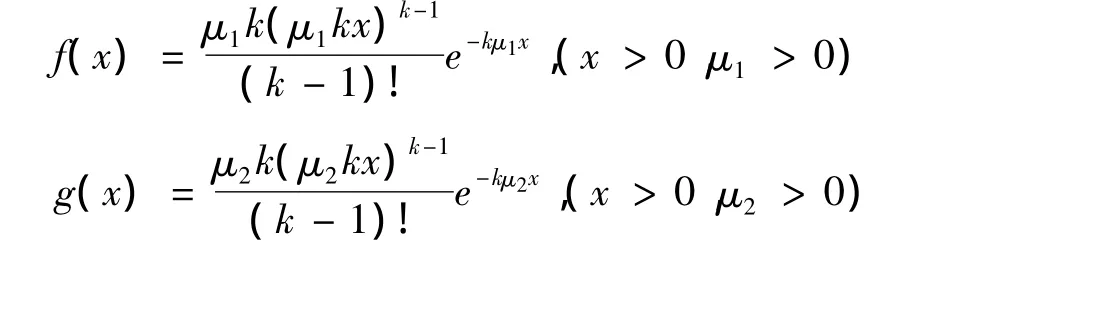
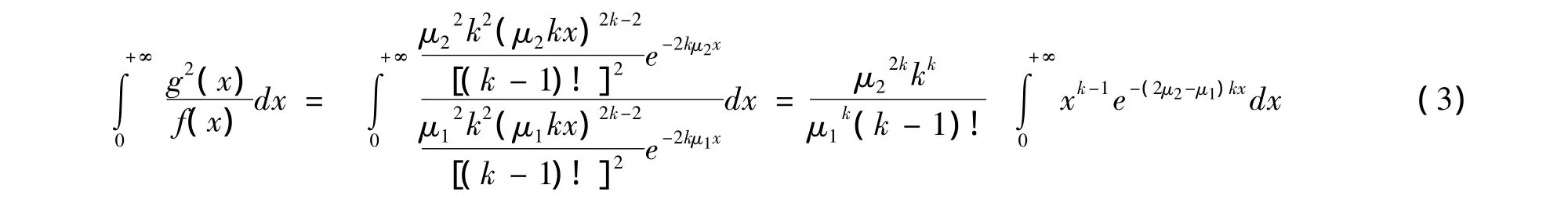
當0＜μ1＜2μ2時，由分部積分法可得:

將式(4)代入式(3)可得:

顯然還有:

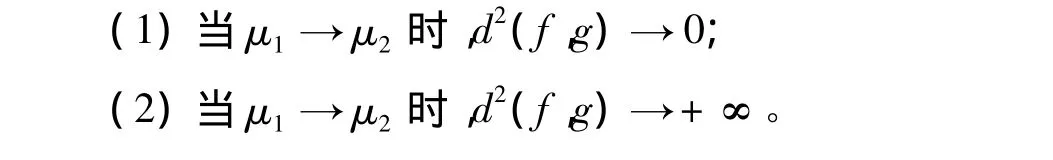
則定理1得證。

類似地還可以得到:

由引理1和定理1還可得到下面一些性質。

推論1 如果f1(x)、g1(x)分別是具有參數μ1、μ2的指數分布的密度函數，f2(x)、g2(x)分別是具有參數μ1、μ2的k階Erlang分布的密度函數，則:

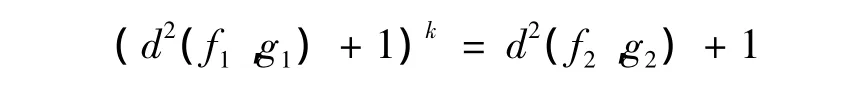
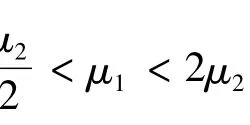
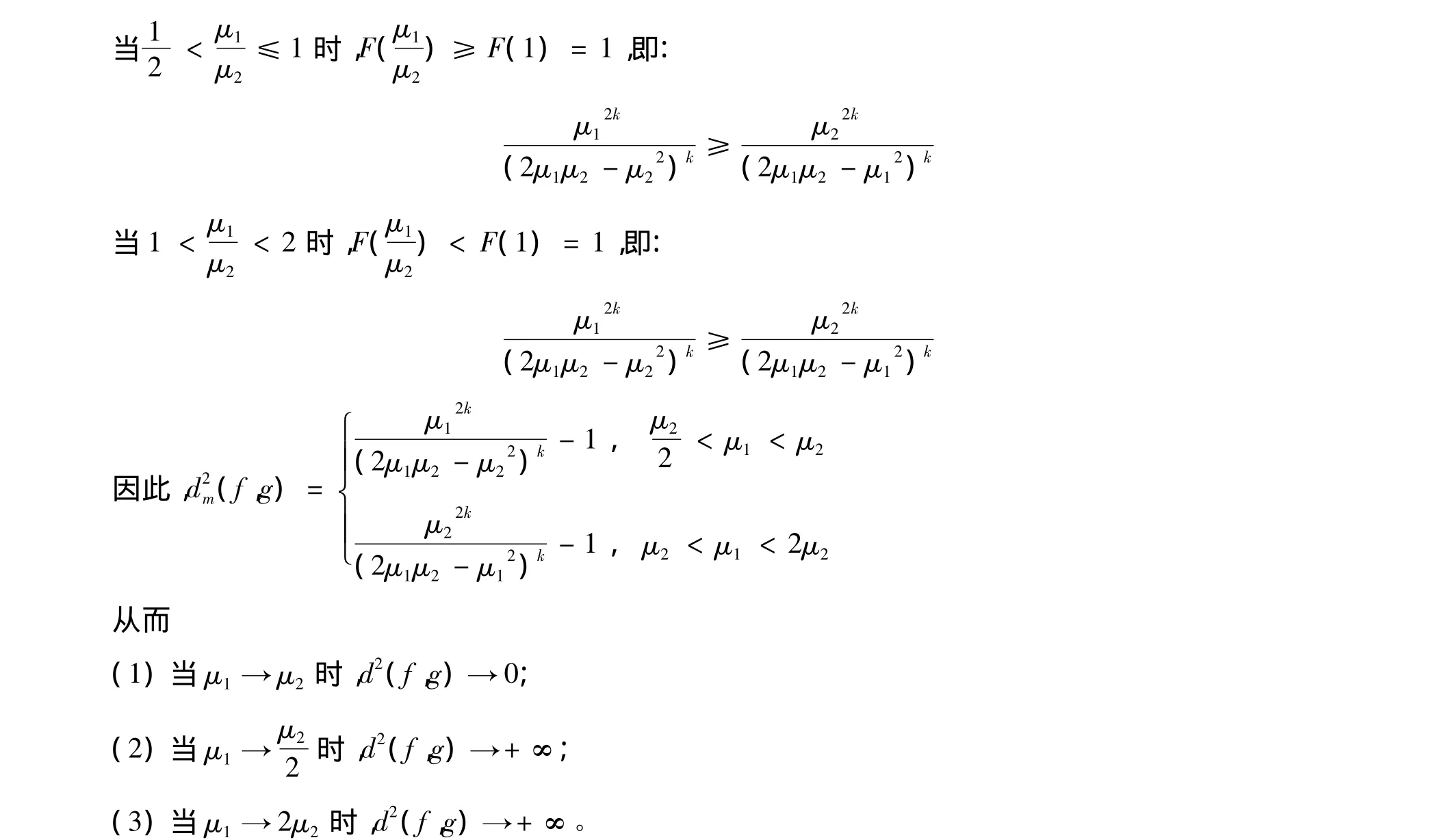
推論2 兩個指數分布間的Pearson-χ2最大距離和兩個k階Erlang分布Pearson-χ2最大距離具有相同的漸近性。

［1］Robert G O，Shau S K.Updating schemes，correlation structure，blocking and parameterization for the Gibbssampler［J］.J R Statist Soc B，1997，59:291-317.

［2］Liu S J，Wong W H，Kong A.Correlation structure and convergence rate of the Gibbs sampler with various scans［J］.J R Statist Soc B，1995，57:157-169.

［3］Reiss R D.Approximate Distributions of Order Statistics［M］.New York:Springer，1980.

［4］胡運權.運籌學基礎及應用［M］.北京:高等教育出版社，1986.

［5］陳光曙.Pearson-χ2的最大距離的性質［J］.遼寧師范大學學報:自然科學版，2005，28(4):402-404.