多粒度空間中的粗糙隸屬度與知識粒度

楊習貝，顏 成，陳 才，於東軍

(1.江蘇科技大學 計算機科學與工程學院，江蘇鎮江 212003;2.南京理工大學計算機科學與技術學院，南京 210094;3.江蘇尚博信息科技有限公司，江蘇無錫 214072)

0 引言

作為粒計算的一種重要數學模型，粗糙集理論在模式識別、知識發現、決策分析、醫療診斷等眾多領域已經取得了很大的進展。

傳統粗糙集及其很多拓展模型是建立在一個二元關系基礎上的，這個二元關系可以是不可分辨關系、相容關系、序關系甚至是沒有任何約束條件的二元關系。根據某個特定二元關系，可以得到論域上的一個劃分或者覆蓋，這個劃分或者覆蓋實際上是一些信息粒的合集，因而可將這個合集視作一個粒空間。從這個角度來看，這些粗糙集方法是在一個粒空間中進行概念的近似逼近，因而是單粒度空間中的粗糙集。

然而，隨著研究的不斷深入以及應用需求的不斷增加，單粒度粗糙集方法在很多數據處理問題上不再適用。例如，在決策分析問題中，多個決策者之間的關系有可能是相互獨立的，因而需要在多個相互獨立的粒空間中進行目標的近似逼近。從這個觀點出發，錢宇華、梁吉業等人提出了多粒度粗糙集的概念。多粒度粗糙集與單粒度粗糙集最本質的區別是可以使用一族而非單個粒空間中的知識來進行概念的近似逼近。

在文獻［5］中，錢宇華、梁吉業等人將由一族等價關系所形成的論域上的一族劃分看作一個多粒度空間，在這個空間中，給出了樂觀多粒度粗糙集模型。與此同時，他們將這種樂觀多粒度粗糙集模型引入不完備信息系統，采用一族容差關系構建多粒度空間。在此基礎上，他們又在由一族劃分所構成的多粒度空間中，給出了悲觀多粒度粗糙集模型。在上述這些工作中，多粒度空間是由一次性給出的一族二元關系得到的，因而可將其視作同步多粒度方法。

為了降低粗糙集理論中知識約簡及規則抽取的算法復雜度，錢宇華、梁吉業等人提出了基于正向近似的通用特征選擇加速算法。這種算法以核屬性集為起點，根據正向近似方法逐次從論域中去掉協調部分的對象。正向近似采用一個使得多粒度空間逐漸細化的偏序關系來表述目標概念，這種方法可被視作異步多粒度方法。

1 多粒度粗糙集模型

令U為一個非空有限論域，R={R1，R2，…，Rm}為論域上一族等價關系的集合，稱二元組(U，R)為一個知識基。

定義1 令(U，R)為一知識基，其中R1，R2…Rm∈R，令R={R1，R…Rm}，對于?X?U，X的樂觀多粒度下近似集合(X)與上近似集合(X)分別定義為:

定義2 令(U，R)為一知識基，其中R1，R2…Rm∈R，令R={R1，R…Rm}，對于?X?U，X的樂觀多粒度下近似集合RP(X)與上近似集合RP(X)分別定義為:

由定義1和定義2可以看出，樂觀多粒度下近似要求至少有一個粒度層次上的等價類包含在目標概念中，而悲觀多粒度下近似則要求所有粒度層次上的等價類都包含在目標概念中，因而悲觀多粒度下近似的要求比樂觀多粒度下近似的要求更嚴格。樂觀多粒度上近似和悲觀多粒度上近似都是根據其下近似的補集來定義的。據此，很容易得到如下性質。

定理1 令(U，R)為一知識基，其中R1，R2…Rm∈R，令R={R1，R…Rm}，對于?X?U，有:

定義3 令(U，R)為一知識基，其中R1，R2…Rm∈R，令R={R1，R…Rm}，則多粒度粗糙隸屬度函數有如下兩種形式的定義:

很明顯，多粒度空間下的粗糙隸屬度依然滿足性質0≤maxμRX(x)≤1，0≤minμRX(x)≤1。

定理2 令(U，R)為一知識基，其中 R1，R2…Rm∈ R，令 R={R1，R…Rm}，有

證明:僅證式(9)，其他證明過程類似。

定理3 令(U，R)為一知識基，其中R1，R2…，Rm∈R，R={R1，R2…Rm}，若R1?R2?…?Rm，則對于?X?U，有:

定理3 在一個多粒度空間中，隨著等價關系的嵌套變化，樂觀多粒度下、上近似集與最粗粒度等價關系所得到的下、上近似是等價的;悲觀多粒度下、上近似集與最細粒度等價關系所得到的下、上近似是等價的。

2 多粒度空間中的知識粒度

2.1 知識粒度的兩種定義方式

令(U，R)為一知識基，其中R1，R2…Rn?R，則每個等價關系族Ri(1≤i≤n)所構成的劃分就組成了一個多粒度空間。形如:

需要注意的是，多粒度空間MSi不是論域上一族子集的合集，而是由m個劃分所構成的合集，所有的等價關系族R1，R2…Rm所構成的劃分就組成了n個多粒度空間。形如:

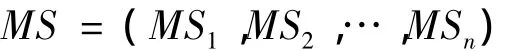
定義4 令(U，R)為一知識基，其中R1，R2…Rm∈R，令R={R1，R2…Rm}，則多粒度空間中的知識粒度有如下兩種形式的定義:

由于本文是基于劃分的多粒度空間進行討論的，所以定義4中的知識粒度有如下等價的形式:

類似于經典粗糙集理論，多粒度空間中的知識粒度也表示了一族等價關系的分辨能力。若知識粒度越大，則表示多粒度空間的分辨能力越弱;若知識粒度越小，則表示多粒度空間的分辨能力越強。當等價關系族R中只有一個等價關系時，多粒度空間中的知識粒度GK∩(R)和GK∪(R)就退化為經典粗糙集理論中知識粒度的定義。根據上述討論，顯然有:

(1)若?Ri∈R使得U/Ri={x:x∈U}，則知識粒度GK∩(R)達到最小值;

(2)若?Ri∈R使得U/Ri={x:x∈U}，則知識粒度GK∪(R)達到最大值;

(3)若?Ri∈R使得U/Ri={U}，則知識粒度GK∩(R)達到最大值 1;(4)若?Ri∈R使得U/Ri={U}，則知識粒度GK∪(R)達到最大值1。

2.2 基于知識粒度的多粒度空間約簡

根據定義4中所示的兩種知識粒度的定義，下面討論如何對多粒度空間進行約簡。多粒度空間的約簡就是在多粒度空間中根據一定的約束條件，刪除一些冗余的粒空間。由于在多粒度空間中，知識粒度有“交”和“并”兩種形式，所以可以分別將這兩種知識粒度作為啟發式函數來對多粒度空間進行約簡。

定義5 令(U，R)為一知識基，其中 R1，R2…Rm∈ R，令 R={R1，R2…Rm}，?R＇? R。

(1)若GK∩(R＇)=GK∩(R)，則稱R＇是R的一個“交”協調集;

(2)若 R＇是R的一個“交”協調集且對于?R＇＇?R＇，R＇＇都不是R的“交”協調集，則稱R＇是R的一個“交”約簡;

(3)若GK∪(R＇)=GK∪(R)，則稱R＇是R的一個“并”協調集;

(4)若 R＇是R的一個“交”協調集且對于?R＇＇?R＇，R＇＇都不是R的“并”協調集，則稱R＇是R的一個“并”約簡。

根據定義5可知，R的“交”約簡是保持多粒度空間中知識粒度GK∩(R)不變的最小等價關系子集;而R的“并”約簡則是保持多粒度空間中知識粒度GK∪(R)不變的最小等價關系子集。這兩種約簡的概念都可以在等價關系族R中約去一些冗余的等價關系，從而簡化由等價關系族R所形成的多粒度空間。

類似于粗糙集理論中的啟發式約簡算法，以下給出定義5中約簡算法的一般步驟。

2.2.1 求多粒度R的一個“交”約簡

輸入:等價關系族R={R1，R2…Rm}，輸出:R的一個“交”約簡R＇。步驟如下:

第1步，令R＇= ?;

第2步，判斷GK∩(R＇)=GK∩(R)是否成立，若成立，轉第6步，否則轉第3步;

第3步，對于 ?Ri∈ R-R＇，計算 GK∩(Ri∪ R＇);

第4步，取一個等價關系 Rj∈ R-R＇滿足 GK∩(Rj∪ R＇)=min{GK∩(Ri):Ri∈ R-R＇};

第5步，令R＇=Rj∪R＇，判斷GK∩(R＇)=GK∩(R)是否成立，若成立，轉第6步，否則轉第3步;

第6步，輸出“交”約簡R＇。

讓我們回到“der Morgenstern ist die Venus”這個句子上來。此處“ist”的確不是傳統意義上的系詞，而是一個類似于“killed”的關系詞，即帶有兩個空位的概念詞，它本身作為質料的一部分構成了對無序的相等關系的表達：“( ) ist ( )”，此時它的前后只能填入專名。

2.2.2 求多粒度R的一個“并”約簡

輸入:等價關系族R={R1，R2…Rm}，輸出:R的一個“并”約簡R＇。

步驟如下:

第1步，令R＇= ?;

第2步，判斷GK∪(R＇)=GK∪(R)是否成立，若成立，轉第6步，否則轉第3步;

第4步，取一個等價關系 Rj∈ R-R＇滿足 GK∪(Rj∪ R＇)=min{GK∪(Ri):Ri∈ R-R＇};

第5步，令R＇=Rj∪R＇，判斷GK∪(R＇)=GK∪(R)是否成立，若成立，轉第6步，否則轉第3步;

第6步，輸出“并”約簡R＇。

上述兩種算法的復雜度是O(m2)，其中m表示等價關系族R中等價關系的數目。

3 結論

本文以多粒度空間為研究對象，針對多粒度粗糙集模型和多粒度空間約簡問題進行了討論，提出了兩種形式的多粒度粗糙隸屬度函數，這兩種多粒度粗糙隸屬度函數是經典粗糙集理論中粗糙隸屬度函數的拓展形式。在多粒度粗糙隸屬度函數的基礎上，重構了樂觀和悲觀多粒度粗糙集。以多粒度空間中多個等價關系的交、和、并為基礎，定義了多粒度空間中兩種知識粒度的度量方式，并以這兩種度量為函數，給出了多粒度空間約簡的概念及啟發式算法。

［1］Z.Pawlak.Rough sets-theoretical aspects of reasoning about data［M］.Netherland:Kluwer Academic Publishers，1991.

［2］Y.H.Qian，J.Y.Liang，Y.Y.Yao，et al.MGRS:a multi-granulation rough set［J］.Information Sciences，2010，180:949-970.

［3］Y.H.Qian，J.Y.Liang，C.Y.Dang.Incomplete multigranulation rough set［J］.IEEE Transactions on Systems，Man and Cybernetics，Part A，2010，20:420-431.

［4］Y.H.Qian，J.Y.Liang，W.Wei.Pessimistic rough decision［J］.Journal of Zhejiang Ocean University:Natural Science，2010，29(5):440-449.

［5］錢宇華.復雜數據的粒化機理與數據建模［D］.太原:山西大學，2011.

［6］Y.H.Qian，J.Y.Liang，W.Pedrycz et al.Positive approximation:An accelerator for attribute reduction in rough set theory［J］.Artificial Intelligence，2010，174(9):597-618.

［7］錢宇華，梁吉業，王鋒.面向非完備決策表的正向近似特征選擇加速算法［J］.計算機學報，2011，34(3):435-443.