自適應(yīng)算法在單軸激光慣導(dǎo)初始對(duì)準(zhǔn)中的應(yīng)用＊

冷傳營(yíng) 劉錫敬

（海軍潛艇學(xué)院 青島 266042）

1 引言

單軸旋轉(zhuǎn)激光慣導(dǎo)系統(tǒng)可抑制陀螺常值漂移和加速度零偏引起的系統(tǒng)誤差，已成為我國(guó)船用慣導(dǎo)系統(tǒng)的主要研究對(duì)象之一［1］。初始對(duì)準(zhǔn)是捷聯(lián)慣導(dǎo)系統(tǒng)進(jìn)行導(dǎo)航的前提，對(duì)準(zhǔn)的精度與速度直接關(guān)系到慣導(dǎo)系統(tǒng)的精度與啟動(dòng)特性。卡爾曼濾波技術(shù)在慣導(dǎo)初始對(duì)準(zhǔn)中應(yīng)用廣泛。但在實(shí)際應(yīng)用中，卡爾曼濾波需要事先知道研究對(duì)象的數(shù)學(xué)模型和噪聲的統(tǒng)計(jì)特性。在不準(zhǔn)確的數(shù)學(xué)模型下進(jìn)行濾波，會(huì)導(dǎo)致很大的估計(jì)誤差，甚至導(dǎo)致發(fā)散。由Sage和Husa提出的極大后驗(yàn)估計(jì)器具有原理簡(jiǎn)單、實(shí)時(shí)性好的特點(diǎn)，在慣性技術(shù)中得到了廣泛的推廣和利用。

2 Sage-Husa自適應(yīng)濾波算法

Sage-Husa自適應(yīng)濾波計(jì)算不斷地利用量測(cè)數(shù)據(jù)估計(jì)和校正噪聲統(tǒng)計(jì)特性與模型參數(shù)，從而保證濾波始終處于正常狀態(tài)，因此該方法特別適用于模型有誤差和對(duì)噪聲統(tǒng)計(jì)特性不明確的系統(tǒng)［2］。

設(shè)系統(tǒng)的狀態(tài)方程為

Wk－1，Vk為互不相關(guān)的白噪聲序列，其方差和均值分別為

Sage-Husa自適應(yīng)卡爾曼濾波算法如下［3］：

在對(duì)單軸旋轉(zhuǎn)激光慣導(dǎo)進(jìn)行初始對(duì)準(zhǔn)時(shí)，系統(tǒng)噪聲一般由慣性器件組合的隨機(jī)誤差引起，比較容易進(jìn)行建模估計(jì)，相反地，量測(cè)噪聲受工作環(huán)境影響很大，不確定性很大，很難確定其統(tǒng)計(jì)特性。因此，實(shí)際的工作中，模型的變化主要由量測(cè)噪聲的不確定性引起，所以在對(duì)系統(tǒng)進(jìn)行自適應(yīng)濾波校正時(shí)，只對(duì)觀測(cè)噪聲方差陣Rk和觀測(cè)噪聲均值rk進(jìn)行估計(jì)，這樣可以減少計(jì)算量，提高數(shù)據(jù)處理速度。

3 系統(tǒng)動(dòng)基座初始對(duì)準(zhǔn)誤差模型

3.1 旋轉(zhuǎn)方案設(shè)計(jì)［4］

導(dǎo)航坐標(biāo)系采用地理坐標(biāo)系——東北天坐標(biāo)系。方案設(shè)計(jì)為正反轉(zhuǎn)停，轉(zhuǎn)動(dòng)方式如圖1所示：先繞oz軸正轉(zhuǎn)180°，停止一段時(shí)間Th；再反轉(zhuǎn)180°，停止Th時(shí)間；接著反轉(zhuǎn)180°，停止 Th時(shí)間；再正轉(zhuǎn)180°，停止一段時(shí)間Th。以上轉(zhuǎn)動(dòng)次序?yàn)橐粋€(gè)周期，之后按上述順序循環(huán)轉(zhuǎn)動(dòng)。

3.2 動(dòng)機(jī)坐初始對(duì)準(zhǔn)狀態(tài)方程

假定3個(gè)陀螺漂移誤差模型相同，均為一階馬爾科夫過(guò)程和白噪聲之和［5］：

其中：

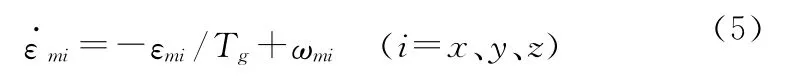
式中：Tg為一階馬爾科夫過(guò)程的相關(guān)時(shí)間；ωmi為激勵(lì)白噪聲。

加速度計(jì)誤差ΔAx、ΔAy主要含有零位偏置ΔAxb、ΔAyb和白噪聲ωAx、ωAy：

將陀螺漂移和加速度零偏擴(kuò)充為狀態(tài)變量，則濾波器的狀態(tài)方程為

式（6）中，狀態(tài)向量和系統(tǒng)噪聲分別為

其中

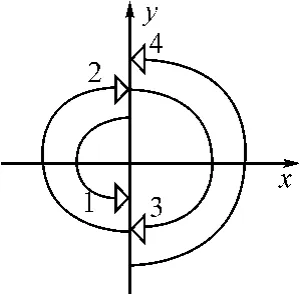
圖1 慣導(dǎo)單軸旋轉(zhuǎn)方案

式中，R 為地球半徑，ωie為地球自轉(zhuǎn)角速度，Cij（i，j＝1、2、3）為捷聯(lián)矩陣中的元素。

3.3 動(dòng)基座初始對(duì)準(zhǔn)量測(cè)方程

選取兩個(gè)位置誤差作為觀測(cè)量，則系統(tǒng)的量測(cè)方程如下：

式中，Z為觀測(cè)向量，Z＝δφ［］δλT；X為系統(tǒng)的狀態(tài)變量；V是系統(tǒng)觀測(cè)噪聲矢量。

4 仿真實(shí)驗(yàn)與分析

設(shè)仿真實(shí)驗(yàn)條件如下：φ取32°，載體速度為Vx＝5m／s、Vy＝0m／s，陀螺漂移為0.003°／h，加速度計(jì)零偏為10－4g，慣導(dǎo)三個(gè)失準(zhǔn)角分別為φx＝10′，φy＝10′，φz＝25′，采樣周期為1s，方位軸旋轉(zhuǎn)角速度為1r／10min，為了驗(yàn)證Sage-Husa自適應(yīng)濾波對(duì)存在較大模型誤差時(shí)的濾波效果，取E（Vk）＝5rk，E（VkVTj）＝100Rkδkj。分別采用kalman濾波算法和自適應(yīng)濾波算法估計(jì)三個(gè)失準(zhǔn)角，均方根誤差曲線如圖2所示。

圖2 三個(gè)失準(zhǔn)角的估計(jì)誤差曲線（1σ）

仿真結(jié)果表明，當(dāng)存在較大模型誤差時(shí)，Sage-Husa自適應(yīng)濾波相對(duì)于傳統(tǒng)kalman濾波的估計(jì)誤差明顯減小，穩(wěn)定性也有了一定的提高。

5 結(jié)語(yǔ)

單軸旋轉(zhuǎn)激光慣導(dǎo)系統(tǒng)動(dòng)基座初始對(duì)準(zhǔn)過(guò)程中，由于環(huán)境的變化，對(duì)噪聲的統(tǒng)計(jì)特性很難確定，會(huì)降低濾波精度，甚至導(dǎo)致濾波發(fā)散，自適應(yīng)濾波算法能夠不斷地對(duì)噪聲統(tǒng)計(jì)特性進(jìn)行實(shí)時(shí)的校正，提高了濾波的精度與穩(wěn)定性。

［1］關(guān)勁，李仔冰.旋轉(zhuǎn)式捷聯(lián)慣導(dǎo)系統(tǒng)精對(duì)準(zhǔn)方法［J］.中國(guó)慣性技術(shù)學(xué)報(bào)，2010，18（4）：396-400.

［2］徐景碩，秦永遠(yuǎn)，彭蓉.自適應(yīng)卡爾曼濾波遺忘因子選取方法研究［J］.系統(tǒng)工程與電子技術(shù)，2004，26（11）：1152-1154.

［3］卞鴻巍，金志華，等.組合導(dǎo)航智能信息融合自適應(yīng)濾波算法分析［J］.系統(tǒng)工程與電子技術(shù)，2004，26：1449-1459.

［4］錢偉行，劉建業(yè)，趙偉，等.基于轉(zhuǎn)動(dòng)基座的SINS初始對(duì)準(zhǔn)方法研究［J］.宇航學(xué)報(bào)，2008，29（3）：928-932.

［5］萬(wàn)德鈞，房建成.慣性導(dǎo)航初始對(duì)準(zhǔn)［M］.東南大學(xué)出版社，1998：36-62.

［6］秦永元.慣性導(dǎo)航［M］.北京：科學(xué)出版社，2006：23-37.

［7］王其，徐曉蘇.旋轉(zhuǎn)IMU在光纖捷聯(lián)航姿系統(tǒng)中的應(yīng)用［J］.中國(guó)慣性技術(shù)學(xué)報(bào)，2007，15（3）：265-268.

［8］王榮穎，許江寧，卞鴻巍.基于可觀測(cè)分析的方位旋轉(zhuǎn)式慣導(dǎo)初始對(duì)準(zhǔn)仿真研究［J］.中國(guó)慣性技術(shù)學(xué)報(bào)，2009，17（1）：15-20.

［9］翁海娜，姚琪，胡小毛.艦船單軸旋轉(zhuǎn)激光捷聯(lián)慣導(dǎo)系統(tǒng)動(dòng)態(tài)初始對(duì)準(zhǔn)［J］.中國(guó)慣性技術(shù)學(xué)報(bào)，2012，20（1）：34-38.

［10］董明杰，汪渤，石永生.旋轉(zhuǎn)－靜止混合對(duì)準(zhǔn)方案在旋轉(zhuǎn)火箭彈中的應(yīng)用［J］.中國(guó)慣性技術(shù)學(xué)報(bào)，2012，20（1）：1-6

［11］朱海，莫君.水下導(dǎo)航信息融合技術(shù)［M］.國(guó)防工業(yè)出版社，2002：079-112.