基于PSOPCNN的圖像濾波算法＊-

柳志忠

（海軍駐葫蘆島431廠軍事代表室 葫蘆島 125004）

1 引言

將粒子群算法（PSO）的基本原理融入到PCNN圖像濾波算法中，從而得到了一種適用于PCNN圖像濾波的粒子群算法，主要考慮PCNN圖像濾波算法的連接系數β、連接系數β及預設閾值V0的參數確定問題，通過粒子群優化算法在解空間里尋求最優解。本文就粒子群算法（PSO）、PSO-PCNN算法、仿真與實驗結果分析等，作進一步的研究和探討［1］。

2 粒子群算法（PSO）

PSO粒子群優化算法（Paritcle Swarm Optimization）具有簡單、較容易實現，具有一定智能化程度，既方便用于科學研究又可用于工程應用等多方面優勢。在PSO算法中過程，搜尋區域中的一個“目標”的過程即是求解每個優化問題的解的過程，這個“目標”被稱為粒子，自己的位置向量和速度向量是每個粒子都具有的特征，每個位置都表示了一組參數值。對于一個D維的優化問題，設一個D維空間中的每一個位置的粒子都代表優化問題中的一個解，而位置就代表著等待被算法優化調整的參數。所有的粒子都有一個適應值（fitness value），被優化的函數決定了該適應值的大小，每個粒子都有一個飛行速度，該速度決定了他們飛翔的方向和距離。然后粒子們就對區域中當前的最優“解”進行搜索［2］。

PSO算法的初始化是對一群隨機粒子隨機的進行的，然后利用迭代的方法尋找最優解。在每一次迭代過程中，粒子通過跟蹤兩個“極值”來對自己進行更新。第一個就是基于粒子自身所找到的最優解，稱為個體極值pi；另一個是整個群體當前所能找到的最優解，稱之為全局極值pg。此外，在局部群體中找到的最優解，稱之為局部極值。

根據對環境的適應度，PSO算法將群體中的個體（粒子）移動到預想的區域，然而該算法不像其他優化算法那樣只優化某個個體，而是把每個個體當作D維搜索空間中的一個無質量、無體積的點（粒子），以一定的速度在D維空間中飛行。然后分別根據它自身和同伴的運動經驗來動態調整飛行速度。

粒子群算法采用以下的數學描述進行定義：假設在一個D維的目標搜索空間中，有一個粒子群是由N個代表潛在問題解的粒子組成的，用一個D維的向量表示其中第i個粒子。飛行速度是vi＝［vi1，vi2，…，viD］T；在D 維的搜索空間中第i個粒子的位置是xi，xi＝［xi1，xi2，…，xiD］T，i＝1，2，…，N；第i個粒子當前搜索到的個體最優位置記為pi，pi＝［pi1，pi2，…，piD］T；粒子群當前搜索到的全局最優位置記為pg，pg＝［pg1，p2，…，pgD］T。PSO 算法對粒子的操作采用下列公式進行：

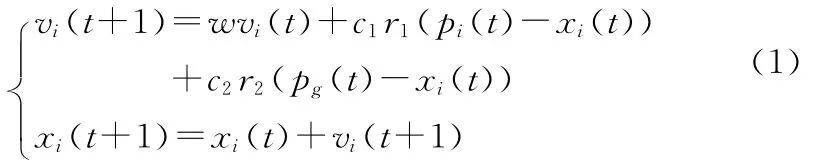
式中，i＝1，2，…，N；t為迭代代數；w 為加權因子，取值在0.1～0.9之間；c1，c2為學習因子，一般取值為2；r1，r2是對角線元素是在［0，1］之間均勻分布的隨機數組成的D×D維的對角線矩陣。為了把vi（k）和xi（k）的值控制在合理的區域內，有必要用參數進行限制。式（1）可以決定粒子下一步的運動速度和粒子坐標。這樣的調整將使粒子在兩個最優位置周圍進行搜索。

3 PSO-PCNN算法

PCNN的圖像濾波方法的處理過程是，首先對圖像中的噪聲像素進行精確定位，然后判別是否為噪聲像素，如果是有用信息，則根本不做處理，如果是噪聲，在對其進行類中值方法的濾波處理，這樣就能從根本上最大限度的保留住有用的信息像素，使圖像經過濾波后只能是向著原圖的方向漸漸靠攏，這樣在保持有用信息不被認為破壞的前提下，盡可能的濾除了噪聲污染，從而大大提高濾波性能［3］。

對于神經網絡優化，粒子群算法主要包括兩個方面：一是優化網絡各層之間的連接權值；二是對于網絡的拓撲結構進行優化。本章算法中確定的適應度函數可用原始訓練圖像和加噪濾波后的圖像的平均絕對誤差的倒數來表示：

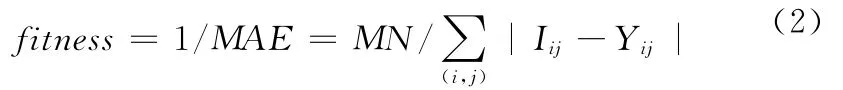
按照式（2），粒子群算法對PCNN模型參數自動確定的工作流程可表示如下：

1）隨機產生初始粒子群，即可用xi和vi分別表示第i個粒子的位置和速度；

2）通過激活PCNN神經網絡，根據粒子的位置對加噪圖像進行濾波，確定適應度，計算每個粒子的適應值fitness；

3）將第i個粒子適應值與該粒子曾經經歷過的自身最優位置pi的適應值作計算比較，如果其結果較好，則把該粒子當前對應的位置當作目前的最優位置pi；

4）將每個粒子當前的適應度與粒子群目前的全局最優位置pg的適應度作比較，計算結果如果較好，則將目前比較出的粒子對應的位置作為全局最優位置pg；

5）根據計算出的速度、位置的最新值更新公式（1）來改變粒子的速度和位置；

6）當優化終止條件（終止條件通常為足夠好的適應值或達到一個預設的足夠多的迭代次數）被滿足時，則輸出結果；否則返回第2步繼續循環，直到滿足終止條件為止。

4 仿真與實驗結果分析

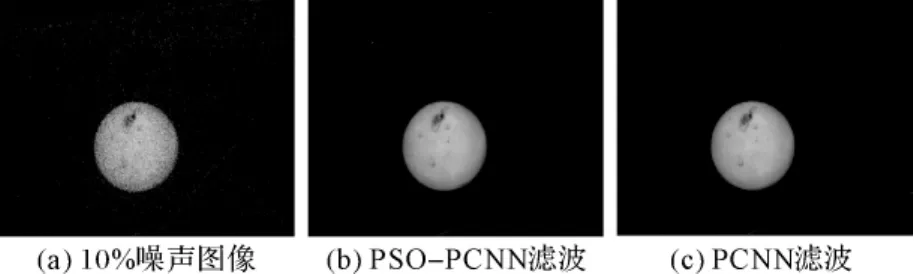
圖1 10%噪聲水下球體圖像的濾波結果比較

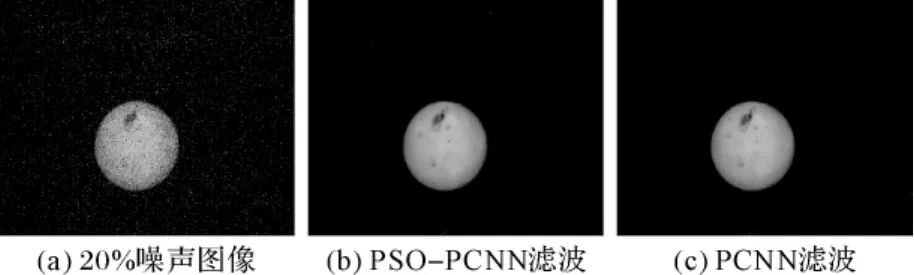
圖2 20%噪聲水下球體圖像的濾波結果比較

以水下球體圖像為例，分別在10%和20%噪聲強度下采用PSO-PCNN濾波和PCNN濾波，并對二者進行了比較。其仿真結果如圖1和圖2所示［4］。

根據上述算法，為了節省仿真時間，采用以下PSO參數：進化代數為2，種群中的粒子總數p＝10，權重因子w＝0.1，最大速度Vmax＝24.6。PSO在不同噪聲強度下對PCNN參數的自動確定數據如表1所示。

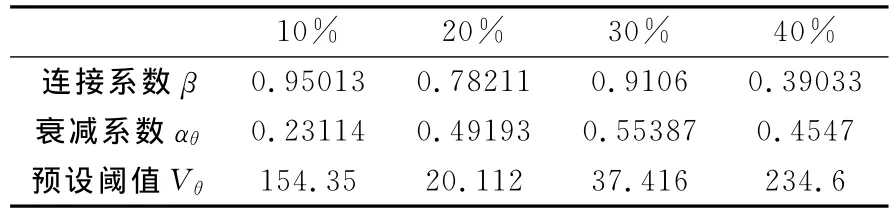
表1 PSO在不同噪聲下自動確定的PCNN參數

對水下球體圖像分別加10%、20%、30%和40%強度的噪聲，比較PSO-PCNN濾波和PCNN濾波的平均絕對誤差MAE的大小，如表2所示。

表2 對水下球體圖像加不同噪聲強度時采用兩種濾波方法的MAE性能比較

通過計算機仿真，從圖1和圖2中對兩種算法的濾波效果進行比較，可以得出這樣的結論：基于PSO的PCNN圖像濾波方法在去噪能力方面表現得比PCNN濾波方法要強一些，而且對PCNN模型中的參數也能夠很好的實現自動確定，不必手工設置PCNN參數。此外，從表1、表2的比較，也能夠得出：PSO-PCNN濾波方法比PCNN濾波的效果好得多。所以，總的看來，就濾波算法而言，PSOPCNN算法的濾波性能要優于PCNN濾波，能夠對PCNN模型中的參數實現自動確定，具有更強的適應性。

5 結語

在PCNN模型的參數需要反復試驗的前提下，提出了基于PSO的自動確定參數的PCNN圖像去噪算法。以水下球體圖像為例，加以不同程度的脈沖噪聲，將其與PCNN濾波進行比較；并對兩種算法的平均絕對誤差MAE的對比曲線進行仿真。結果表明，當噪聲密度在10%～40%之間時，PSO-PCNN濾波的平均絕對誤差明顯比PCNN法小得多，PSO-PCNN濾波比PCNN濾波方法的效果好［5］。

［1］孫小強，張求明.一種基于粒子群優化的多目標優化算法［J］.計算機工程與應用，2006（18）：40-42，78.

［2］鄭思平，陳紅周.一種加入創新粒子的粒子群［J］.數學理論與應用，2010（1）：14-17.

［3］邢杰，蕭德云.混合粒子群優化算法及其應用［J］.化工學報，2008（7）：1707-1710.

［4］王力維.基于粒子群優化算法的神經網絡鉆削參數優化［J］.科技信息（科學教研），2007（25）：344-538.

［5］張赫，徐玉如，萬磊，等.水下退化圖像處理方法［J］.天津大學學報，2010，43（9）：827-833.